Преобразование Лапласа и передаточные функции

В теории автоматического управления часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d /dt,так что, dy / dt = py, а pⁿ = dⁿ / dtⁿ. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p.

В теории автоматического управления широко применяется операторный метод описания линейных систем автоматического управления, использующий интегральное преобразование Лапласа (L – преобразование), имеющее следующий вид:

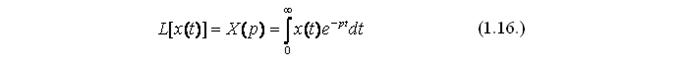
Данное преобразование называется прямым односторонним преобразованием Лапласа, преобразует функцию времени х(t) – оригинал, в функцию комплексной переменной

X (р) - изображение. Переменная р представляет собой комплексное число:

р = (a + jb) (1.17.)

где a, b - вещественные (действительные) части числа, j – мнимая единица.

Существует также обратный процесс перехода от изображения к оригиналу, называемый обратным преобразованием Лапласа (L^-1 – преобразование), имеющее следующий вид:

Существуют требования, являющиеся достаточными условиями, при которых возможно применение преобразования Лапласа:

- функция оригинала х(t) должна быть непрерывна и однозначна при всех t ≥ 0. Непрерывность может быть нарушена только в отдельных точках, которые являются точками разрыва непрерывности первого рода,

- функция оригинала х(t) = 0 для всех t < 0,

- функция оригинала х(t) должна иметь ограниченный порядок возрастания, т.е должны выполняться следующие условия: должны существовать постоянные a > 0, b > 0,

при которых х(t) < ае^bt, при t > 0.

Для часто применяющихся функций и облегчения применения преобразования Лапласа существуют таблицы, пример приведен на рисунке 23.

№ п/п	Вид функции (оригинал)	Изображение функции по Лапласу
1.	x(t)	X(p)
2.
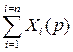
3.	A x(t)	A X(p)
4.	1(t)	1/p
5.	d(t)=1^’(t)
6.	d^i x(t)/dt^i, i=1…n	p^i X(p)
7.		X(p)/p
8.	x(t-t)	e^-p^t X(p)
9.	e^±^a^t	1/(p±a)
10.	(1/l) e^-^a^tSinlt	1/[(p+a)^2+l^2]
11.	(1/a)(1-e^-^a^t)	1/(p+a)p

Рис.23. Таблица преобразования по Лапласу наиболее часто встречающихся функций

Использование преобразования Лапласа дает возможность перейти от производных и интегралов к более простому алгебраическому выражению - функции комплексного переменного р. Используя преобразование Лапласа для дифференциального уравнения системы (1.14.) при нулевых начальных условиях, мы получим операторное описание системы в виде алгебраического уравнения:

Представив отношение изображения выходного параметра системы ко входному, получим передаточную функцию системы, которая не зависит от характера входного воздействия, а характеризует только собственные свойства системы. Данная функция имеет вид:

и в развернутом виде представляется, как:

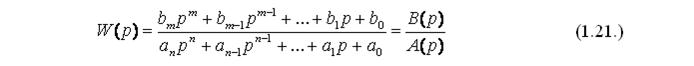
Следовательно, передаточной функцией называется отношение величины выходного параметра, к величине входного параметра, преобразованных по Лапласу, при нулевых начальных условиях.

Приравняв полином знаменателя передаточной функции к нулю, получим из первоначального дифференциального уравнения характеристическое уравнение системы:

Решение однородного дифференциального уравнения определяется корнями характеристического уравнения. Значение переменной р, при котором передаточная функция W(p)= 0, называется нулем, а значение, при котором W(p) = ∞ называется полюсом передаточной функции. Из (1.21.) следует, что нулями являются корни полинома B(p), а полюсами – корни полинома А(p).

Из выражения (1.20.) можно получить зависимость изображения по Лапласу выходной величины от изображения входной величины, которая будет иметь вид:

Первоначальное дифференциальное уравнение можно решить, применив к изображению выходной величины обратное преобразование Лапласа (1.18.), определив тем самым переходной процесс:

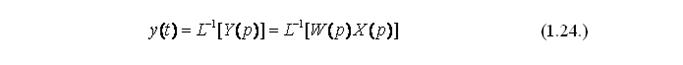
Применим к решению линейного дифференциального уравнения второго порядка, представленного ниже, преобразование Лапласа:

Для этого зададим начальные условия (значения y⁽¹⁾(t) и y(t) в начальный момент времени t = 0) и изменение во времени x(t). Примем нулевые начальные условия: y⁽¹⁾(0) = 0, y(0) = 0 и x(t) = 1 (t). С помощью таблицы (рисунок 23) преобразовав по Лапласу первоначальное дифференциальное уравнение, получаем: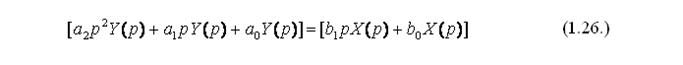

Вынесем за скобки Y (р) и X (р), и получим:

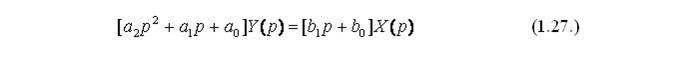
Используя таблицу (рисунок 23), находим X (p) = L [1 (t)] =1/ p и подставим данное значение в полученное уравнение, которое примет вид:

Решение уравнения относительно изображения выходной величины будет выглядеть таким образом:

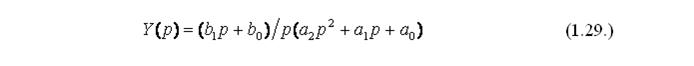
Для того, чтобы найти решение дифференциального уравнения, необходимо произвести операцию обратного преобразования Лапласа с изображением Y (р), поэтому для удобства пользования таблицей преобразования необходимо привести трехчлен, находящийся в знаменателе, к удобному виду. Для этого данный трехчлен необходимо разложить на множители:

в котором p ₁ и p ₂ — будут являться корнями уравнения

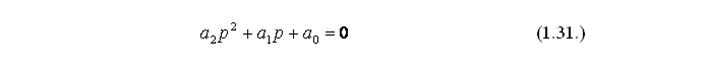
Получаем следующее выражение:

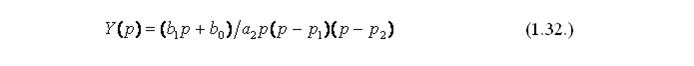
которое можно представить в виде суммы:

где С ₀, С ₁, С ₂ - коэффициенты, которые можно найти, решив тождественное уравнение, полученное путем сравнения числителя выражения (1.28.) и выражения (1.27.), деленного на а₂. Далее по таблице преобразования Лапласа (рисунок 23) найдем оригиналы для каждого слагаемого и получим следующее решение:

где С ₀, С ₁, С ₂ – коэффициенты, выступающие в качестве постоянных интегрирования, которые могут быть найдены по формулам начальных условий.

Пример применения преобразования Лапласа

Пусть система описывается следующим уравнением:

а₀ y ′′ + a₁ y ′ + a₂ y = k x (1.35.)

Необходимо найти передаточную функцию W(p) системы при

k = 1, а₀ = 1, a₁ = 3, a₂ = 2.

Решение:

Преобразуем уравнение системы с помощью преобразования Лапласа.

Получим следующее выражение:

(a₀ p² + a₁ p + a₂)Y (p) = kX (p) (1.36.)

Подставив имеющиеся числовые значения и преобразовав предыдущее выражение, получим значение передаточной функции, равное:

Задание выполнено.

Дата добавления: 2014-11-16