Інтерполяційний багаточлен Лагранжа

Найбільш загальною формулою параболічного інтерполювання є інтерполяційна формула Лагранжа. Задача параболічного інтерполювання в цьому випадку формулюється наступним чином: на відрізку у вузлах інтерполяції 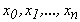задається функція 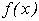своїми значеннями

,

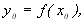
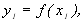
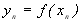необхідно побудувати багаточлен 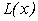так, щоб у вузлах інтерполяції 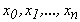його значення співпадали зі значеннями заданої функції, тобто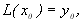 …, 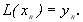Слід відзначити, що в такій постановці задачі вузли інтерполяції 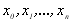можуть бути довільно розташовані один від одного на відрізку , іншими словами, вузли інтерполяції не рівновіддалені, тобто 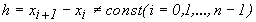. Величина називається кроком інтерполяції.

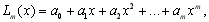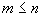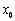Задача інтерполювання має розв‘язок, якщо степінь m багаточлена яким замінюється функція , не вище порядку (). Тоді задача інтерполювання зводиться до пошуку невідомих постійних коефіцієнтів багаточлена з системи рівнянь, яка будується наступним чином. З початкових умов відомо, що функція в вузлах приймає значення Тоді в вузлі інтерполяційний

багаточлен має вигляд 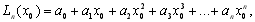в вузлі інтерполяції 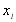- і так далі. Нарешті, в вузлі інтерполяційний багаточлен буде виглядати

.

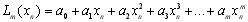Запишемо це у вигляді системи рівнянь з 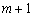невідомими

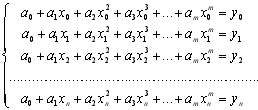, (5.3)

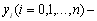де і табличні значення аргументу і функції, що досліджується. Невідомі коефіцієнти знаходяться по формулам Крамера:

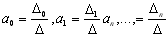, (5.4)

де - визначник системи (5.3).

Якщо (тобто коли різні), то система (5.3) має єдиний розв’язок. Якщо знайти коефіцієнти 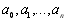, можна уявити інтерполяційний багаточлен у вигляді

Перепишемо багаточлен в іншій формі:

(5.5)

Легко перевірити, що функція 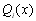повинна задовольняти умовам

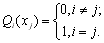
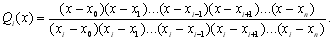(5.6)

В точках функція 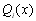обертається в 0, а в точці дорівнює 1.

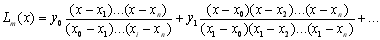
Остаточно отримаємо вираз 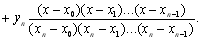(5.7)

(5.7)

Цей багаточлен називається інтерполяційним багаточленом Лагранжа. В спрощеному вигляді його можна записати так:

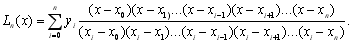(5.8)

Даний метод легко алгоритмізується і може використовуватися для розробки програм інтерполяції. Схема алгоритму метода представлена на рисунку 5.3.

Рисунок 5.3 – Схема алгоритму метода Лагранжа

Приклад: Побудувати інтерполяційний багаточлен Лагранжа для функції заданої таблично.

n
x
y

n=4; m=n-1=4-1=3. Припустимо, що y=a₀+a₁x+a₂x²+a₃x^{3 .}

Слід пам’ятати, що при екстраполяції функції, чим далі значення х від інтервалу спостереження, тим отримане значення функції містить більшу похибку.

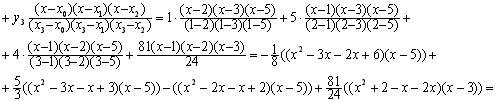
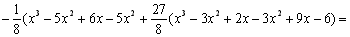
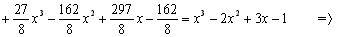
Таким чином: , , , .

Висновки:

1. Таким чином за допомогою багаточлена Лагранжа були отримані коефіцієнти інтерполяційної функції : .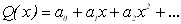

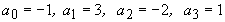2. Використовуючи отриманий багаточлен можливо знайти будь-яке значення функції для заданого 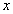. Наприклад, для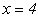

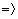
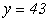
3. Використовуючи інтерполяційний багаточлен можливо отримати значення функції за межами спостережень. У даному прикладі інтервал спостереження 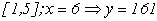. Така задача називається екстраполяція (прогнозування функції).

Для оцінки похибки інтерполяційного багаточлена Лагранжа використовують формулу:

,

причому , при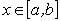

Дата добавления: 2014-11-08