Основы термодинамики. Термодинамическая система. Термодинамическое равновесие. Параметры состояния. Работа и теплота как формы обмена энергией между системами

.

1. Для функції 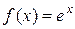маємо

і формула (10.21) набирає вигляду

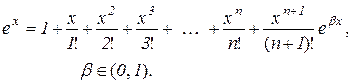(10.22)

2. Нехай 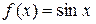, тоді

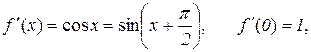
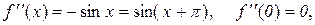
Таким чином,

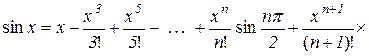
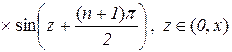. (10.23)

3. Аналогічно можна записати формулу (10.17) для функції :

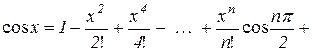
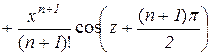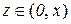, . (10.24)

Приклад 10.8. Обчислити 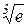з точністю до 0,001.

Розв’язування. Використаємо формулу (10.22) – розклад функції 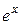за Маклореном. В нашому прикладі , тому залишковий член можна оцінити наступним чином

або

.

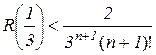Знайдемо n, при якому залишковий член не перевищує значення 0,001:

; ;

; .

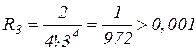Отже, в формулі Маклорена досить взяти п’ять перших доданків, щоб отримати значення 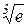з точністю до 0,001:

.

Запитання для самоконтролю.

1. Сформулюйте і доведіть теорему Ролля.

2. Дайте геометричне тлумачення теореми Ролля.

3. Сформулюйте й доведіть теорему Лагранжа.

4. Дайте геометричне тлумачення теореми Лагранжа.

5. Сформулюйте і доведіть теорему Коші.

6. Виведіть правило Лопіталя.

7. Які ви знаєте наслідки правила Лопіталя?

8. Як розкривати невизначеності типу , ?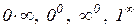

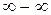9. Запишіть формули Тейлора і Маклорена.

10. Що таке залишковий член і форми його запису?

11. Запишіть формули Маклорена для функцій .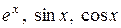

Приклади до розділу 10.

1. Показати, що між коренями функції 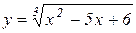міститься корінь її похідної.

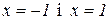2. Функція дорівнює нулю при . Показати, що на інтервалі її похідна не рівна нулю.

3. Перевірити справедливість формули Лагранжа для функції 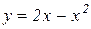на відрізку .

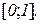4. Записати формулу Коші для функцій на відрізку і знайти с. Відп.: с=14/9.

5. Знайти границі:

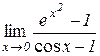а) Відп.: 2. б) . Відп.: – 2.

в) 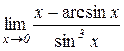. Відп.: – 1/6. г) 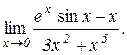. Відп.: 1/3.

д) 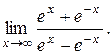. Відп.: 1. е) 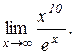. Відп.: 0.

6. Знайти границі:

а) 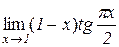. Відп.: 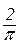. б) 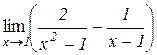. Відп.: .

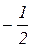в) 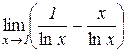. Відп.: –1. г) 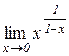. Відп.: .

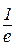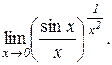д) . Відп.: 1. е) . Відп.: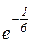

7. Розкласти за степенями двочлена 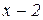многочлен

.

8. Записати формулу Маклорена для функції , якщо .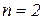

9. Знайти 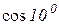з точністю до 0,001.

Дата добавления: 2014-11-18