Развертка поверхности призмы

Развертка поверхностей многогранников

Построение разверток

Разверткой поверхности называется плоская фигура, образованная последовательным совмещением поверхности с плоскостью без разрывов и складок. При развертывании поверхность рассматривается как плоская, но нерастяжимая. Цель развертывания поверхностей – создание моделей поверхностей из листового материала путем последующего изгибания и «свертывания» их разверток.

Основные свойства разверток:

- прямая на поверхности переходит в прямую на развертке;

- параллельные прямые на поверхности переходят в параллельные прямые на развертке;

- длины отрезка линии на поверхности и той же линии на развертке равны;

- углы между линиями на поверхности и между соответствующими линиями на развертке равны;

- площадь развертки равна площади поверхности;

- все размеры на развертке имеют натуральную величину.

Все поверхности подразделяются на развертываемые и неразвертываемые.

К развертываемым поверхностям относятся:

- гранные поверхности (пирамиды, призмы и т.д.), т.к. плоские элементы многогранника точно совмещаются с плоскостью развертки. В этом случае развертка называется точной.

- линейчатые поверхности (цилиндрические, конические и поверхности с ребром возврата), т.е. это поверхности, у которых смежные образующие-прямые параллельны или пересекаются.

К неразвертывающимся поверхностям относятся все остальные линейчатые, а также нелинейчатые поверхности (цилиндроиды, коноиды, сфера). Развертки этих поверхностей в этом случае называются приближенными или условными.

При построении разверток многогранников определяют натуральную величину всех его граней (плоских многоугольников). При этом используют различные способы преобразования чертежа. Выбор тех или иных способов зависит от вида многогранника и его расположения относительно плоскостей проекций.

Существует два способа развертки призмы: способ «нормального сечения» и способ «раскатки».

Способ «нормального сечения» используют для развертки поверхности призм общего положения. В этом случае строится нормальное сечение призмы (т.е. вводится плоскость, расположенная перпендикулярно боковым ребрам призмы) и определяются натуральные величины сторон многоугольника этого нормального сечения.

Пример выполнения развертки трехгранной призмы общего положения способом «нормального сечения» рассмотрим в задаче согласно рисунка 1.5.1

Обратим внимание на то, что в нашем случае боковые ребра призмы являются фронталями, т.е. на плоскость П₂ они проецируются в натуральную величину.

Решение:

1) Во фронтальной плоскости проекций построим фронтально проецирующую плоскость γ(γ ₁), которая одновременно перпендикулярна боковым ребрам призмы AD, CF, BE. Полученное нормальное сечение выразится в виде треугольника 123. Методом плоско-параллельного перемещения определим его натуральную величину в соответствии с рисунком 1.5.2.

2) Все стороны нормального сечения последовательно отложим на прямой: 1₀2₀=1₁¹2₁¹; 2₀3₀=2₁¹3₁¹; 3₀1₀=3₁¹1₁¹.

3) Через точки 1₀,2₀,3₀ проведем прямые, перпендикулярные прямой 1₀-1₀ и отложим на них натуральную величину боковых ребер: 1₀D₀ =1₂D₂ и 1₀A₀ = 1₂A₂; 2₀F₀ = 2₂F₂ и 2₀C₀ = 2₂C₂; 3₀E₀ = 3₂E₂ и 3₀B₀ = 3₂B₂.

4) Полученные точки верхнего и нижнего оснований призмы соединим прямыми A₀B₀C₀ и D₀F₀E₀. Плоская фигура A₀B₀C₀D₀F₀E₀ является искомой разверткой боковой поверхности данной призмы. Для построения полной развертки необходимо к развертке боковой поверхности пристроить натуральные величины оснований. Для этого воспользуемся полученными на развертке натуральными величинами их сторон A₀C₀, C₀B₀, B₀A₀ и D₀F₀, F₀E₀, E₀D₀ в соответствии с рисунком 1.5.3

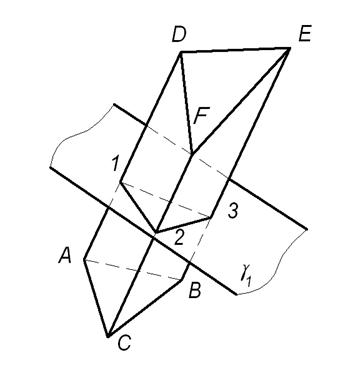
Рисунок 1.5.1

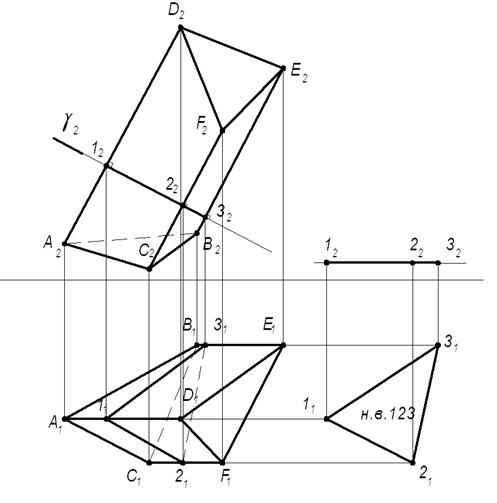
Рисунок 1.5.2

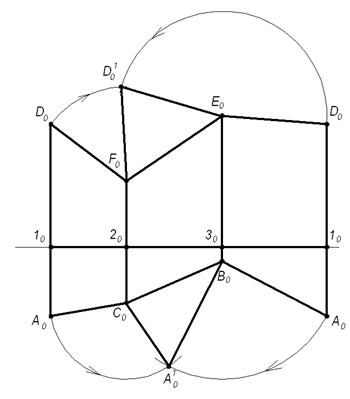
Рисунок 1.5.3 – Развертка призмы способом «нормального сечения»

Способ «раскатки». Этот способ удобен для построения разверток призм с основанием, лежащим в плоскости уровня. Суть способа заключается в последовательном совмещением боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы (рисунок 1.5.4).

Этим способом построена развертка поверхности призмы ABCDEF, боковые ребра которой являются фронталями, а нижнее основание лежит в горизонтальной плоскости (рисунок 1.5.5).

Решение:

1) Боковые грани призмы совместим с фронтальной плоскостью, проходящей через ребро AD. Это удобно в этом случае, т.к. фронтальные проекции боковых ребер призмы равны их истинной длине. Тогда ребро A₀D₀ развертки будет совпадать с фронтальной проекцией ребра AD(A₂D₂).

2) Для определения на развертке истиной величины боковой грани ADEB вращаем ее вокруг ребра AD до положения, параллельного фронтальной плоскости проекций. Чтобы определить на развертке положение точки B₀, из точки B₂ восстанавливаем перпендикуляр к A₂D₂. Точка B₀ будет найдена в пересечении этого перпендикуляра с дугой окружности радиуса R₁, равного истиной величине ребра AB и проведенной из точки A₂, как из центра.

3) Точка E₀ будет определяться на развертке как результат пересечения прямой B₀E₀ параллельной фронтальной проекцией ребра BE(B₂E₂), и перпендикуляра, восстановленного из точки E₂ к A₂D₂.

4) Точки C₀ и A₀ построены аналогично точке B₀ в пересечении перпендикуляров из точек C₂ и A₂ к фронтальным проекциям ребер, с дугами окружностей, проведенных из точек B₀ и C₀ как из центров радиусами R₂ и R₃, равными соответственно ребрам BC и CA. Точки F₀ и D₀ определяются аналогично точке E₀.

5) Соединив последовательно совмещенные вершины ломаными линиями, получим развертку боковой поверхности призмы A₀B₀C₀A₀D₀F₀E₀D₀. При необходимости можно получить полную развертку призмы, присоединив к ней натуральные величины обоих оснований.

Если боковые ребра призмы занимают общее положение, то предварительным преобразованием чертежа их надо привести в положение линий уровня.

Рисунок 1.5.4 – Способ «раскатки»

Рисунок 1.5.5 – Развертка боковой поверхности призмы способом «раскатки»

Дата добавления: 2014-11-18