Двойные интегралы в полярных координатах

Замена переменных в двойных интегралах.

Литература: [3, №№ 3525 - 3531, 3559 - 3588; 5, гл. 2, §§ 2.6 - 2.8; 6, гл. 1, § 6].

Рассмотрим функции

{u=φ(x,y), v=ψ(x,y)}єС’(Ω) (6.2.17)

где через Ω обозначено множество точек плоскости OXY. Допустим, что уравнения (6.2.17) решены относительно х и у:

{x=φ₁(u,v), y=ψ₁(u,v)}єС’(Ω₁) (6.2.17)

где Ω₁ - множество точек плоскости Ouv. Каждой точке (u, v) соответствует точка (х, у). Пусть u = const, v = var. Тогда функции х = φ₁(v), у = ψ₁(v) зада­ют параметрически некоторые линии на плоскости Оху. Аналогично при v = const, и = var имеем линии х = φ₂(u), у = ψ₂(u), которые называются криволи­нейными координатами, а величины (u,v) являются криволинейными коор­динатами. Рассмотрим полярную систему координат (р,φ). Здесь u = р, v = φ: х = pcosφ; у = psinφ. Пусть р = const. Тогда координатные линии - ок­ружности:

x² + y² = ρ² (cos²φ + sin²φ) = R².

при φ = const координатными линиями являются полярные лучи (рис.6.2.6).

Можно показать, что функции (6.2.17), (6.2.18) взаимно-однозначно отображают области D_xy и D_uv и

, (6.2.19)

где I(u, v) - функциональный определитель, который называется якобианом преобразования (по имени математика Якоби):

. (6.2.20)

Для полярной системы координат

.

Тогда

, (6.2.20)

- двойной интеграл в полярных координатах. Так как двойной интеграл не зависит от способа разбиения области D на элементы Di, разобьем область D координатными линиями р = const, φ = const (см. рис.6.2.6). Площадь эле­мента

Составляя интегральную сумму и переходя к пределу при n→∞, max diam(ΔSi) → 0, получаем Δφ_i→dφ, Δp_i→dp: l/2(p_i+1 + p_i) → p; dS →ρdρdφ - дифференциал элемента площади в полярных координатах. То­гда двойной интеграл принимает вид (6.2.20). Область D в полярной системе координат называется правильной в направлении луча φ=const, если этот луч, проведенный через любую внутреннюю точку области, пересечет её границу только в двух точках (например, см. рис. 6.2.6). Двойной интеграл в полярной системе координат вычисляется путем сведения его к повторному. Если область D ограничена лучами φ₁ = α, φ₂ = β, разбивающими границу области на линии ρ =ρ₁(φ) и ρ =ρ₂(φ) (см. рис. 6.2.6), то

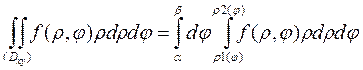, (6.2.21)

где ρ₁(φ) -"входящая" линия, ρ₂(φ) -"выходящая" линия в направлении луча
φ = const, который проходит через внутреннюю часть области D.

Порядок интегрирования в полярной системе координат меняют так: огра­
ничим область интегрирования D дугами окружностей ρ₁ = const и ρ₂ -
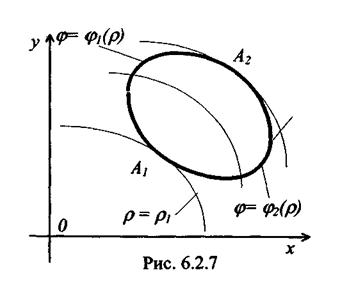
const, разбивающими границу области D на линии: φ = φ₁(ρ) и φ = φ₂(ρ) (рис. 6.2.7). Тогда

. (6.2.22)

Замечание 1. Если область D неправильная по φ = const, то разбиваем её на ряд правильных областей и пользуемся свойством 3.

Замечание 2. Если линии ρ₁(φ) и ρ₂(φ) состоят из различных ли­ний, то промежуток α≤φ≤β также разбиваем линиями φ = const на ряд об­ластей D_к и вновь используем свойство 3.

Пример 6.2.3. Записать двойной интеграл по области D в полярной системе координат и вычислить его:

.

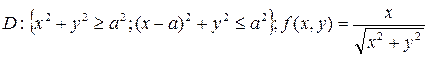Решение. Запишем уравнения окружностей в полярной системе коор­динат:

х² + у² = р² = а² => ρ₁ = а; (х - а)² + у² =а² => х² + у² = 2ах => ρ₂ = 2acosφ.

Найдем пределы интегрирования (рис. 6.2.8). Решая систему уравнений ρ₁=a, ρ₂ = 2аcosφ, находим а=2аcosφ => φ_1,2 = ±π/3, то есть α = -π/3, β = π/3. Очевидно, что уравнение "входящей" линии ρ = ρ₁(φ) - а, "выходящей" - ρ = ρ₂(φ) = 2acosφ.

Тогда

;

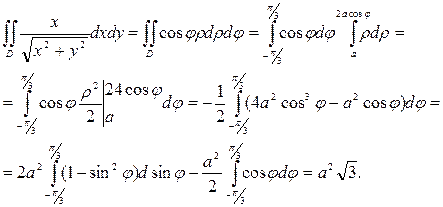
6.2.5. Вычисление объёмов тел с помощью двойного интеграла

Литература: [3, №№ 3580 - 3596; 5, гл. 2, § 2.12; 6, гл. 1, § 4].

Установлено (подразд. 6.2.1), что объём цилиндрического тела, огра­ниченного поверхностями z= 0, z =f(х,у) >0 и боковой поверхностью ци­линдра, равен

.

Если в области D существуют подобласти D_k (k=l,...,n), где f(x,y)≤0, то объём тела

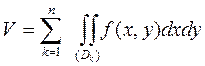. (6.2.23)

Если вычислить интеграл, не учитывая знаки модуля, то он будет равен разнице объёмов тел, расположенных выше и ниже плоскости координат 0XY. Если же тело ограничено сверху и снизу поверхностями z₁ =f₁(x,y) и z₂ = f₂(х,у) так, что f₂(x,y)≥f₁(x,y): (x,y)є(D), где D - проекция поверхно­стей z₁ и z₂ на координатную плоскость (например ОXY), то объём замкну­того тела

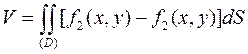, (6.2.24)

где V₁ и V₂ - объёмы цилиндрических тел, ограниченных поверхностями V₁: {z = 0; z₁ =f₁(x,y)}; V₂: {z = 0; z₂=f₂(x,y)}. Формула (6.2.24) справедлива, если в области D функции z₁ и z₂ прини­мают и отрицательные значения, но так, чтобы z₂ ≥ z₁.

Иногда необходимо вычислить объём цилиндрического тела, обра­зующие которого перпендикулярны координатной плоскости 0YZ (или 0XZ. Тогда цилиндр ограничивают поверхностями x = φ(y,z), x = 0 я объём вычис­ляется по формуле

. (6.2.25)

Пример 6.2.4. Найти объём тела, ограниченного поверхностями V: {z = 9 - х²; х=0; у=0; z=0; Зх + 4у = 12; у≥0}. Поверхность z = 9 - у² - ци­линдр; х = 0; у = 0; z = 0 - координатные плоскости; 3х + 4у = 12 - плос­кость, параллельная оси Oz, оставляющая на плоскости 0XY след с тем же уравнением.

Решение. Рассмотрим один из вариантов решения этой задачи. Пусть область V проектируется цилиндром z = 9 – у² и плоскостями у = 0, z = 0 на координатную плоскость 0YZ в область D_yz: {0≤у≤3; 0≤z≤9-у²}. По­дынтегральная функция в выражении (6.2.25) φ(у, z): х- 4 - 4у/3. Тогда

Дата добавления: 2014-11-20