Вычисление тройных интегралов в декартовой системе координат

Литература: [3, №№3547 – 3551; 5, гл. 2, §§ 2.4; 6, гл.2, §3].

Если разбить область V плоскостями, параллельными координатным плоскостям, то ΔV_i = Δx_i Δy_i Δz_i, что после предельного перехода дает элемент объема в декартовой системе координат dV=dxdydz. Спроектируем тело цилиндрической поверхностью на плоскость. Цилиндр касается тела вдоль некоторой линии L, которая разделяет ограничивающую поверхность z=f(x,y) на нижнюю z_l=f_l(x,y) («входящая» поверхность) и верхнюю z₂=f₂(x,y) («выходящая» поверхность) части (рис. 6.3.1). Вычислим интеграл от функции f(x,y,z) вдоль оси OZ от точки А до точки В. Тогда координаты z точки меняются от z_l=f_l(x,y) до z₂=f₂(x,y):

Очевидно, здесь х и у считаются постоянными. Итак, тройной интеграл может быть представлен в виде

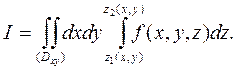
Если внешний двойной интеграл по области D_xy привести к повторному в соответствии с разд. 6.2, то получим

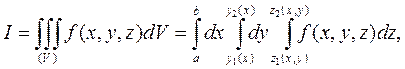(6.3.2)

где y₁(x), y₂(x) - уравнения «входящих» и «выходящих» линий области D_xy.

Если область V правильная в направлении оси ОХ, то, проектируя тело на плоскость OYZ в область D_yz и записывая уравнения «входящей» и «выходящей» поверхностей в виде x_l=x_l(y,z); x₂=x₂(y,z), получим

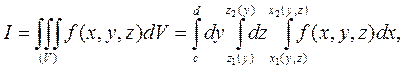(6.3.3)

Аналогично для правильной области V в направлении оси OY

(6.3.4)

Если поверхность, ограничивающая тело, состоит из разных поверхностей, то область V разбивают так, чтобы в пределах каждой области поверхности задавались одним аналитическим выражением.

Пример 6.3.1. Расставить пределы интегрирования в тройном интеграле различными способами: V: {z²≥x²+y²; 2-z≥x²+y²}.

Решение. Данная область является правильной в направлении всех осей (рис. 6.3.2).

1. Пусть тело проектируется на плоскость OXY в виде фигуры D_xy, тогда «входящая» поверхность – конус z² = x² + y², а «выходящая» - параболоид z = 2 - x^{2 -} y². Область D_xy - круг. Исключая из уравнений поверхностей x² + y² получаем z₂ +z – 2 = 0 → z_1,2 = = (1, -2).

Линия пересечения поверхностей данной задачи лежит в плоскости z₁ = 1и представляет собой окружность x² + y² = 1.

Тогда

2. Пусть область проектируется на плоскость OYZ в фигуру D_yz (см. рис. 6.3.2). «Входящая» и «выходящая» поверхности на промежутке 0≤z≤2 состоят из поверхностей конуса и параболоида.

Разобьем область V плоскостью z = 1 на V₁ и V₂, которые проектируются на плоскость OYZ в виде фигуры D⁽¹⁾_yz и D⁽²⁾_yz соответственно. Тогда I = I_v1 + I_v2. Для области V₁ «входящая» поверхность - 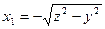(конус), «выходящая» - (конус). Тогда

Для области V₂ «входящая» поверхность - (параболоид), «выходящая» - (параболоид)

Пример 6.3.2. Вычислить интеграл по области V, ограниченной поверхностями 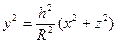(конус) и y=h (плоскость) (рис. 6.3.3).

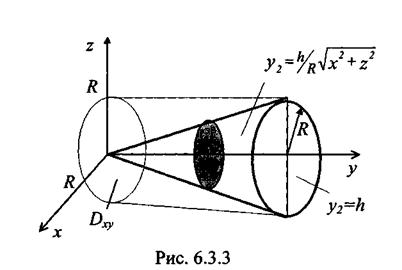Решение. Область проектируется на плоскость OXZ в круг 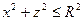, так как в сечении y=h:

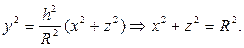
Тогда «входящая» поверхность в направлении оси OY - конус 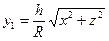, а «выходящая» - плоскость y=h. Получаем последовательно:

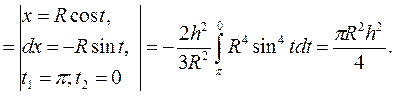
Дата добавления: 2014-11-20