Свойства криволинейных интегралов второго рода

Криволинейные интегралы второго рода

Литература: [3, №№3806 – 3821, 3861 – 3868; 5, гл. 3, § 3.3; 6, гл.4, §2; 20, гл. 2, § 5].

Пусть гладкая ориентированная кривая Г задана уравнением (6.4.1). Тогда

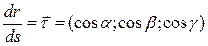(6.4.9)

- единичный вектор касательной к этой кривой. Здесь α, β, γ - углы, образованные касательной с координатными осями OX, OY, OZ соответственно.

Если на кривой Г определена вектор-функция F = (P; Q; R), такая, что для скалярной функции F_τ = (F, τ) = Pcosα + Qcosβ + Rcosγ существует

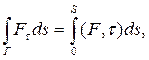(6.4.10)

то данный интеграл называют криволинейным интегралом второго рода (по координатам) от функции F по кривой Г и обозначают . Таким образом, по определению

(6.4.11)

1. При изменении ориентации кривой на противоположную криволинейный интеграл второго рода изменяет знак.

2. Если гладкая кривая Г задана уравнением (6.4.4.), а вектор-функция F=(P;Q;R) непрерывна на Г, то

(6.4.12)

В случае, когда Г – плоская гладкая кривая, заданная уравнением (6.4.6), из формулы (6.4.11) следует:

(6.4.13)

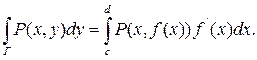(6.4.14)

Пример 6.4.2. Вычислить криволинейный интеграл 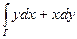по кривой Г с начала в т.О(0;0) и концом в т.А(1;1), если (рис. 6.4.2): 1) Г – отрезок ОА; 2) Г – дуга параболы y = x²; 3) Г – дуга окружности радиусом 1 и с центром в точке (1;0).

Так как отрезок ОА задается уравнением y = x, 0 ≤ y ≤ 1, то, пользуясь формулами (6.4.13) и (6.4.14), находим:

1.

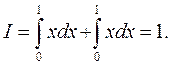
2. Если Г – дуга параболы, то .

3. Так как уравнение дуги окружности записывается в виде x = 1 + cost, y = sint, где t є [π;π/2], то по формуле (6.4.12) получаем

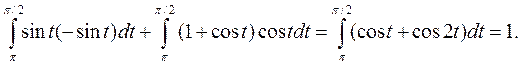
Дата добавления: 2014-11-20