ЛЕКЦИЯ 4. Арифметические основы компьютеров

Вопросы для самоконтроля

3.1. По каким признакам можно разделять компьютеры на классы и виды?

3.2. Как эволюционировала элементная база компьютеров от поколения к поколению?

3.3. В какой последовательности возникали известные Вам языки программирования?

3.4. Когда микрокомпьютеры стали доступны для широкого домашнего применения?

3.5. Можете ли Вы связать понятия "яблоко", "гараж" и "компьютер"?

3.6. На основе каких технических элементов создавались компьютеры первого поколения?

3.7. Какую основную проблему перед разработчиками и пользователями выдвинул опыт эксплуатации компьютеров первого поколения?

3.8. Какая элементная база характерна для второго поколения компьютеров?

3.9. Какую функцию выполняет операционная система в процессе работы компьютера?

3.10. На какой элементной базе конструируются машины третьего поколения?

3.11. Из каких основных этапов состоит процесс изготовления микросхем?

3.12. Для каких поколений компьютеров характерно широкое использование интегральных схем?

3.13. Какое быстродействие характерно для машин четвёртого поколения?

3.14. Что подразумевают под "интеллектуальностью" компьютеров?

3.15. Какую задачу должен решать "интеллектуальный интерфейс" в машинах пятого поколения?

3.16. Какими особенностями должны обладать промышленные компьютеры?

3.17. Что такое операторский компьютерный интерфейс?

3.18. По каким основным признакам можно отличить мэйнфреймы от других современных компьютеров?

3.19. На какое количество пользователей рассчитаны мэйнфреймы?

3.20. Какие идеи лежат в основе архитектуры суперкомпьютеров?

3.21. На каких типах задач максимально реализуются возможности суперкомпьютеров?

3.22. Какие свойства и конструктивные особенности отличают векторные процессоры?

3.23. Назовите основные характеристики какого-либо суперкомпьютера.

3.24. Что означают в переводе на русский язык названия Laptop, Notebook, Palmtop?

3.25. Как в Palmtop компенсируется отсутствие накопителей на дисках?

4.1. Что такое система счисления?

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7 ^. 10² + 5 ^. 10¹ + 7 ^. 10⁰ + 7 ^. 10^—1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1 q^n-1 + a_n-2 q^n-2 +... + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 +... + a_-m q^-m,

где a_i — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно.
Например:

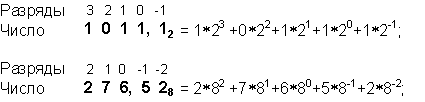
4.2. Как порождаются целые числа в позиционных системах счисления?

В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.

Продвижением цифры называют замену её следующей по величине.

Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.

Целые числа в любой системе счисления порождаются с помощью Правила счета [44]:

Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.

Применяя это правило, запишем первые десять целых чисел

• в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
• в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
• в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
• в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

4.3. Какие системы счисления используют специалисты для общения с компьютером?

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

• двоичная (используются цифры 0, 1);
• восьмеричная (используются цифры 0, 1,..., 7);
• шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1,..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).

Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:

10-я	2-я	8-я	16-я

10-я	2-я	8-я	16-я
			A
			B
			C
			D
			E
			F

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.

4.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной?

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
• представление информации посредством только двух состояний надежно и помехоустойчиво;
• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
• двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

4.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

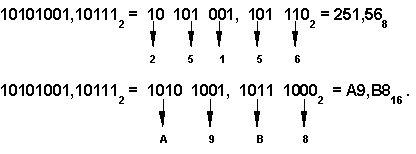
4.6. Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q, записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q, и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q -ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

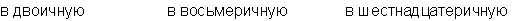
Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

4.7. Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?

Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q -ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q -ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q ^-(k+1) / 2.

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.

4.8. Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную?

Перевод в десятичную систему числа x, записанного в q -ичной cистеме счисления (q = 2, 8 или 16) в виде x_q = (a_na_n-1 ... a₀ , a_-1 a_-2... a_-m)_q сводится к вычислению значения многочлена x₁₀ = a_n qⁿ + a_n-1 q^n-1 +... + a₀ q⁰ + a_-1 q ^-1 + a_-2 q^-2 +... + a_-m q^-m средствами десятичной арифметики.

Примеpы:

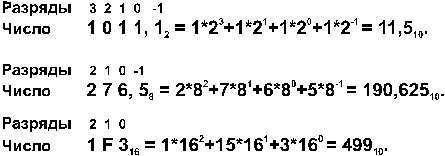
Дата добавления: 2014-11-08