
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример выполнения работы № 4
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 4
«Решение дифференциальных уравнений»
Цель работы: Научить студентов решать дифференциальные уравнения с использованием прикладных математических пакетов MAPLE.
Задания
1. Найти общее решение или общий интеграл дифференциального уравнения.
2. Найти общее решение или общий интеграл дифференциального уравнения.
3. Найти решение задачи Коши для заданного уравнения и построить график интегральной кривой.
4. Найти общее решение дифференциального уравнения.
Варианты заданий
Вариант 1 Вариант 2
1. 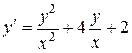 . 1.
. 1. 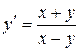 .
.
2. 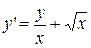 . 2.
. 2. 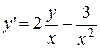 .
.
3. 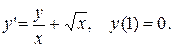 3.
3. 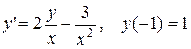 .
.
4. 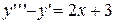 . 4.
. 4. 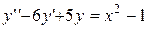 .
.
Вариант 3 Вариант 4
1. 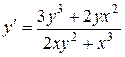 . 1.
. 1. 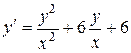 .
.
2. 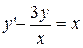 . 2.
. 2. 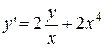 .
.
3. 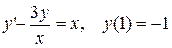 . 3.
. 3. 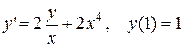 .
.
4. 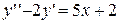 . 4.
. 4.  .
.
Вариант 5 Вариант 6
1. 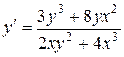 . 1.
. 1. 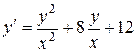 .
.
2. 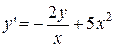 . 2.
. 2. 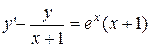 .
.
3. 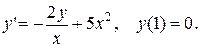 3.
3. 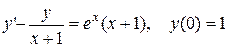 .
.
4. 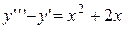 . 4.
. 4. 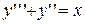 .
.
Вариант 7 Вариант 8
1. 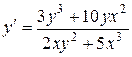 . 1.
. 1. 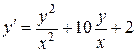 .
.
2. 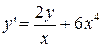 . 2.
. 2. 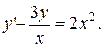
3. 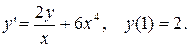 3.
3. 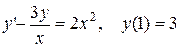 .
.
4. 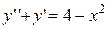 . 4.
. 4. 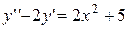 .
.
Вариант 9 Вариант 10
1. 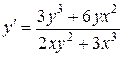 . 1.
. 1. 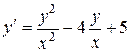 .
.
2. 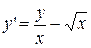 . 2.
. 2. 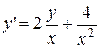 .
.
3. 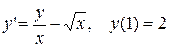 . 3.
. 3. 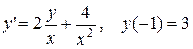 .
.
4. 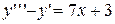 . 4.
. 4. 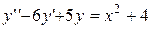 .
.
Вариант 11 Вариант 12
1. 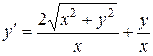 . 1.
. 1. 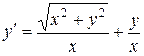 .
.
2.  . 2.
. 2. 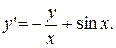
3. 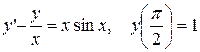 . 3.
. 3. 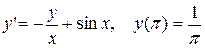 .
.
4. 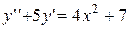 . 4.
. 4. 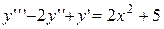 .
.
Вариант 13 Вариант 14
1.  . 1.
. 1. 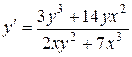 .
.
2. 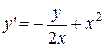 . 2.
. 2. 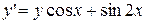 .
.
3. 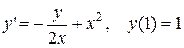 . 3.
. 3. 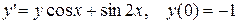 .
.
4. 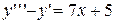 . 4.
. 4. 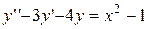 .
.
Вариант 15 Вариант 16
1. 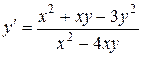 . 1.
. 1. 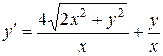 .
.
2. 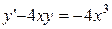 . 2.
. 2. 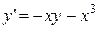 .
.
3. 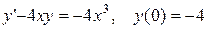 . 3.
. 3. 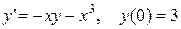 .
.
4. 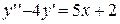 . 4.
. 4. 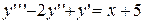 .
.
Вариант 17 Вариант 18
1. 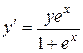 . 1.
. 1. 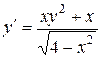 .
.
2. 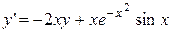 . 2.
. 2. 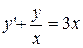 .
.
3. 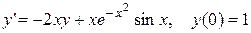 . 3.
. 3.  .
.
4. 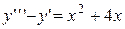 . 4.
. 4. 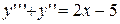 .
.
Вариант 19 Вариант 20
1.  . 1.
. 1. 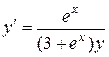 .
.
2. 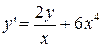 . 2.
. 2. 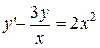 .
.
3. 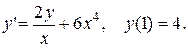 3.
3. 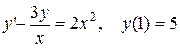 .
.
4. 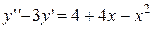 . 4.
. 4. 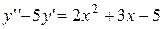 .
.
Вариант 21 Вариант 22
1. 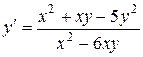 . 1.
. 1. 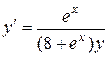 .
.
2. 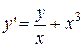 . 2.
. 2. 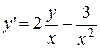 .
.
3. 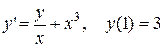 . 3.
. 3. 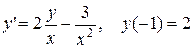 .
.
4. 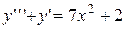 . 4.
. 4.  .
.
Вариант 23 Вариант 24
1. 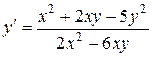 . 1.
. 1. 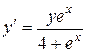 .
.
2. 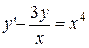 . 2.
. 2. 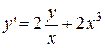 .
.
3. 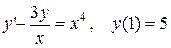 . 3.
. 3. 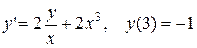 .
.
4. 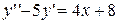 . 4.
. 4.  .
.
Вариант 25 Вариант 26
1. 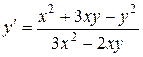 . 1.
. 1. 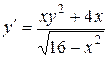 .
.
2. 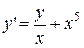 . 2.
. 2. 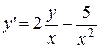 .
.
3. 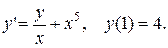 3.
3. 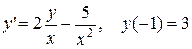 .
.
4. 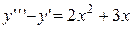 . 4.
. 4. 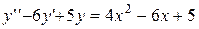 .
.
1. Найти общее решение или общий интеграл дифференциального уравнения
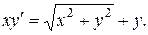
Введем дифференциальное уравнение
> de:= x*diff(y(x),x)=sqrt(x^2+(y(x))^2)+y(x);
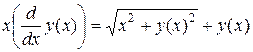
Находим общий интеграл дифференциального уравнения
> dsolve(de,y(x));
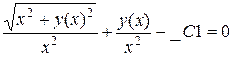
2. Найти решение задачи Коши и построить график интегральной кривой
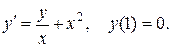
Введем дифференциальное уравнение
> de:=diff(y(x),x)-y(x)/x-x^2;
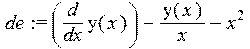
Записываем начальное условие и решаем задачу Коши.
> ic:=y(1)=0;dsolve({de,ic},y(x));
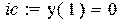

|
|
|
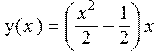
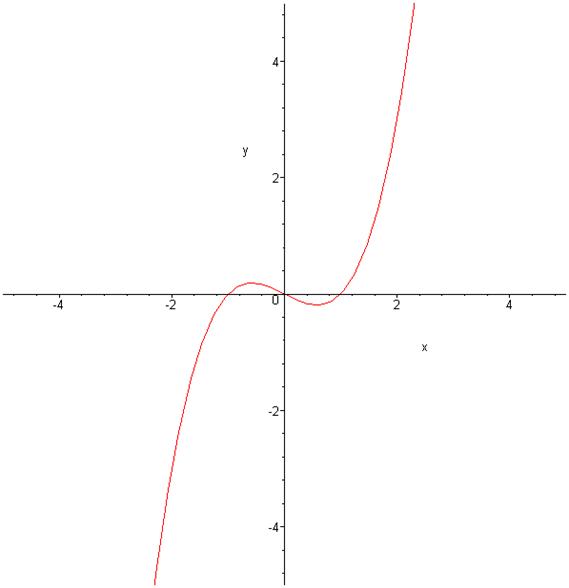
Строим найденную интегральную кривую
> plot((1/2*x^2-1/2)*x,x=-5..5,y=-5..5);
3. Найти общее решение дифференциального уравнения
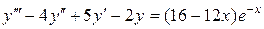
Введем дифференциальное уравнение
> de:=(D@@3)(y)(x)-4*(D@@2)(y)(x)+5*D(y)(x)-2*y(x)-(16-12*x)*exp(-x);
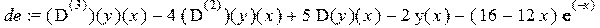
Находим общее решение и упростим полученное выражение
> simplify(dsolve(de,y(x)));
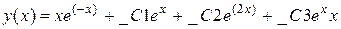 .
.
Контрольные вопросы
1. Что называется дифференциальным уравнением? Что называется порядком дифференциального уравнения?
2. Что называется частным, общим решением дифференциального уравнения 1-го порядка? Что называется частным, общим интегралом дифференциального уравнения 1-го порядка?
3. Как формулируется задача Коши для дифференциального уравнения первого порядка?
4. Какие типы дифференциальных уравнений 1-го порядка Вы знаете?
5. Как решаются дифференциальные уравнения с разделяющимися переменными?
6. Что называется линейным уравнением 1-го порядка? Какие методы их решения Вы знаете?
7. Как решаются однородные уравнения 1-го порядка?
8. Что называется частным, общим решением дифференциального уравнения n-го порядка? Что называется частным, общим интегралом дифференциального уравнения n-го порядка?
9. Как ставится задача Коши для дифференциального уравнения n-го порядка?
10. Какие виды уравнений высших порядков, допускающих понижение порядка, Вы знаете?
11. Сформулируйте понятие линейного уравнения n-го порядка.
12. Как выписывается определитель Вронского? Сформулируйте признак линейной независимости системы решений линейного однородного уравнения n-го порядка.
13. Что называется фундаментальной системой решений линейного однородного уравнения n-го порядка?
14. Структура общего решения линейного однородного уравнения n-го порядка.
15. Структура общего решения линейного неоднородного уравнения n-го порядка.
16. Что такое характеристическое уравнение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами?
|
|
|
17. Как находится общее решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами?
18. Сформулируйте методы нахождения частного решения линейного неоднородного дифференциального уравнения n-го порядка с постоянными коэффициентами?
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 454; Нарушение авторских прав?; Мы поможем в написании вашей работы!