Ядерная модель атома. Формула резерфорда. 3 страница

2) Электроны запускаются потоком с малым временем экспозиции.

Результаты эксперимента оказались одинаковыми в том и другом случае, при этом весьма парадоксальными. Если закрыть одну из щелей, то на экране будет один из максимумов. Теоретически, для двух щелей ожидалось увидеть картину двух максимумов:

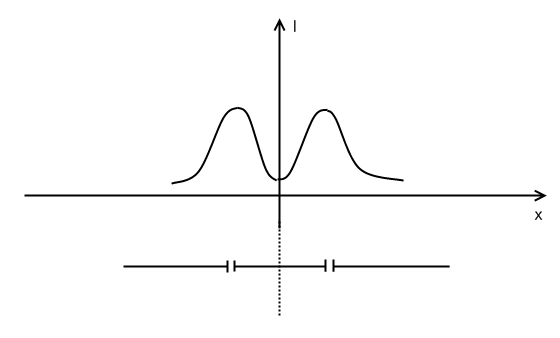
На опыте была зарегистрирована картина, аналогичная интерференции света:

Если считать, что электрон проходит через какую-то одну щель, то наличие интерференционной картины наводит на мысль, что электрон каким-то образом ощущает вторую щель, иначе ему было бы безразлично состояние второй щели, и в этом случае наблюдалась бы корпускулярная сумма интенсивностей.

Т.о., на характер интерференционной картины, а значит и на движение электрона влияют обе щели! Этот вывод несовместим с классическими представлениями о том, что электрон движется по какой-то траектории (если бы это было так, то электрон двигался бы только через одну определенную щель, однако электрон не можем одновременно проходить через две щели, т.к. это элементарная частица, которую невозможно расщепить).

Вывод: микрочастицу нельзя представлять, как классическую м.т., движущуюся по определенной траектории.

В случае опыта с регистрирующими электроны устройствами возле каждой щели было установлено, что всегда срабатывает счетчик только одной щели, т.е. электрон действительно не расщепляется. Однако в этом опыте электрон начинает вести себя, как корпускула и интерференционная картина не наблюдается.

Вывод: наблюдение за микрочастице изменяет ее состояние.

Наблюдение интерференции и дифракции электронов позволило М.Борну в 1926г. Предложить статистическую интерпретацию волн де Бройля, которая сочетает анатомизм (неделимость) и волновые свойства, связанные с тем, что волны де Бройля следует рассматривать, как волны вероятности.

Интенсивность волны де Бройля в какой-либо точке пространства пропорциональна вероятности обнаружить частицу в данной точке.

Статистика микрочастиц не зависит от их количества и одинакова, как для одиночных частиц, так и для их потоков.

Поясним появление интерференции. Перед попаданием в интерферометр все электроны проходят одинаковую разность потенциалов, а значит имеют одну и ту же длину волны λ де Бройля. В какую точку экрана попадает электрон, достоверно предсказать не возможно, но вероятность этого попадания пропорциональна интенсивности волны де Бройля в этой точке, значит электрон, в основном, будет попадать в те точки экрана, для которых выполняется условие максимума.

Из оптики известно:

Рассмотрим движение электрона с постоянной скоростью в отсутствии действия внешних сил, при этом состояние электрона описывается уравнением волны де Бройля.

Такой электрон равновероятно обнаружить в любой точке пространства. Волна де Бройля – простейший частный случай некоторой функции состояния микрочастицы.

В квантовой физике для описания состояния микрочастицы вводится некоторая волновая функция , сложным образом зависящая от и . На опыте, волновая функция не наблюдается и сама по себе физического смысла не имеет, хотя ее называют амплитудой вероятности.

Вероятность обнаружения частицы в объеме в окрестности точки в момент времени :

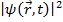– плотность вероятности, вероятность обнаружения частицу в единичном объеме.

Условие нормировки волновой функции:

Равенство единице вероятности обнаружения частицы в объеме 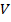означает достоверность данного события.

Рассмотрим вероятность волны де Бройля.

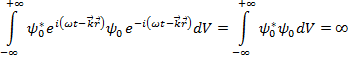
Данный интеграл расходится, в таком случае выполнение условия нормировки требуют на ограниченной области:

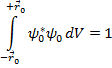
Волновая функция позволяет определить среднее значение физических величин, наблюдаемых в опыте, например среднее значение координаты можно рассчитать следующим образом:

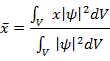
§22. Соотношение неопределенностей Гейзенберга 1927г.

Волновые свойства микрочастиц нельзя понять, если представлять их материальными точками, движущимися по определенным траекториям. Кроме того, характеризовать микрочастицу классическими величинами, такими, как , , … также нельзя, т.к., строго говоря, эти величины микрочастице не свойственны.

Описание микрочастицы в квантовой физике выполняется с помощью волновой функции , степень применимости классических понятий для характеристики микрочастиц определяется соотношениями неопределенности Гейзенберга, которые являются математической формулировкой универсального закона природы, корпускулярно-волнового дуализма.

1)

Неопределенность координаты:

Неопределенность компоненты импульса:

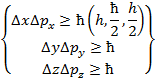
Никаких ограничений на перекрестные произведения нет.

Т.о., если мы абсолютно точно знаем координату, то ее неопределенность стремится к нулю, следовательно мы ничего не знаем про импульс.

Рассмотрим дифракцию электронов на щели.

До прохождения щели мы точно знаем импульс электрона и, соответственно, ничего не знаем про координату. При прохождении щели неопределенность становится порядка размера щели, значит:

Рассмотрим центральный максимум, ограниченный минимумами порядка

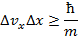
Чем больше масса частицы, тем точнее возможно совместное измерение координаты и скорости.

Классическое определение скорости:

Уравнение траекторий:

В силу соотношений неопределенности, понятие траекторий для микрочастицы теряет смысл.

Рассмотрим пример шарика, наблюдаемого в микроскоп.

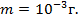
Как видим, ошибка скорости не значительна, в опыте не регистрируется, а значит можно считать, что шарик движется по некоторой траектории.

Рассмотрим пример электрона в атоме.

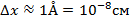
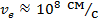
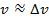
Следовательно, мы ничего не знаем о скорости электрона и не можем говорить о какой-либо траектории или орбите.

Рассмотрим пример движения электронов, ускоренных разностью потенциалов вдоль одной оси со скоростью .

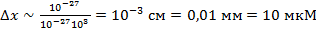
В данном случае можно говорить о траектории электрона.

Оценим с помощью соотношений неопределенности линейные размеры атома водорода и его минимальную энергию.

Если бы электрон упал на ядро, то мы бы точно знали его координату и импульс, но это запрещено соотношениями Гейзенберга.

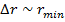
1) 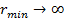- не имеет смысла, т.к. атома, в таком случае, не существует.

2)

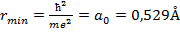
Выводы:

1) Согласно квантовой механике, существует принципиальный предел точности измерений, который лежит в основе природы и не может быть превзойден никакими улучшениями условий эксперимента.

2) Понятие траекторий для пространственного движения микрочастиц теряет смысл.

3) Для микрочастиц теряет смысл разделение энергии на кинетическую и потенциальную.

4) Классический момент импульса в квантовой механике также теряет смысл.

5) Квантовая микрочастица никогда не бывает в состоянии покоя.

(2) Кроме соотношений неопределенности для координаты и импульса, известны соотношения и для всех других сопряженных пар физических величин, в частности, для энергии и времени:

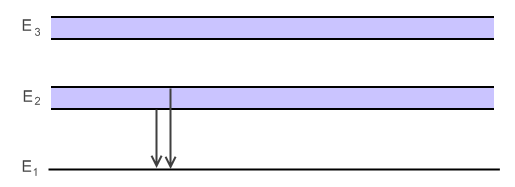
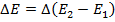
Любой возбуждаемый уровень уширен, а значит уширена и спектральная линия:

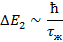
§23. Постулаты квантовой физики.

Уравнение Шредингера 1925г.

1) Движению частицы сопоставляется волновая функция

2) Волновая функция подчиняется уравнению Шредингера

3) Любой физической величине сопоставляется линейный самосопряженный оператор , собственные значения которого вещественны

4) Принцип суперпозиции квантовых состояний

5) Тождественные квантовые частицы принципиально не различимы, для них выполняется принцип Паули

Уравнение Шредингера:

Нестационарное или временное уравнение Шредингера для релятивистской частицы без спина.

- потенциальная функция, если она не зависит явно от времени , то она имеет смысл потенциальной энергии в данной точке пространства.

- оператор кинетической энергии.

- оператор Лапласса

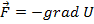
Зная потенциал, всегда можно найти силу.

Будем считать, что потенциал 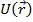зависит только от координаты и решение уравнения будем искать в виде стационарных волновых уравнений:

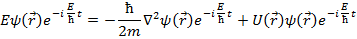
Стационарное уравнение Шредингера (СУШ):

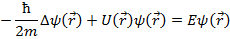
Вероятность обнаружения частицы в объеме окрестности точки в момент времени :

Для стационарных волновых функций вероятность не зависит от времени.

Математические требования к волновой функции:

1) должна быть непрерывна, конечна и однозначна

2) должна быть непрерывна и конечна

3) В области, где потенциальная энергия , частица находится не может, значит волновая функция в этой области 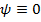, из условия непрерывности следует, что волновая функция и на границе с этой областью.

В квантовой механике всем динамическим переменным сопоставляются линейные операторы, например, в координатном представлении оператором координаты умножается на координату:

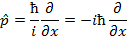
Оператор называют Эрмитовым или сопряженным, если выполняется следующее условие:

Собственные значения таких операторов действительные.

СУШ в операторной форме:

Уравнение на собственные функции и собственные значения Гамильтона:

Решая УШ, получаем набор значений энергии 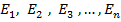, которым соответствуют функции

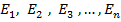- собственные значения или энергитический спектр Гамильтониана.

Т.о. квантование энергии автоматически вытекает из вида УШ без каких-либо дополнительных условий.

Например, правило квантования Бора:

Спектр Гамильтониана может быть дискретным (соответствует финитному движению), либо непрерывным (инфинитному движению), или смешанным.

Вид спектра зависит от вида конкретного оператора . Допустим, найдены все собственные значения энергий и они дискретны, пусть, также, эти значения невырождены (каждому конкретному состоянию соответствует свое, отличное от других, значение энергии):

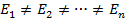
В этом случае, набор волновых функций образует полную или базисную систему функций, и все они ортогональны друг другу.

Условие нормировки:

§24. Принцип суперпозиции квантовых состояний.

Постулируется в следствии наличия волновых свойств микрочастиц.

Классический принцип суперпозиции: действие суммарного поля равно действию отдельных полей.

В квантовой механике исходят из УШ. Если при этом найдены все собственные функции оператора , то в силу линейности операторов, решение УШ может быть представлено, как суперпозиция:

При всяком измерении энергии получается только какое-либо одно из энергитического спектра 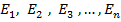, при этом вероятность данного результата измерений равна соответствующему

– коэффициенты разложения волновых функций по полному состоянию или по базису волновых функций.

Пример.

Результат этого эксперимента объясняется принципом суперпозиции.

§25. Примеры движения квантовой частицы в стационарных

силовых полях.

СУШ:

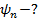
1) 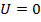- случай движения квантовой частицы в отсутствии действия внешних сил

2) Частица в бесконечно глубокой потенциальной яме ширины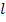

3) Квантовый гармонический осциллятор

Пример потенциального барьера. Физика туннельных диодов. Эффект Джозефсона.

§26. Момент импульса квантовой теории.

Согласно классической физике:

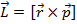
- в силу соотношения Гейзенберга, данное определение уже не применимо не смотря на то, что момент импульса является очень важной величиной в атомной физике.

Рассмотрим атом водорода по Бору:

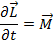
Т.к. для центрального поля момент силы равен нулю, значит сохраняется закон сохранения момента импульса.

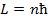
В квантовой механике для описания орбитального механического момента импульса вводится четыре оператора: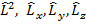

В силу соотношения неопределенности, из данных четырех операторов одновременно абсолютно точно могут быть определены только два: 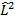и одна из проекций (чаще выбирают )

Модель можно представить в виде прецессии вдоль выбранной оси.

Т.к. пространство изотропно, т.е. не зависит от направления. То в качестве оси Oz можно выбрать любую, и направление прецессии момента импульса в данном случае не определено.

Решение этих уравнений дает следующий спектр:

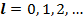– орбитальное квантовое число.

В квантовой физике орбитальный механический момент 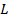квантуется, т.е. принимает не любые значения, а строго определенные, дискретные, зависящие от орбитального квантового числа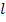

- главное квантовое число.

Спектр проекции орбитального механического момента тоже квантуется:

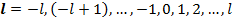- магнитное орбитальное квантовое число.

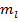- принимает 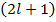значений.

В квантовой физике проекция меньше собственного значения:

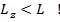
Состояние электрона:

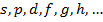
Состояние атома:

Рассмотрим пример.

Пусть электрон в атоме находится в 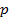состоянии, т.е. орбитальное квантовое число . В классической физике проекция момента импульса на выбранную ось может принимать непрерывные значения:

В квантовой физике проекция 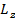квантуется:

Правило сложения орбитального момента: если система состоит из электронов, каждый из которых характеризуется собственным орбитальным квантовым числом 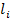, то суммарный орбитальный момент системы есть также квантово-механический вектор, собственное значение которого вычисляется следующим образом:

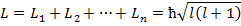
(от минимального по модулю через 1 до максимального по модулю)

Рассмотрим пример.

Пусть первый электрон в состоянии 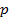, второй электрон в состоянии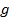

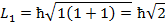
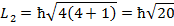
Можно представить атом, как рамку с током, а значит с любым механическим моментом движения всегда связан магнитный момент:

Отношение магнитного момента движения к орбитальному называют гиромагнитным или магнитомеханическим отношением.

Магнитон Бора – единственная единица измерения магнитных моментов:

Проекция магнитного орбитального значения квантуется.

§27. Гипотеза Уленбека (Юленбека) и Гаудсмита о спине электрона.

Опыты Штерна и Герлаха.

Предпосылкой гипотезы о спине являлись следующие факты:

1) Наблюдения Штерна и Герлаха

2) Магнитомеханические опыты Энштейна, де Гааза, Барнетта, в которых было установлено в два раза большее значение гиромагнитного отношения.

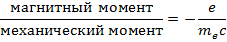
3) Дублетная структура термов щелочных металлов.

Уленбек и Гаудсмит предположили, что у электрона есть не только орбитальный механический момент 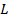и соответствующий ему магнитный орбитальный момент 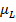, но и собственный (внутренний) механический момент 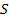, называемый спином, и соответствующий ему спиновый магнитный момент .

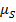Дата добавления: 2014-11-20