Тема: Аксонометрические проекции

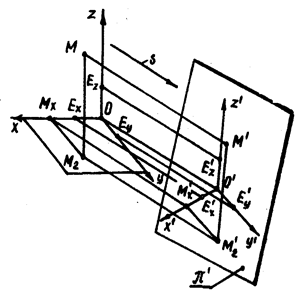
Рисунок 11

Возьмем точку М и прямоугольную декартовую систему координат Oxyz (рис.11). |OE_X|=|OE_Y|=|OE_Z| - натуральный масштаб. Основание перпендикуляра, опущенного из точки М на координатную плоскость Oxy, определяет прямоугольную проекцию М₂ точки

Рис 2.1

М. Прямая проведенная через точку М₂ перпендикулярно к Ox, пересекает ее в точке М_x. Тогда: x=|ОМ_x| ¤ |ОЕ_x| - абсцисса; y =|M_xM₂| ¤ |OE_y| - ордината; z=|M₂M| ¤ |OE_z| - аппликата; OM_xM₂M

–натуральная координатная ломаная точки M. Точку М вместе с натуральной системой координат Oxyz спроецируем в направлении s на аксонометрическую плоскость проекций p¢. Параллельную проекцию O¢x¢y¢z¢ натуральной системы координат Oxyz называют аксонометрической системой равны между собой); O¢M¢_xM¢₂M¢ - аксонометрическая координатная ломаная; М¢ - аксонометрическая и М¢₂ – вторичная проекция точки М.

На основании свойства 4 имеем, что (M¢_xM¢₂)|| (О¢Е¢_y) и (M¢₂M¢)|| (О¢Е¢_z). Аксонометрические координаты: x¢=|О¢М¢_x| ¤ |О¢Е¢_x|; y¢ =|M¢_xM¢₂| ¤ |O¢E¢_y|; z¢=|M¢₂M¢| ¤ |O¢E¢_z|. На основании свойства 5 можно утверждать, что натуральные и аксонометрические координаты точки (численно) равны между собой x= x¢, y= y¢, z= z¢.

Чертеж, состоящий из аксонометрической М¢ и вторичной М¢₂ проекции точки, является обратимым. Чтобы доказать это, покажем построение точки М. Пусть имеются натуральная Oxyz и аксонометрическая O¢x¢y¢z¢ системы координат, аксонометрическая М¢ и вторичная М¢₂ проекции точки М. Через точку М¢₂ проводим прямую, параллельную оси O¢y¢, до пересечения с осью O¢x¢ в точке M¢_x. Через точку M¢_x проводим прямую, параллельную направлению проецирования s, до пересечения с осью Ox в точке M_x. Прямые, проведенные через точку M_x параллельно Oy и через точку М¢₂ параллельно s, пересекаются в точке М₂. Наконец, прямые, проведенные через точку М₂ параллельно Oz и через точку М¢ параллельно s, пересекаются в точке М.

Основная теорема аксонометрии.

В 1853 году К.Польке (1810-1896) доказал основную теорему параллельной аксонометрии: три отрезка О¢Е¢_x , О¢Е¢_y, О ¢Е¢_z произвольной длины, лежащие в одной плоскости и выходящие из точки О¢ под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков ОЕ_x, ОЕ_y, и ОЕ_z, отложенных на прямоугольных осях координат от начала О. На основании этой теоремы можно совершенно произвольно выбрать систему аксонометрических осей и масштабов.

Рассмотрим построение аксонометрической проекции (сокращенно: аксонометрии) точки А(4,2,5), заданной координатами: x=4, y=2, z=5. На основании теоремы Польке проводим три луча O¢x¢, O¢y¢, O¢z¢, которые образуют между собой произвольные углы, и отложим, начиная от точки O¢ три произвольных отрезка – аксонометрические масштабы О¢Е¢_x , О¢Е¢_y, О ¢Е¢_z (рис. 12). На ось O¢x¢ отложим четыре отрезка, равные | О¢Е¢_x |. Через полученную точку А¢_x проводим прямую параллельно оси O¢y¢ и отложим на эту прямую 2 отрезка, равные | О¢Е¢_y |. Через полученную вторичную проекцию А¢₂ проводим прямую параллельно оси O¢z¢ и отложив 5 отрезков, равных |О ¢Е¢_z |, получим искомую аксонометрию А¢ точки А.

Рис.2.2

Если заданы аксонометрия А¢ и вторичная проекция А¢₂, то можно определить координаты точки А. Для этого через точку А¢₂ проводим прямую, параллельную оси O¢y¢, до пересечения с осью O¢x¢ в точке А¢_x. Отрезок О¢А¢_x делим на отрезок О¢Е¢_x, тогда получим абсциссу точки А. Аналогично y =|А¢_xА¢₂| ¤ |O¢E¢_y| и z=|А¢₂А¢| ¤ |O¢E¢_z|.

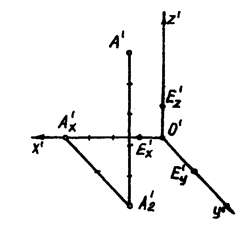
Рисунок 12

Прямая определяется двумя точками, принадлежащими ей. В аксонометрии прямая задается аксонометрической и вторичной проекциями, интересующей нас части (отрезка этой прямой). Если прямая принадлежит координатной плоскости Oxy, то аксонометрическая и вторичная проекции совпадают. Если прямая принадлежит координатной плоскости Oxz, то ее вторичная проекция совпадает с осью O¢x¢.

Пример 1. Требуется построить аксонометрическую проекцию сечения пирамиды SABCD плоскостью, определяемой

точкой 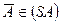и прямой h Ì пл. Oxy (рис. 13).

Решение. Если плоское сечение пирамиды спроецировать из вершины S на плоскость основания, то между плоскостями сечения и основания устанавливается коллинеация, которая изображается на плоскость аксонометрических проекций в гомологию. Гомология определена центром S¢, осью h¢ и парой соответственных точек 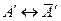. Определяем точку 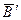, соответствующую точке В¢ (см. рис.14). Продолжим отрезок А¢В¢ до пересечения с осью гомологии h¢ в точке . Прямая, соединяющая две точк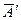и и , пересекается с ребром 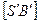в точке 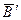. Аналогично, строятся точк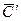и и 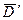. Четырехугольник 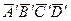является аксонометрической проекцией искомого сечения.

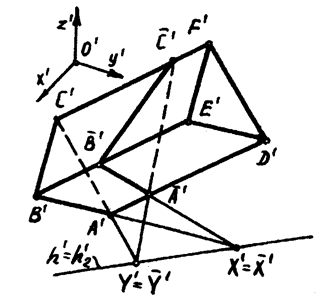
Пример 2. Требуется построить аксонометрическую проекцию сечения треугольной призмы плоскостью, определяемой точкой 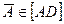и прямой h Ì пл. Oxy (рис3.4).

Рисунок 13	Рисунок 14

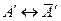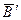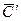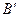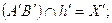
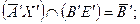
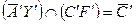Решение. Если плоское сечение призмы спроецировать на плоскость основания в направлении боковых ребер, то между плоскостями сечения и основания устанавливается родство. Родство определено осью h¢ и парой родственных точек . Задача сводится к построению точек и , родственных, соответственно, точкам и . . Треугольник 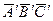является аксонометрической проекцией сечения призмы.

Коэффициенты искажений. Виды аксонометрических проекций. Основная формула аксонометрии

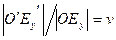Отношение аксонометрического масштаба к натуральному масштабу называется коэффициентом искажения. Различают коэффициенты искажений: - по оси Ох; - по оси Оу; 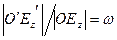- по оси Оz.

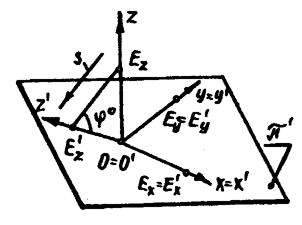
Рисунок 15

По направлению проецирования аксонометрия делится на прямоугольную 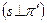и косоугольную .

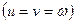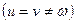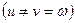По соотношению между коэффициентами искажений аксонометрия делится на изометрию , диметрию , или , или 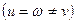и триметрию .

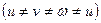Не теряя общности, можно считать,

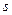что плоскость аксонометрических проекций совпадает с координатной плоскостью (рис. 11). Спроецируем натуральную систему координат в направлении на плоскость . При этом 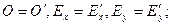поэтому 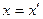и 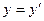. Тогда точка 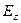проецируется в точку 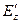. - прямоугольный треугольник и 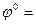(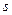,^Ù ) – угол между направлением проецирования и плоскостью проекций. Вычислим сумму квадратов коэффициентов искажений:

; ; .

.

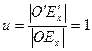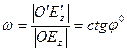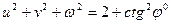Для прямоугольной аксонометрии .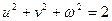

Прямоугольная проекция плоского угла.

Теорема о прямоугольной проекции прямого угла

Пусть сторона 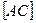треугольника АВС лежит в плоскости (рис. 16). 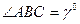. Сторона (АВ) наклонена к плоскости под углом 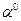, а сторона (ВС) – под углом 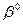. Точка 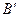- прямоугольная проекция вершины В, а точки А¢ и С¢ совпадают с соответствующими точками А и С. 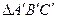- прямоугольная проекция треугольника АВС, угол 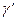- прямоугольная проекция угла .

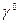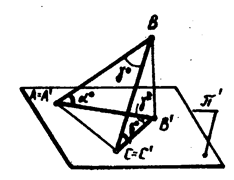
Рисунок 16

Известно, что 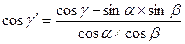. Пусть задан прямой угол (т.е. 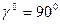), который проецируется в прямой угол (т.е. ). Тогда из вышеприведенной формулы получим следующее равенство 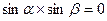, которое имеет место только тогда, когда 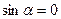или 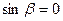. Это значит, что хотя бы одна сторона рассматриваемого угла должна располагаться параллельно плоскости проекции. Отсюда теорема:

Для того чтобы прямой угол проецировался прямоугольно в виде прямого угла, необходимо и достаточно, чтобы, по крайней мере, одна его сторона была параллельна плоскости проекций, а другая сторона – не перпендикулярна к последней.

Основная литература: 1.7.1 (24…34,57….60),1.7.1 (17…23),

Дополнительная литература:

1.7.17 (24…35, 41…44), 1.7.10.(25…30, 46…50), 1.7.11. (_15….44), 1.7.17 (300…315), 1.7.10 (203…212), 1.7.11 (234…258).

Дата добавления: 2014-11-20