Умова, при якій дві прямі лежать в одній площині

Відстань від точки до площини і від точки до прямої на площині

Відстань від точки до площини. Нехай в системі координат задані площина і точка (рис. 8.10).

Відстань 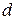від точки 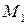до цієї площини рівна модулю проекції вектора 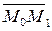на напрямок нормального вектора , де довільна точка площини. Отже,

.

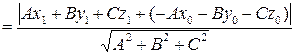Так як точка належить даній площині, то , тобто . Отримаємо:

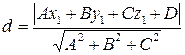. (8.23)

Приклад 8.9. Знайти відстань від точки 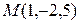до площини .

Розв’язок. За формулою (8.23)

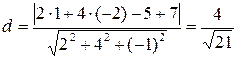t

Відстань від точки до прямої на площині. Нехай в системі координат задана пряма 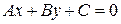і точка .

Відстань від точки 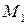до цієї прямої знаходиться за формулою

. (8.24)

Вивід формули (8.24) аналогічний до виводу формули (8.23).

Нехай прям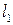і і задані рівняннями

, .

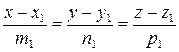Їх напрямні вектори відповідно і (рис.8.11).

Точка лежить на прямій 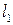, а точка 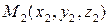– на прямій . Умовою, при якій дві прямі належать одній площині, є компланарність векторів 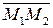, , 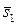, тобто (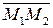, , 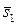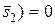або

. (8.25)

При виконанні умови (8.25) прям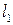і і перетинаються, якщо вектори 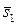, неколінеарні, і , якщо .

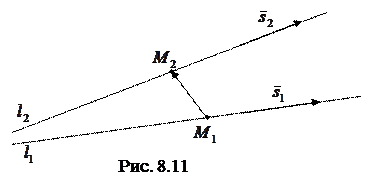
Приклад 8.10. Вияснити, чи перетинаються прямі

,

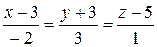
і, якщо перетинаються, знайти їх точку перетину.

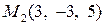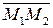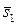Розв’язок. Точка лежить на першій прямій, а точка – на другій. Напрямні вектори даних прямих відповідно і . Умовою, при якій прямі перетинаються, є компланарність векторів , , . Знайдемо мішаний добуток даних векторів

.

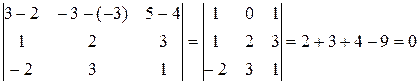Отже, умова (8.25) виконується, тобто прямі перетинаються.

Знайдемо точку перетину прямих, розв’язавши систему їх рівнянь:

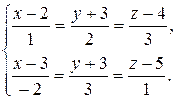
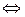
Таким чином, точка перетину даних прямих має координати . t

Теоретичні питання

8.1. Записати рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора.

8.2. Записати загальне рівняння площини.

8.3. Записати рівняння прямої на площині, що проходить через задану точку перпендикулярно до заданого вектора.

8.4. Записати загальне рівняння прямої.

8.5. Записати канонічні рівняння прямої.

8.6. Записати параметричні рівняння прямої.

8.7. Записати рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом.

8.8. Записати рівняння прямої з заданим кутовим коефіцієнтом.

8.9. Записати загальні рівняннями прямої в просторі.

8.10. Записати рівняння прямої, що проходить через дві точки.

8.11. Записати рівняння прямої у відрізках.

8.12. Записати рівнянням площини, що проходить через три точки.

8.13. Записати рівняння площини у відрізках.

8.14. Як визначається кут між площинами?

8.15. Які умови паралельності та перпендикулярності двох площин?

8.16. Як визначається кут між прямими, заданими: а) загальними рівняннями; б) канонічними рівняннями; в) рівняннями з заданим кутовим коефіцієнтом?

8.17. Які умови паралельності та перпендикулярності двох прямих, заданих: а) загальними рівняннями; б) канонічними рівняннями; в) рівняннями з заданим кутовим коефіцієнтом?

8.18. Як визначається кут між прямою і площиною?

8.19. Які умови паралельності та перпендикулярності прямої і площини?

8.20. Чому рівна відстань від точки до площини і від точки до прямої на площині?

8.21. Записати умову перетину двох прямих у просторі.

Задачі та вправи

Дата добавления: 2014-11-29