Скалярное произведение векторов. Свойства скалярного произведения

Проекция вектора на ось. Свойства проекций

Определение 1.11. Проекцией вектора 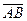на ось 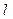называется длина отрезка этой оси, заключённого между проекциями точек A и B, взятая со знаком «+», если направление отрезка совпадает с направлением оси 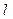, и со знаком «-» в противоположном случае.

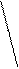
B A

A

B

l l

В ₁ А ₁

А ₁ + В ₁ -

Проекцию вектора 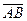на ось l обозначают следующим образом: .

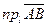Проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью l и вектором, т.е:

,

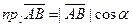где под углом между осью и вектором понимается наименьший угол, на который нужно повернуть ось до совпадения с направлением вектора (рис. 1.4).

B

ö a

A

А ₁ В ₁ l

Рис. 1.4

Отсюда, в частности следует, что равные векторы имеют равные проекции на одну и ту же ось.

Определение 1.12. Скалярным произведением двух векторов 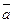и 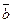называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.∙ 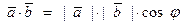, где j — угол между векторам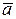и и .

Заметив, что | 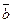| cosj — есть проекция вектора 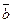на вектор 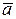, имеем . Аналогично, .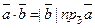

Рассмотрим основные свойства скалярного произведения:

1) Скалярное произведение обладает переместительным свойством:

.

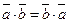2) Скалярное произведение векторов обладает распределительным свойством:

.

3) Чтобы умножить скалярное произведение на число достаточно умножить на это число один из сомножителей

.

4) 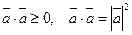. Отсюда .

5) Скалярное произведение векторов равно нулю тогда и только тогда, когда по крайней мере один из векторов-сомножителей является нулевым вектором, или если данные векторы перпендикулярны.

1.1.6. Разложение вектора по ортам в пространстве R³. Понятие вектора в координатной форме

Рассмотрим декартову прямоугольную систему координат OXYZ в пространстве 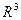, и произвольный вектор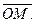

z

М₃

М

О М₂ y

М₁

x Р

Рис. 1.5

Из точки M конца вектора 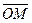проведём прямую, параллельную оси OZ до пересечения в точке P с плоскостью OXY (рис. 1.5). Обозначим через M₁ и M₂ — соответственно, проекции точки P на оси OX и OY. Пусть M₃ — проекция точки M на ось OZ. Тогда будем иметь:

.

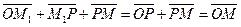Заменив векторы 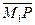и 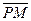равными им векторам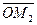и и 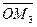, получим

. (1.1)

Равенство (1.1) показывает, что всякий вектор в R³ можно представить в виде суммы трёх векторов, лежащих на осях координат. От точки O в направлении каждой оси отложим по вектору длины, равной 1. Обозначим эти вектора через 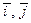и , соответственно и назовём их ортами. Обозначим через x, y и z — проекции вектора 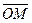на координатные оси OX, OY и OZ, соответственно. Так как векторы 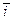и лежат на одной оси OX, то = 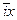. Аналогично, = 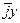, 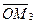= . Следовательно, равенство (1.1) может быть переписано в виде

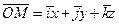. (1.2)

Равенство (1.2) называют разложением вектора 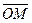по ортам 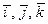. Вместо полной записи (1.2) часто пользуются сокращенной 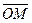={ x, y, z }, где x, y, z — проекции вектора 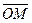на координатные оси, которые будем называть координатами вектора 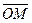. Соответственно орты имеют координаты: , , .

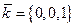На плоскости разложение вектора 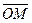по ортам имеет вид 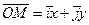(рис. 1.6).

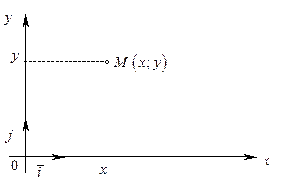
Рис. 1.6

Дата добавления: 2014-12-08