Теоретическая часть. Проанализируйте поведение системы при различных параметрах α, β, ε, δ, а также при различных х0 и у0

ТЕМА 3. ИНФОРМАЦИЯ И ЖИВОЙ ОРГАНИЗМ. ТЕОРИЯ ИНФОРМАЦИИ.

Выполнение работы

Проанализируйте поведение системы при различных параметрах α, β, ε, δ, а также при различных х₀ и у₀. Для этого:

1) Построить серию графиков зависимостей x(t) и y(t) (на одном рисунке) и соответствующие им фазовые портреты системы.

2) Оцените из графиков период колебаний численностей хищников и жертв.

3) Оцените из графиков, при каких отклонениях от x_ст и у_ст гармонические колебания сменяются сложными колебаниями, а форма фазовой траектории становится отличной от элисоидальной.

4) Подумайте при каких соотношениях параметров модель «хищник-жертва» превращается в модель естественного роста.

5) Сравните расчетные кривые изменения x(t) и y(t) с экспериментальными кривыми, представленными на рис.2.4.

Параметры	ε, 1/год	β, 1/год	α	δ	xст	уст	Начальные условия
x0=xст+Δx	y0=yст+Δy
1система	0.5	0.72	0.01	0.009			x0=xст+0.05xст	y0=yст
2система	0.5	0.72	0.01	0.009			x0=xст+0.25xст	y0=yст
3система	0.5	0.72	0.01	0.009			x0=xст+ 0.5xст	y0=yст
4система	0.5	0.72	0.01	0.009			x0=xст+ xст	y0=yст
Предел xст+ 0.75xст

Литература:

1.Антонов В.Ф. и др. Биофизика. – М.: Владос, 2006. – С.163-180.

2. Владимиров Ю.А., Рощупкин Д.И., Потапенко А.Я., Деев А.И. Биофизика: учебник. – М.: Медицина, 1983. – С.88-94.

3. Волькенштейн М.В. Биофизика. – М.: Наука, 2009.

4. Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическое моделирование в биофизике. Введение в теоретическую биофизику. – М.: ИКН, 2004. – 472 с.

Контрольные вопросы.

1. Что такое модель? В чем сущность процесса моделирования? Какие преимущества имеет этот метод?

2. Какие типы моделей Вы знаете?

3. Назовите основные этапы моделирования?

4. Что такое допущения в моделях?

5. Понятие об адекватности моделей?

6.Основные положения модели Мальтуса.

7. Основные положения модели Ферхюльста.

8. Основные положения модели Вольтера-Лотки.

Информация (от лат. informatio - разъяснение, осведомление) - это один из широко используемых на сегодня терминов, которые употребляет человек в процессе деятельности. Создаются информационные центры, передаются информационные программы, говорят о лавинном росте информационных потоков, сообщается информация «для размышления» и т.д. Практически одновременно и взаимосвязано с появлением кибернетики в XX столетии создается теория информации - раздел кибернетики, посвященный математическому описанию процессов получения, хранения, переработки и передачи информации.

Эта теория возникла в ходе решения задач передачи потоков сообщений по каналам связи в технических системах, и первый фундаментальный труд принадлежит К. Шеннону «Математическая теория связи» (1948 г.). Сегодня понятие «информация» является одной из основных философских категорий, наряду с такими категориями, как материя, энергия, без которых невозможно описание функционирования живых систем.

К основным понятиям теории информации относятся: сообщение, сигнал, количество информации, энтропия, кодирование, пропускная способность канала связи.

Сообщение - это некоторая информация о событиях, закодированная в форме определенного сигнала.

Сигнал - физический носитель информации. Сигналом может быть звук, свет, буква, механический удар и др.

Прежде чем рассмотреть вопрос о количестве информации, необходимо отметить следующие ее свойства:

1. Информация имеет смысл только при наличии ее приемника (потребителя). Если принимающий объект отсутствует, то нельзя говорить о существовании информации. Так, если в комнате работает телевизор, но в ней нет человека, то все, что по­казывается и говорится, не является информацией.

2. Наличие сигнала не обязательно говорит о том, что передается некоторая информация. Информативно только такое сообщение, которое несет в себе что-то неизвестное ранее, в чем нуждается объект, которому оно передается.

3. Информация может передаваться не обязательно только через наше сознание. Она передается и на подсознательном уровне, и на уровне внутренних процессов в организме. Для мышц двигательного аппарата пришедшие к нему нервные импульсы несут информацию о необходимых действиях; для сердца объем крови в диастолу несет информацию о необходимой силе последующего сокращения, перестройка конформации фермента несет информацию для процессов переноса ионов и др.

4. Если событие достоверное (то есть его вероятность р=1), то сообщение о том, что оно произошло, не несет никакой информации для потребителя. Так, если вы в настоящий момент читаете эту страницу и вам кто-то об этом сообщает, то в этом сообщении для вас нет ничего нового, то есть не содержится абсолютно никакой информации.

5. Сообщение о событии, вероятность которого р<1, содержит в себе информацию, и тем большую, чем меньше вероятность события, которое произошло.

Таким образом, чем меньше вероятность некоторого события, тем большее количество информации содержит сообщение о том, что оно произошло.

Так например, если во Вселенной появилась сверхновая звезда, событие крайне маловероятное, об этом сообщают все мировые информационные агентства и газеты, так как в этом сообщении содержится огромное количество информации.

Шеннон дал следующее определение информации:

"Информация, содержащаяся в сообщении, есть мера того количества неопределенности, которое ликвидируется после получения данного сообщения».

Количество информации I (х_i)_, содержащееся в сообщении х_i, равно логарифму величины, обратной вероятности Р(х_i) этого события:

За единицу информации принято количество информации, содержащееся в сообщении о том, что произошло одно из двух равновероятных событий, то есть если Р(А) = Р(В) = 0,5, то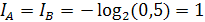

Это количество информации называют бит.

Пример: Сколько бит информации содержит произвольное трехзначное число?

Первая цифра имеет 9 различных значений от 1 до 9 (т.к. 0 в начале числа незначим), вторая и третья - по 10 значений (от 0 до 9). Тогда

бит.

В теории информации источник информации задается в виде множества сообщений X₁, Х₂,...,Х_n, с вероятностями соответственно Р₁, Р₂,...,Р_n. В этом случае среднее количество информации, приходящееся на одно сообщение, определяется по формуле Шеннона: , где i = 1, 2,... n.

Пример: Рассчитаем количество информации I_А и I_B в сообщениях о событиях А и В, вероятности которых: Р (А) = 3/4 и Р(В) = 1/4.

Для сообщения A: I_A =-log ₂ (3/4) = 0,42 бит.

Для сообщения В: I_B = -log ₂ (l/4) = 2,0 бит.

Среднее количество информации на одно сообщение:

бит

Величина I рассматривается как мера неопределенности сведений об источнике информации, которая имела место до приема сообщений и была устранена после их получения.

Эту меру неопределенности называют энтропией (Н) источника информации, приходящейся на одно сообщение. Таким образом:

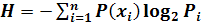
Среднее количество информации и энтропия Н численно равны, но имеют противоположный смысл.

Чем из большего числа сообщений получатель информации должен сделать выбор, тем большее значение имеет информационная энтропия.

Для источника с единственно возможным сообщением, вероятность которого стремится в 1 (Р→1), энтропия стремится к нулю (Н →0).

Если все к возможных сообщений источника равновероятны (Р(х_i) = 1/к), то его энтропия Н максимальна: .

Предполагается, что каждому сообщению соответствует только одно из возможных состояний источника. В этом случае величина Н может служить мерой неорганизованности системы, являющейся источником информации. Чем менее организована система, тем больше число ее возможных состояний и величина максимальной энтропии;

Для примера рассмотрим три источника информации А, В и С, характеризуемые тремя сообщениями каждый: I, II и III с вероятностями, указанными ниже:

Сообщения	I	II	III
А	0,8	0,1	0,1
В	0,4	0,4	0,2
С	0,33	0,33	0,33

Вычислим энтропии источников А, В и С на одно сообщение:

Как видим, источник информации С, который характеризуется сообщениями с одинаковыми вероятностями (Р=0,33), имеет самую большую Н = Н_mах, то есть самую большую степень неопределенности.

Уровень определенности (детерминированности) источника информации характеризуется величиной R=1-(H/H_max), где Н - энтропия на одно состояние источника информации, Н_mах - максимальная энтропия на одно сообщение, когда все сообщения равновероятны. В нашем примере R_C=0, R_B = 0,02, R_A = 0,4.

Если R=1,0-0,3, источник информации считается детерминированным, R=0,3-0,1 - вероятностно детерминированным, R<0,1 вероятностным (стохастическим). Таким образом, источники В и С - стохастические, а источник А - детерминированный.

Среднее количество информации, которое может получить объект, зависит от характеристик канала связи. Каналом связи может быть провод, световой луч, волновод, нервные волокна, кровеносные сосуды и др. Основной характеристикой канала связи является его пропускная способность. Она будет определяться предельной скоростью передачи информации, измеряемой в бит/с.

Для передачи сообщения по каналу информация кодируется, например, положение флага на флоте, азбука Морзе, последовательность, частота, длительность импульсов в нервной сети и др. На приемной стороне необходим декодер, который осуществляет обратное кодеру преобразование: код сигнала преобразуется в содержание сообщения. Блок-схема канала связи показана на рис. 3.1.

Рис. 3.1. Блок-схема канала связи

При передаче информации по каналу связи могут происходить ее искажения за счет помех из внешней среды и нарушений в самой линии.

Эффективными способами борьбы с искажениями информации является создание ее избыточности и передача сигналов по большому числу параллельных каналов. Оба эти способа широко используются в организме человека. В нервных сетях всегда обеспечивается дублирование основного сообщения большим числом параллельных сигналов, поэтому количество рецепторов значительно превышает количество нейронов, к которым от них поступают сигналы.

Пропускная способность любых рецепторных аппаратов существенно выше возможностей осознания сенсорной информации. Человеческое сознание пользуется очень малой долей информации, поставляемой в мозг периферическими отделами анализаторов - сенсорными входами. Так, например, максимальный поток информации в процессе зрительного восприятия, осознаваемого человеком, составляет всего 40 бит/с, тогда как информационная емкость потока нервных импульсов в зрительных нервах оценивается величиной 10⁷ бит/с. За счет столь огромной избыточности достигается высокая надежность процессов в организме.

Дата добавления: 2014-11-29