Предельные теоремы

Для математической статистики принципиальное значение имеют две предельные теоремы.

Закон больших чисел. Пусть имеется последовательность одинаково распределенных независимых случайных величин y₁, y₂, y₃,…, имеющих конечное математическое ожидание М.Тогда, каковы бы ни были ε > 0 и η > 0, найдется столь большое п, что

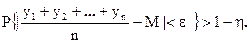
Иными словами, если число слагаемых очень велико, то их среднее арифметическое, с вероятностью сколь угодно близкой к единице, оказывается близким к их математическому ожиданию.

Более сильное утверждение: среднее арифметическое, о котором шла речь, становится близким к М не только для одного значения п, но и для всех последующих.

.

Для иллюстрации значения только что сформулированной теоремы приведем следующий постоянно используемый пример. Предположим, что в одних и тех же условиях производятся измерения некоторой величины Хбез систематической ошибки. Случайные ошибки, совершаемые в отдельных измерениях, независимы и, в силу неизменности условий, одинаково распределены. На основании закона больших чисел среднее; арифметическое результатов измерений с подавляющей вероятностью будет как угодно близко к измеряемой величине Х.. Это правило широко используется в экспериментальных науках.

Центральная предельная теорема. Если независимые случайные величины одинаково распределены и имеют конечную дисперсию D, то, согласно центральной предельной теореме, при их числе зависимая переменная должна иметь нормальное распределение.

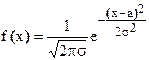
Теорема находит весьма широкое применение на практике. При решении ряда вопросов приходится сталкиваться с такой ситуацией, когда исследуемая (зависимая) случайная величина является суммой большого числа независимых слагаемых, влияние каждого из которых на сумму очень мало. Так, на отклонение снаряда от цели влияют незначительные ошибки наведения и прицеливания, малые колебания плотности атмосферы и направления ветра, неточности в обточке стакана и головки снаряда, незначительные неточности в количестве взрывчатых веществ и т. д. Все эти причины малы в отдельности, но в совокупности приводят к заметному результату — рассеиванию снарядов при стрельбе. На основании центральной предельной теоремы можно до наблюдения того или иного явления утверждать, что отклонение снаряда от цели имеет нормальное распределение или близкое к нему.

Дата добавления: 2014-12-16