
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для выполнения лабораторной работы 11 2 страница
|
|
|
|
Коэффициенты Стьюдента Таблица 4.
| Число измерений n | Доверительная вероятность p | |||||
| 0.8 | 0.9 | 0.95 | 0.98 | 0.99 | 0.995 | |
| 3.077 | 6.313 | 12.706 | 31.820 | 63.656 | 127.656 | |
| 1.885 | 2.920 | 4.302 | 6.964 | 9.924 | 14.089 | |
| 1.638 | 2.353 | 3.182 | 4.540 | 5.840 | 7.458 | |
| 1.533 | 2.132 | 2.776 | 3.746 | 4.604 | 5.597 | |
| 1.476 | 2.015 | 2.570 | 3.649 | 4.032 | 5.893 | |
| 1.439 | 1.943 | 2.446 | 3.142 | 3.707 | 4.316 | |
| 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.229 | |
| 1.397 | 1.860 | 2.306 | 2.897 | 3.832 | 4.501 | |
| 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 4.297 | |
| 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | |
| 1.363 | 1.795 | 2.201 | 2.718 | 3.105 | 3.496 |
В ячейках таблицы 4 находятся коэффициенты tnp. В нашем примере с числом измерений n=6, нас будет интересовать только строка для шести измерений. В ней можно выбрать любой из коэффициентов Стьюдента, но от этого выбора будет зависеть доверительная вероятность p нашего результата определения длины волны света. Если величина p будет небольшой, то и надежность полученного результата окажется невелика, что неприемлемо.
Например, если взять коэффициент tnp =1.476 из колонки с p=0.8, то это будет означать, что доверять нашему результату измерений можно только на 80%, а в остальных 20% веры нашему результату не будет (кто, например, пойдёт к врачу, зная, что каждого пятого больного он лечит неправильно?!). Можно, в погоне за хорошей надёжностью, взять коэффициент tnp =5,893 из последней колонки таблицы (p=0,995). Здесь надежность составляет 99,5% - это очень хороший результат, но и коэффициент tnp весьма велик, т.е. итоговая случайная погрешность 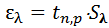 будет очень велика. Надёжный, но грубый результат, тоже никому не нужен.
будет очень велика. Надёжный, но грубый результат, тоже никому не нужен.
Требуется найти разумный компромисс между не очень маленькой вероятностью Р и не очень большим коэффициентом tnp. Примером такого компромисса для шести измерений можно считать tnp = 2,57 для вероятности Р=0,95. Этот коэффициент Стьюдента можно применить в формуле (14) для расчета случайной погрешности измерения длины волны света.
4. Определение систематической погрешности ϴλ длины волны света.
Детальный (достаточно длинный) вывод формулы для расчета систематической погрешности ϴλ можно посмотреть в приложении (Б). Здесь же воспользуемся конечным результатом этого вывода, формула (15):
ϴλ = 0,0325×λср,(15)
где λср- средняя длина волны света по результатам шести измерений (в нашем примере измерений шесть, возможно у вас будет иное их число в соответствии с указаниями преподавателя из-за другой применяемой дифракционной решетки).
5.Расчет суммарной погрешности измерений Δ λ длины волны света.
Следующая формула (16) позволяет найти полную (суммарную) погрешность измерений с учётом как случайной, так и систематической погрешностей:
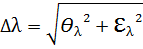 (16)
(16)
6.Запись окончательного результата.
Окончательный результат принято записывать в следующем виде:
 (нм) при p=0,95, (17)
(нм) при p=0,95, (17)
где вместо многоточий должны быть ваши числовые данные.
Результат для длины волны будет в нанометрах, как в этом примере, но можно перевести эти числовые данные и в метры (1нм=10 -9 м).
7. Вывод.
В выводе можно указать, насколько велика или мала оказалась итоговая погрешность эксперимента, насколько надежен оказался полученный результат. Кроме того, можно сопоставить полученное значение длины волны красного света с известными литературными данными и отметить или их совпадение (т.е. попадание литературных данных в доверительный интервал результатов измерений  ), или несовпадение (и возможные причины оказавшегося несовпадения).
), или несовпадение (и возможные причины оказавшегося несовпадения).
Форма отчета по данной лабораторной работе приведена в приложении (А).
5.КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое дифракция?
2. Что такое интерференция?
3. Как записывается формула для дифракционной решетки?
4. Что такое дифракционная решетка?
5. Как, с помощью дифракционной решетки, определить длину волны света?
6. Сколько дифракционных максимумов можно наблюдать на экране?
7. О чём говорит принцип Гюйгенса?
8. Что такое «нулевой максимум»?
9. Как скажется на дифракционной картине (на экране) уменьшение параметра дифракционной решетки?
10. При каком условии дифракция становится заметной (большой)?
6.СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Ивлиев А.Д. Физика: Учебное пособие для вузов. СПб: Лань, 2008. 671 с.
Ивлиев А.Д. Физика. Квантовая механика. Физика атомов и молекул. Физика твердого тела. Физика атомного ядра и элементарных частиц: учеб. пособие для вузов. Екатеринбург: Издательство УГТУ-УПИ, 2005. 247 с.
Ивлиев А.Д. Классическая механика. Специальная теория относительности. Электричество и магнетизм. Колебания и волны. Молекулярная физика и термодинамика: учеб. пособие для вузов. Екатеринбург: Издательство УГТУ-УПИ, 2004. 617 с.
Ивлиев А.Д. Физика: Классическая механика. Специальная теория относительности. Электричество и магнетизм. Колебания и волны. Молекулярная физика и термодинамика: учеб. пособие для вузов. Екатеринбург: Издательство УГТУ-УПИ, 2005. 617 с.
Арсентьев В. В [и др.] Курс физики. В 2 т. Т. 1: учебник для вузов. СПб. Лань, 2007. 572 с.
Приложение А
Форма отчета по лабораторной работе
ОТЧЕТ
по лабораторной работе 11
Измерение длины волны света с помощью
дифракционной решетки
студент ______________
группа _______________
Дата ________________
Преподаватель _____________
РГППУ
1.Расчетные формулы.
Длина волны света 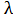 , прошедшего через дифракционную решетку:
, прошедшего через дифракционную решетку:
 , (1)
, (1)
где К – порядок (номер) дифракционного максимума, d – постоянная дифракционной решетки, ak – угол, под которым наблюдается дифракционный максимум К.
Расчет синуса угла ak:
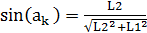 , (2)
, (2)
где L1 – расстояние от дифракционной решетки до экрана, на котором наблюдается дифракционная картина, L2 – расстояние между дифракционным максимумом порядка К и нулевым максимумом (порядок=0) на экране наблюдения дифракционной картины.
Среднее значение длины волны света λср по результатам n измерений:
 , (3)
, (3)
где 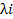 – результат для длины волны света в измерении i.
– результат для длины волны света в измерении i.
Среднеквадратичная погрешность определения длины волны света Sλ по результатам n измерений:
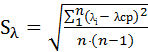 (4)
(4)
Случайная погрешность измерений длины волны света ε λ:
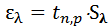 , (5)
, (5)
где 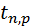 – коэффициент Стьюдента.
– коэффициент Стьюдента.
Систематическая погрешность измерений длины волны света ϴλ :
ϴλ = 0,0325×λср, (6)
где коэффициент 0,0325 рассмотрен в приложении (Б)
Суммарная погрешность измерений длины волны света Δλ:
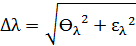 (7)
(7)
Запись окончательного результата:
 нм при p = 0,95 (8)
нм при p = 0,95 (8)
2.Средства измерений и характеристики установки.
Состав экспериментальной установки:
· Источник света (цвет луча света оранжево- красный).
· Дифракционные решетки с числом штрихов на 1мм длины 50, 150, 250.
· Веб-камера.
· Линейки L1 и L2.
· Экран для наблюдения дифракционной картины.
· ПК с монитором для наблюдения и измерений дифракционной картины.
Таблица 1.Средства измерений
| Средство измерения, его тип и номер | Цена деления шкалы | Предел измерения | Предел основной погрешности |
| Линейка L1 | 1 мм | 500 мм | 0,5 мм |
| Линейка L2 | 1 мм | 500 мм | 0,5 мм |
| Экран монитора | 1 пкс | до 1024 пкс | 1 пкс |
3.Схема установки, ход лучей света
(рисунок схемы установки, рисунок хода лучей света после дифракционной решетки)
4.Результаты измерений и математическая обработка результатов измерений.
Таблица 2. Определение масштаба изображения на экране ПК
| Положение метки 1 масштабной линейки L2 | Положение метки 2 масштабной линейки L2 | Расстояние между метками1 и 2 | |||
| пкс (пиксели) | см | пкс (пиксели) | см | пкс (пиксели) | см |
Таблица 3. Определение длины волны света
| Номер максимума (К) | Положение максимума (пиксели) | Расстояние максимума К от нулевого максимума (пиксели) | Расстояние максимума К от нулевого максимума (мм) | sin(ak) | Длина волны света λ (мм) |
| -3 | |||||
| -2 | |||||
| -1 | |||||
| - | - | - | - | - | |
Таблица 4. Обработка результатов измерений длины волны света для нахождения случайной погрешности этих измерений
| Номер результата i | Длина волны λi (нм) | λi - λср | (λi - λср)2 |
| Средняя длина волны λср=… | 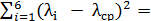 … …
|
Расчеты в таблицах и нахождение длин волн λi … (выполняются в таблицах)
Расчет средней длины волны (так же используется в таблицах):
λср = … (нм)
Расчет среднеквадратичной погрешности измерений
Sλ = … (нм)
Расчет случайной погрешности ελ
ε λ = … (нм) при р=0,95
Расчет систематической погрешности ϴλ
ϴ λ =… (нм)
Расчет суммарной погрешности Δλ
Δλ = … (нм)
Запись окончательного результата 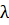
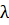 = … (нм) при р=0,95
= … (нм) при р=0,95
(кроме записи результата в нанометрах, продублируйте запись в метрах)
5.Вывод
Приложение Б
Вывод формулы для вычисления систематической погрешности измерения
длины волны света при помощи дифракционной решетки
Исходим из формулы (1) для вычисления длины волны света:
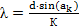 (1)
(1)
Согласно теории оценки погрешностей измерений, получаем выражение для относительной систематической погрешности γ для длины волны света:
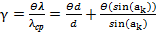 (2)
(2)
где 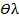 - погрешность определения длины волны света,
- погрешность определения длины волны света,  - средняя длина волны (здесь и далее везде под символом
- средняя длина волны (здесь и далее везде под символом 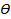 подразумевается систематическая погрешность, а в скобках после символа
подразумевается систематическая погрешность, а в скобках после символа 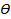 или без них, указывается – чья это погрешность).
или без них, указывается – чья это погрешность).
Относительная погрешность постоянной дифракционной решетки 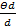 пренебрежимо мала (это исключительно точно выполняемое изделие) и этим слагаемым в формуле (2) можно пренебречь. Тогда из формулы (2) получается выражение (3):
пренебрежимо мала (это исключительно точно выполняемое изделие) и этим слагаемым в формуле (2) можно пренебречь. Тогда из формулы (2) получается выражение (3):
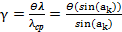 , (3)
, (3)
Таким образом, если найти относительную погрешность для синуса угла ак, то будем знать и величину γ и величину 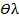 :
:
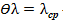 γ (4)
γ (4)
В соответствии с рис.13, получаем следующее выражение для sin(a k):
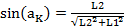 (5)
(5)
Для краткости, обозначим обратный корень 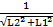 как
как 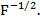 Тогда
Тогда
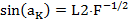 (6)
(6)
С точки зрения теории погрешностей измерений, получим выражение для погрешности синуса 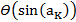 (исходя из формулы (6)):
(исходя из формулы (6)):
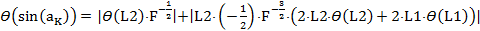 (7)
(7)
или
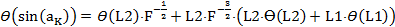 , (8)
, (8)
где 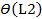 и
и 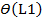 погрешности величин L2 и L1.
погрешности величин L2 и L1.
Умножим правую часть выражения (8) на множитель 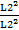 , который не изменит величину этой правой части:
, который не изменит величину этой правой части:
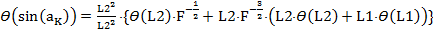 (9)
(9)
Тогда, раскрыв фигурные скобки в правой части уравнения, получим
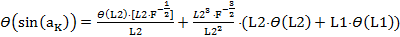 (10)
(10)
С учетом формулы (6), преобразуем выражение (10):
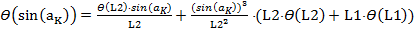 (11)
(11)
Вынесем 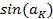 из правой части уравнения (11) в знаменатель левой:
из правой части уравнения (11) в знаменатель левой:
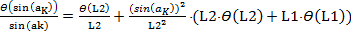 (12)
(12)
Мы получили формулу для относительной погрешности определения синуса. Но в соответствии с уравнением (3), это одновременно и относительная погрешность γ определения длины волны света.
Раскрыв скобки в уравнении (12) и проведя несложные алгебраические преобразования, получим окончательное выражение для γ:
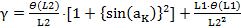 *
* 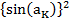 (13)
(13)
Это выражение уже можно проанализировать с точки зрения величины относительной погрешности γ.
В качестве параметра L2 можно взять среднее значение в ряду всех его измерений. Если, например, в работе наблюдались и использовались дифракционные максимумы не более, чем третьего порядка, то в качестве среднего L2 можно взять его значение для максимума с К=2, причем, это еще и среднее значение из двух результатов: L2(k=2) и L2(k=-2). Но эти два результата оказываются взаимосвязаны через общий параметр L0 – координату нулевого максимума:
L2(k=-2) = L0 – L (-2),(14)
L2(k=2) = L (2) – L0, (15)
где L0 – координата нулевого максимума, L (2) – координата максимума с К=2, L (-2) - координата максимума с К=-2, L2(k=-2) и L2(k=2) - расстояние от нулевого максимума до максимума К=-2 и К=2, соответственно. Таким образом, если при определении координаты L0 мы ошибёмся так, что, например, результат для L2(k=-2) окажется заниженным на эту ошибку, то для L2(k=2) результат будет одновременно завышен на эту же ошибку. Тогда среднее значение L2 из результатов L2(k=-2) и L2(k=2) уже свободно от погрешности определения L0, т.к. эта погрешность сама собой компенсируется. В итоге, в погрешности определения расстояния L2 отсутствует погрешность, связанная с определением L0.
Итак, в случае для второго дифракционного максимума, L2 ~ 31 мм (пример из табл.2). Эта величина определяется, в конечном счете, с помощью линейки экрана (рис.9). Погрешность определения координат по этой линейке, с учетом реальных размеров дифракционных максимумов (рис.22, 24) равна, примерно, цене деления данной линейки, т.е. 1мм. Следовательно, получаем отношение 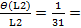 0,0323. Величина
0,0323. Величина 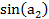 ~ 0,062 (пример из таблицы 2). Тогда для первого слагаемого из выражения (13) получаем следующую оценку:
~ 0,062 (пример из таблицы 2). Тогда для первого слагаемого из выражения (13) получаем следующую оценку:
 ~ 0,0323×[1 + {0,062} 2 ] = 0,0324.
~ 0,0323×[1 + {0,062} 2 ] = 0,0324.
Аналогично рассмотрим второе слагаемое в уравнении (13). Величина L1 фиксирована и равна 50 см или 500 мм. Погрешность шкалы 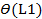 , по которой измеряется параметр L1, можно принять равной 0,5 мм (т.е. половине цены деления шкалы). L2 и
, по которой измеряется параметр L1, можно принять равной 0,5 мм (т.е. половине цены деления шкалы). L2 и 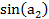 уже известны. Тогда для второго слагаемого из выражения (13) получаем оценку:
уже известны. Тогда для второго слагаемого из выражения (13) получаем оценку:
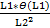 ×
× 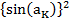 ~
~ 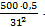 {0.062}2 = 0,0010.
{0.062}2 = 0,0010.
Окончательно, для относительной погрешности γ длины волны света получим:
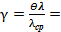 0,0324 + 0,0010 = 0,0325.
0,0324 + 0,0010 = 0,0325.
Приложение С
Справочные данные
Таблица 5. Примеры лазеров и светодиодов, длины волн их излучения
| Вид лазера | Длины волн излучения |
| Аргоновый | 488,0; 514,5 нм, (351; 465,8; 472,7; 528,7 нм) |
| Криптоновый | 416; 530,9; 568,2; 647,1; 676,4 нм |
| Гелий - неоновый | 632,8 нм (543,5; 593,9; 611,8 нм) |
| Азотный | 337,1 нм (316; 357 нм) |
| Красный светодиод | 640-660 нм - обычно не выпускаются яркими |
| Красно-оранжевый светодиод | 630-640 нм - светодиоды в ярких конструкциях |
| Желтый светодиод | 600-620 нм - выпускаются различной яркости |
| Зеленый светодиод | 550-580 нм - неяркие и яркие светодиоды |
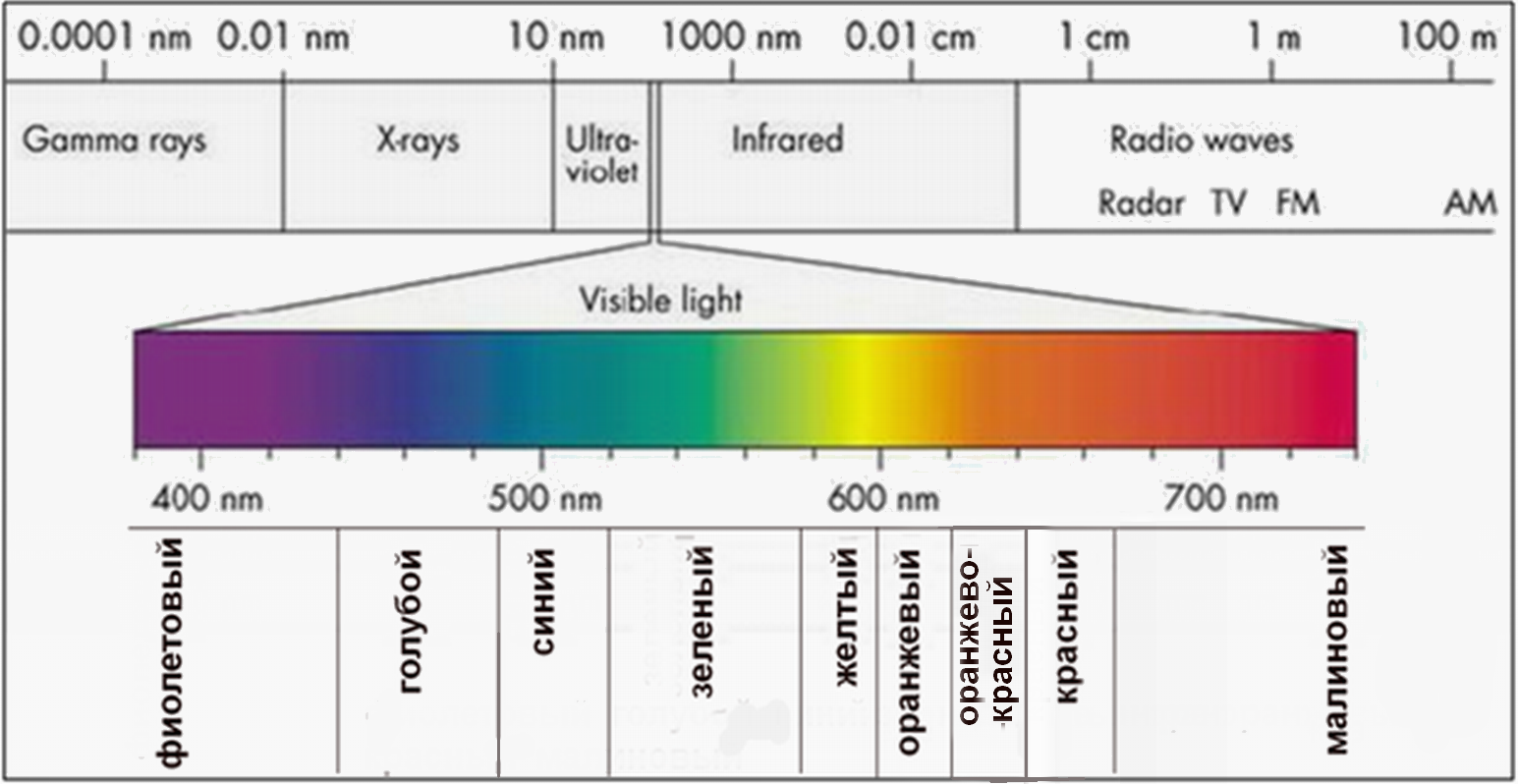
Таблица 6. Шкала электромагнитных волн
Задания и методические указания
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2455; Нарушение авторских прав?; Мы поможем в написании вашей работы!