
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Этап 1. Декомпозиция проблемы и заполнение матриц суждений 1 страница
|
|
|
|
Пример
Рассмотрим задачу оптимизации по двум показателям (частным критериям) I1 и I2. Допустим, что
 , (4.19)
, (4.19)
где х – переменная (ресурс оптимизации).
Свойства решений задач оптимизации по частным критериям.
Задача 1. I1 ® min.
Область определения х Î(-¥, +¥).
Результат:  , то есть абсолютный минимум I1 достигает при х = 0.
, то есть абсолютный минимум I1 достигает при х = 0.
Задача 2. I2 ® min.
Область определения х Î(-¥, -1) и х Î(-1, +¥).
 при e ® 0. При этом I2 ® -¥.
при e ® 0. При этом I2 ® -¥.
На плоскости критериев {I1, I2} = I1´I2 частным решениям задач 1 и 2 соответствуют точки а(1,1) и с(¥, -¥).
Возможные методы получения точек из множества Парето.
I. Метод минимизации одного частного критерия (для данной размерности задачи совпадает с методом последовательных уступок)
| -1 |
| -1 |
| А |
| В |
| I1 |
| I2 |
| Рис. 4.7 |
I1 £ I1* + d1,
где I1* = min I1.
Тогда, как можно видеть из анализа задачи (4.19), существуют два важных случая:
1) При d1 < 1 аргумент может изменяться в пределах х Î(-1, 1). Решение задачи: x = arg{x ® max}, то есть при 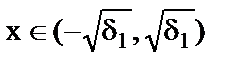 решение будет
решение будет
 и
и  .
.
Случаю х Î(-1, 1) соответствует отрезок кривой между точками А и В (см. рис. 4.7).
2) При d1 ³ 1 решение задачи 2 дает значение х = -1 и I2 = I2*, то есть в точке В решение «срывается» в -¥. Другими словами, при всех d1 ³ 1 существует единственное решение х = -1.
II. Метод сворачивания векторного критерия в глобальный скалярный
Выберем аддитивную форму сворачивания:
 (4.20)
(4.20)
и попытаемся найти экстремум функции классическим методом:
 .
.
Приходим к кубическому уравнению
2.с.х.(х + 1)2 = 1 – с, х ¹ -1 - из (4.20).
Если представить это уравнение в виде
 ,
,
то легко убедиться, что при с = 1 (абсолютный приоритет критерия I1) получается решение х = 0. При с = 0 (приоритет I2) решения не существует.
|
|
|
| -1 |
| d |
| x |
| J |
| Рис. 4.8 |
При некотором с ¹ 0 и с ¹ 1 получается качественно график функции J(x) (см. рис. 4.8). Как видно, при неограниченном диапазоне изменения х решение задачи (4.20) и, соответственно, задачи (4.19) будет х = -1.
Если ограничить x > -1, то решение существует с opt, зависящим от с. Причем при уменьшении с (при с ® 0) точка х = arg{min J} смещается в сторону увеличения.
Для с << 1 примерное решение: 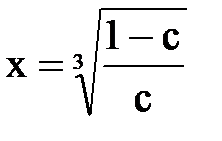 . Например, при с = 0,001 имеем х = 10.
. Например, при с = 0,001 имеем х = 10.
Принятие решения на основе оптимизационной процедуры при известных показателях принципиальных трудностей не вызывает. Неопределенными могут оказаться только приоритеты ЛПР. К сожалению, так бывает очень редко. Обычно имеется неопределенность как в моделях объекта типа Мс, так и в моделях принятия решений (критериях и способах получения решения).
Рассмотрим некоторые виды моделей типа Мт, используемые для принятия решений в более сложных случаях.
К числу таких моделей относится большая группа моделей семиотического типа и группа экспертных методов.
4.5.3. Семиотика – общая теория, исследующая свойства систем знаков, каждому из которых сопоставляется значение. Для семиотического подхода характерны три уровня исследования знаковых систем:
1) синтактика – изучает синтаксис, правила построения и связи в знаковых системах;
2) семантика – изучает интерпретацию, смысл знаковых систем;
3) прагматика – изучает отношения между знаковыми системами и теми, кто их использует.
Теоретическая семиотика изучает совокупность семантики и синтактики, является основой металогики, математических исчислений. Является, в конечном счете, моделью фрагментов мира людей.
В эту группу моделей входят:
- логические модели четкой (конечно-автоматные (КАМ) модели) и нечеткой логики (НЛМ);
|
|
|
- семантические сети (СС);
- продукционные системы (ПС);
- предикатные системы (ПрС) и ряд других.
Рассмотрим некоторые из моделей этой группы.
Логические модели
Конечные автоматы. Логические модели этого типа базируются на алгебре логики. В булевой алгебре используются два элемента «0» и «1» (или {0, 1}).
Примечание: кроме булевой логики имеются также многозначные логики, например, {-1, 0, 1}, а также нечеткие логики, в которых переменные принадлежат значениям 0 и 1 с различной степенью уверенности.
Если используются две переменные Х и Y, принимающие по два значения: 0 = «ложь» и 1 = «правда», то для булевой алгебры определены логические операции (см. табл. 4.1):
Таблица 4.1
| Х | Название логической операции | Обозначение | ||||
| Y | в выражениях | |||||
| - конъюнкция (лог. умножение) | И, AND, &, *, V | |||||
| - дизъюнкция (лог. сложение) | ИЛИ, OR, +, L | |||||
| - тождественность | =, ~ |
А также функция одного операнда - отрицание (функция «НЕ», NOT, «»), например, если Х = 0, то Х = 1.
Существуют и другие функции: стрелка Пирса, штрих Шеффера, импликация и др.
Из булевых переменных и логических операций могут быть построены логические выражения.
Для формирования любой логической формулы достаточно только двух логических операций, одна из которых – отрицание. Для этого применяются законы де Моргана-Шеннона:
 и
и 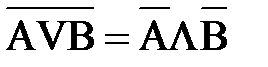 .
.
Для получения логической функции используют таблицу состояния, которая может иметь произвольный вид. Например, см. табл. 4.2.
Таблица 4.2
| X | Y | Z | F |
Для синтеза логической функции существуют две основные формы записи логических выражений:
1) совершенная дизъюнктивная нормальная форма (СДНФ), представляющая собой дизъюнкцию конъюнкций логических переменных; иными словами, логическая сумма слагаемых, каждое из которых является логическим произведением переменных и называется «термом»:
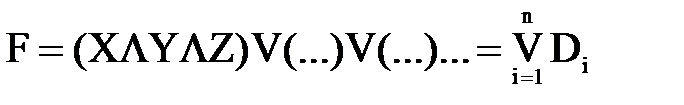 ,
,
где Di – дизъюнкт (терм), n – число дизъюнктов в выражении;
2) совершенная конъюнктивная нормальная форма (СКНФ), представляющая собой конъюнкцию дизъюнкций, иначе называемую записью по нулю:
|
|
|
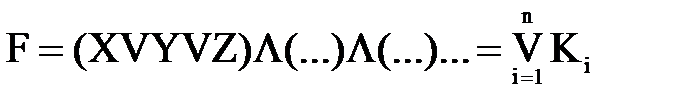 ,
,
где Ki – конъюнкт, n – число конъюнктов.
Правило записи выражения в СДНФ: если в строке, где значение функции равно F = «1», какая-либо переменная принимает значение «1», то эта переменная записывается в дизъюнкт в чистом виде, если принимает значение «0», то с отрицанием.
| Х |
| Х = 1 |
| Х = 0 |
| Y |
| Z |
| 1 терм |
| 2 терм |
| 3 терм |
Рис. 4.9
Правило записи выражения в СКНФ: если в строке, где значение функции равно F = «0», какая-либо переменная принимает значение «0», то эта переменная записывается в конъюнкт в чистом виде, если принимает значение «1», то с отрицанием.
Так, для функции F по табл. Х имеем СДНФ:
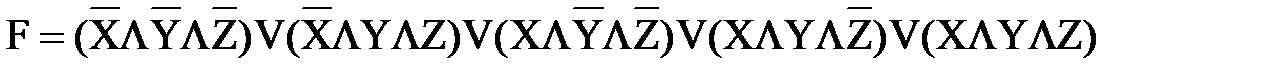
или то же самое в более простой записи:
 .
.
Для упрощения записи логических функций используются:
- логические преобразования,
- карты Карно,
- диаграммы Вейтча,
- методы целенаправленного перебора (алгоритм Мак-Класки).
Рассмотрим метод упрощения полученного логического выражения с помощью карты Карно. Карта Карно представляет собой особый вид таблиц состояний, имеющих прямоугольный вид и состоящих из 2n квадратов, где n – число входных переменных. Стороны карты помечаются именами переменных таким образом, чтобы половина карты соответствовала «1»-му значению переменной, а другая – «0»-му, причем в карте должны быть учтены все возможные сочетания значений переменных (состояния входов). В результате каждая ячейка карты будет соответствовать определенному набору значений входных переменных. В ячейки заносятся соответствующие значения минимизируемой функции. Так, для рассматриваемого примера карта представлена на рис. 4.9.
Далее для записи выражения в СДНФ производятся объединения ячеек карты, содержащих «1» так, чтобы данные ячейки образовывали прямоугольники или квадраты размером 1, 2, 4, 8, 16 и т.д. ячеек. Каждый такой прямоугольник будет соответствовать своему терму, причем, чем он больше, тем проще будет терм. Прямоугольники могут пересекаться.
|
|
|
После этого записываются термы по принципу: если данному прямоугольнику соответствует «1»-е значение какой-либо переменной, то данная переменная входит в терм в чистом виде; если «0»-е значение, то в инверсном; если соответствует как «1»-е, так и «0»-е, то в терм переменная не входит. Наконец, термы объединяются в логическое выражение с помощью функций дизъюнкции. Для рассматриваемого примера получено выражение, состоящее из трех термов:
 .
.
Запись выражений в СКНФ производится аналогично, но объединяются ячейки с нулями. Термы записываются в виде дизъюнкции переменных по принципу: если прямоугольнику соответствует «1»-е значение какой-либо переменной, то данная переменная входит в конъюнкт в инверсном виде; если «0»-е значение, то в чистом; если соответствует как «1»-е, так и «0»-е, то в конъюнкт переменная не входит. После конъюнкты объединяются функциями конъюнкции. Для рассматриваемого примера:
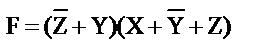 .
.
Из логических выражений подобного вида могут быть образованы логические последовательности, моделирующие процессы принятия решений.
Элементы теории нечетких множеств и нечеткой логики
Нечеткие множества и логические операции на нечетких множествах (далее НС - нечеткие системы) в последнее время стали завоевывать ведущее положение в системах управления, использующих слабоструктурированную, например, лингвистическую информацию. Они позволяют использовать эвристический опыт управления процессами в тех случаях, когда моделирование процессов принятия решений формальными методами не дает удовлетворительного эффекта. В результате появились технические и программные продукты, выпускаемые ведущими мировыми производителями как бытового, так и технологического оборудования.
В частности, расширение языков программирования промышленных контроллеров на базе нечетких систем (Fuzzy Logic Programming) предложено для стандарта IEC 1131.
Нечеткая логика появилась как расширение Булевой логики путем использования логических (нечетких) переменных, принимающих любые значения в интервале [0, 1]. Она была введена доктором Л. Заде (Lotfi Zadeh) в 1960-х годах как способ моделирования неопределенностей естественного языка.
Основная идея Заде состояла в том, что человеческий способ рассуждений в большинстве случаев не может быть описан традиционными математическими формализмами. Основная цель нечеткой логики - моделирование человеческих рассуждений и объяснение человеческих приемов принятия решений в ходе решения различных задач.
| рост, м |
| 0,5 |
| 1,0 |
| 1,5 |
| 2,0 |
| 2,5 |
| mх |
Рис. 4.10
Основным понятием НС является нечеткая логическая переменная х, которой поставлена в соответствие некоторая функция принадлежности m(х),
характеризующая уверенность в принадлежности элемента какому-либо множеству.
| m |
| рост, м |
| m(х1) |
| 1,0 |
| 1,5 |
| 2,0 |
| 2,5 |
| m(х2) |
| m(х3) |
| m(х4) |
| m(х5) |
Рис. 4.11
Существует несколько типовых видов функций принадлежности (см. рис. 4.12):
| а |
| m |
| m |
| а) |
| б) |
| а1 |
| m |
| в) |
| а2 |
| m |
| г) |
| а1 |
| а2 |
| х |
| х |
| х |
| х |
| Рис. 4.12 |
| 1) |
| m(х) = |
| 1, х Î [0, a] |
| 0, х > a |
| (четкая логика); |
| 2) |
| m(х) = exp(-k.x2), k > 0; |
| 3) |
| m(х) = |
| 1, х £ a1 |
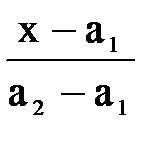 , х Î [a1, a2] , х Î [a1, a2]
|
| 0, x ³ a2; |
| 4) |
| m(х) = |
| 0, х £ a1 |
 , х Î [a1, a2] , х Î [a1, a2]
|
| 1, x ³ a2. |
Пример. Введем переменную х, характеризующую рост человека.
Допустим, что это лингвистическая переменная означает свойство «высокий». Поскольку представления людей о том, какой рост человека считать высоким четко не определены, данная переменная будет являться нечеткой. Интуитивно полученная зависимость ее значения от роста в метрах может иметь, например, вид (рис. 4.10): для характеристики человеческого роста может быть введено множество переменных Х = {х1, х2, х3, х4, х5}, соответствующих значениям: х1 - «очень низкий», х2 - «низкий», х3 – «средний», х4 – «высокий», х5 – «очень высокий». Соответственно переменным определяются функции m(хi), которые могут иметь вид, показанный на рис. 4.11.
Операции над нечеткими множествами:
1) сравнение: А = В, если mА(х) = mВ(х);
2) дополнение (отрицание):  , если mВ(х) = 1 - mА(х);
, если mВ(х) = 1 - mА(х);
3) пересечение АÇВ: mАÇВ(х) = min(mА(х), mB(х));
4) объединение АÈВ: mАÈВ(х) = max(mА(х), mB(х));
5) разность: 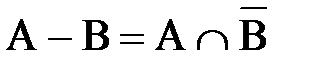 ;
;
6) сумма: mА+В(х) = mА(х) + mB(х) – mА(х)*mB(х);
7) произведение: mА´В(х) = mА(х)*mB(х);
8) концентрация («очень»): mcon(A)(х) = m2А(х);
9) растяжение («довольно»):  .
.
Системами НЛ называются системы, которые оперируют с нечеткими понятиями и используют при этом нечеткую логику. Системы НЛ могут быть классифицированы на три основных типа:
1) простые (pure),
2) системы Токаги и Суджено,
3) системы с фаззификатором и дефаззификатором (fuzzy).
В простых системах используется механизм нечеткого вывода
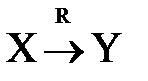 ,
,
где R – композиционные правила.
Недостаток простых систем в том, что входные и выходные переменные являются нечеткими.
Системы Токаги и Суджено. Предлагается выходные переменные взвешивать пропорционально значениям входных.
Системы с фаззификатором и дефаззификатором получаются из простых систем, если перед применением нечетких операций входные переменные фаззифицировать (перевести в нечеткий вид), а после - дефаззифицировать выходные (преобразовать из нечеткого вида в четкий или аналоговый).
Продукционные системы
Наиболее простым с точки зрения построения и широко используемым типом моделей принятия решений являются продукционные системы. Они представляют собой структурированные наборы продукционных правил (ПП) вида
PR = <S, N, F, A Þ C, W>,
где S - сфера применения данного правила; N - номер или имя правила; F - предусловие применения (условие активизации), содержащее информацию об истинности и приоритетности данного правила; A Þ C - ядро ПП; W - постусловие.
Сфера применения S обозначает принадлежность ПП какому-либо определенному этапу функционирования ПС или состоянию процесса принятия решения.
В состав правил могут входить условия активизации F, которые представляют собой либо переменную, либо логическое выражение (предикат). Когда F принимает значение «истина», ядро продукции может быть активизировано. Если F «ложно», то ядро не активизируется.
Постусловие W описывает, какие изменения следует внести в ПС, и актуализируется только после того, как ядро продукции реализовалось.
Интерпретация ядра может быть различной в зависимости от вида А и С, находящихся по разные стороны знака секвенции «Þ». Прежде всего, все ядра делятся на два типа: детерминированные и недетерминированные. В детерминированных ядрах при актуализации ядра и при выполнимости А правая часть ядра выполняется обязательно; в недетерминированных ядрах В может выполняться с определенной вероятностью. Таким образом, секвенция «Þ» в детерминированных ядрах реализуется с необходимостью, а в недетерминированных - с возможностью.
Наиболее часто в ПС используют детерминированные ПП вида
«если А то С»,
где А и С - логические выражения, которые могут включать в себя другие выражения; А называется антецедентом, С - консеквентом.
ПП могут быть доопределены логическими выражениями, определяющими инициируемые процедуры, которые имеют место в случае отсутствия ее активности:
«если А то С1 иначе С2».
Продукционные правила, используемые в СУ, учитывают накладываемые ограничения, а также показатели эффективности, по которым определяются управляющие воздействия и которые часто являются неизмеряемыми лингвистическими переменными.
Достоинствами продукционных систем являются:
- удобство описания процесса принятия решения экспертом (формализация его интуиции и опыта);
- простота редактирования модели;
- прозрачность структуры.
ПС в качестве моделей применимы в следующих случаях:
- не могут быть построены строгие алгоритмы или процедуры принятия решений, но существуют эвристические методы решения;
- существует, по крайней мере, один эксперт, который способен явно сформулировать свои знания и объяснить свои методы применения этих знаний при принятии решения;
- пространство возможных решений относительно невелико (число решений счетно);
- задачи решаются методом формальных рассуждений;
- данные и знания надежны и не изменяются со временем.
Сети Петри
Сети Петри (СП) являются примером семантических сетей, представленных разновидностью ориентированных двудольных графов. Двудольный граф включает вершины двух типов: позиции (обозначаются кружками) и переходы (обозначаются планками). Сеть Петри может быть формально представлена как совокупность множеств:
N = (P, T, G, W),
где P = {p1, p2… pn} – множество всех позиций (n – количество позиций),
Т = {t1, t2… tm} – множество переходов (m – количество переходов),
G = (Gp-t, Gt-p) – множество дуг сети:
Gp-t = (p´t), Gt-p = (t´p) – множества дуг, ведущих соответственно от переходов к позициям и от позиций к переходам (дуг, соединяющих однородные вершины, не существует),
W = {w1, w2… wk} – множество весов дуг (k – количество дуг).
Каждая позиция может быть маркирована, т.е. содержать некоторое число фишек. Если обозначить числа фишек, находящихся в i-й позиции pi, как mi, то маркировка всей сети: M = {m1, m2… mn}. Тогда полное определение сети Петри, включая данные о начальной маркировке, можно записать в виде
PN = (N, M0),
где М0 – начальная маркировка сети.
При моделировании процессов принятия решений с помощью СП ее позиции интерпретируют собой некоторые условия, состояния, значения переменных и т.д. Переходы интерпретируют собой логические предложения (принятие решений), соответствующие выполнению действий, при этом входные позиции – условия выполнения действий, выходные позиции – результат выполнения действий. Действие (переход) связано с принятием какого-либо решения, которое инициировано определенными условиями и результатом которого является новое состояние (условие).
Пример. Схема принятия решений при попытке получить деньги из банкомата (см. рис.4.13).
| Р1 |
| Р2 |
| Р4 |
| Р5 |
| Р8 |
| t1 |
| t4 |
| t3 |
| t8 |
| ● |
| ● |
| Р3 |
| t2 |
| t5 |
| Р6 |
| t9 |
| Р7 |
| t6 |
| t7 |
Рис. 4.13
Смысл позиций: Р1 – карта (ее наличие); Р2 – исправность банкомата; Р3 – введенный код; Р4 – код набран правильно, запрашивается сумма; Р5 – код набран неправильно; Р6 – сумма доступна; Р7 – сумма недоступна (нет такого количества денег на карте); Р8 – деньги (получены). Смысл переходов: t1 – банкомат принимает карту и делает запрос в банк, ввод кода; t2 – запрос суммы; t3 – повторный ввод кода; t5 – выдача сообщения о недоступности суммы; t6 – выдача денег; t7 – повторный набор суммы; t8 – забрать карту из банкомата (другой исход: имеется другая карта, с которой также нужно снять деньги – см. дуги, обозначенные пунктиром); t9 – выдача сообщения, что код неверный. ¨
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 380; Нарушение авторских прав?; Мы поможем в написании вашей работы!