Вычисление средних и полуразностей

Вейвлетные методы

Начнем с одномерного массива данных, состоящего из 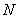элементов. В принципе, этими элементами могут быть соседние пикселы изображения или последовательные звуковые фрагменты. Для простоты предположим, что число 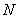равняется степени двойки. Примером будет служить массив чисел (1, 2, 3, 4, 5, 6, 7, 8). Сначала вычислим четыре средние величины , , 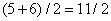и 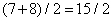. Ясно, что знания этих четырех полусумм не достаточно для восстановления всего массива, поэтому мы еще вычислим четыре полуразност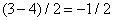и , , и 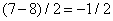, которые будем называть коэффициентами деталей. Мы будем равноправно использовать термины «полуразность» и «деталь». Средние числа можно представлять себе крупномасштабным разрешением исходного образа, а детали необходимы для восстановления мелких подробностей или поправок. Если исходные данные коррелированы, то крупномасштабное разрешение повторит исходный образ, а детали будут малыми.

Массив (3/2, 7/2, 11/2, 15/2, -1/2, -1/2, -1/2, -1/2), состоящий из четырех полусумм и четырех полуразностей, можно использовать для восстановления исходного массива чисел. Новый массив также состоит из восьми чисел, но его последние четыре компоненты, полуразности, имеют тенденцию уменьшаться, что хорошо для сжатия. Воодушевленные этим обстоятельством, повторим нашу процедуру применительно к четырем первым (крупным) компонентам нашего нового массива. Они преобразуются в два средних и в две полуразности. Остальные четыре компонента оставим без изменений. Получим массив (10/4, 26/4, -4/4, -4/4, -1/2, -1/2, -1/2, -1/2). Следующая и последняя итерация нашего процесса преобразует первые две компоненты этого массива в одно среднее (которое, на самом деле, равно среднему значению всех 8 элементов исходного массива) и одну полуразность. В итоге получим массив чисел (36/8, -16/8, -4/4, -4/4, -1/2, -1/2, -1/2, -1/2), который называется вейвлетным преобразованием Хаара исходного массива данных.

Из-за взятия полу разностей вейвлетное преобразование приводит к уменьшению знамений исходных пикселов, поэтому их будет легче сжать с помощью квантования и кодирования длинами серий (RLE), методом Хаффмана, или, быть может, иным подходящим способом. Сжатие с потерей части информации достигается, как обычно, с помощью квантования или простого удаления наименьших полуразностей (заменой их на нули).

Перед тем как двигаться дальше, интересно (и полезно) оценить сложность этого преобразования, то есть, число арифметических операций как функцию размера данных. В нашем примере требуется 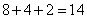операций (сложений и вычитаний). Это число можно выразить как 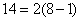. В общем случае, пусть имеется элементов массива. На первой итерации потребуется операций, на второй 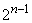операций, и так далее до последней итерации, в которой будет операции. Значит, суммарное число операций равно

.

Таким образом, для совершения преобразования Хаара массива из 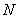элементов потребуется совершить 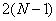арифметических операций, то есть, сложность преобразования имеет порядок . Результат просто замечательный.

Удобно с каждой итерацией процесса связать величину, называемую ее разрешением, которая равна числу оставшихся средних в конце итерации. Разрешение после каждой из трех описанных выше итераций равно , и 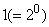. Итак, наш пример вейвлетного преобразования дает массив

.

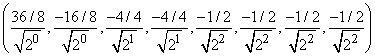Можно показать, что при использовании нормализованного вейвлетного преобразования наилучшим выбором сжатия с потерей будет игнорирование наименьших полуразностей. При этом достигается наименьшая потеря информации.

Две процедуры ниже иллюстрируют, как вычисляется нормализованное вейвлетное преобразование массива из 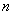компонентов ( 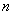равно степени 2).

Обратное преобразование, которое восстанавливает исходный массив.

Эти процедуры, на первый взгляд, отличаются от взятия средних и полу разностей, которые обсуждались выше, поскольку происходит деление на 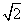, а не на 2. Первая процедура начинается делением всего массива на 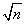, а вторая делает обратное. Окончательный результат, тем не менее, совпадает с массивом, указанным выше. Начиная с массива (1, 2, 3, 4, 5, 6, 7, 8), получаем после трех итераций процедуры NWTcalc следующие массивы

,

,

,

.

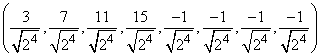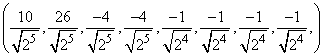Дата добавления: 2014-12-16