
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Автокореляція
|
|
|
|
Якщо дисперсія залишків економетричної моделі є постійною, але має місце кореляція між послідовними значеннями залишків, то це явище називають автокореляцією залишків (не виконується припущення 3 класичної моделі).
Основними причинами автокореляції залишків вважають:
а) кореляцію між послідовними значеннями однієї або декількох пояснювальних змінних;
б) помилкову специфікацію моделі.
Застосування 1МНК у випадку, коли має місце автокореляція залишків, може призвести до таких негативних наслідків:
• оцінки параметрів моделі можуть бути незміщеними, але неефектними (дисперсії оцінок вектора 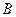 можуть бути невиправдано великими);
можуть бути невиправдано великими);
• статистичні критерії, які використовуються для тестування значущості параметрів і адекватності класичної лінійної моделі, не можна використати, так як при розрахунку вибіркових дисперсій не враховується наявність коваріації залишків;
• так як оцінки можуть бути неефективними, то неефективними виявляться і прогнози в силу великої вибіркової дисперсії.
Нехай економетрична модель представлена як

або
 ,
,  (4.84)
(4.84)
а випадкові величини корелюють між собою і утворюють авторегресійний процес першого порядку (стаціонарний марківський процес першого порядку), тобто
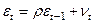 . (4.85)
. (4.85)
У специфікації моделі (4.84) вжито індекс 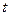 , що вказує на її динамічний характер. Величину
, що вказує на її динамічний характер. Величину 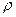 називають коефіцієнтом автокореляції першого порядку (для стаціонарного процесу
називають коефіцієнтом автокореляції першого порядку (для стаціонарного процесу 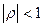 ), а
), а 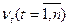 - є послідовністю нормально розподілених випадкових величини з нульовим математичним сподіванням
- є послідовністю нормально розподілених випадкових величини з нульовим математичним сподіванням 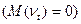 і дисперсією
і дисперсією 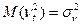 .
.
Процес 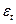 вважається стаціонарним, тому дисперсії не змінюються:
вважається стаціонарним, тому дисперсії не змінюються:
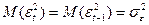 . (4.86)
. (4.86)
Запишемо (4.84) таким чином:
 ,
,
або
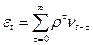 , (4.87)
, (4.87)
де 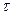 - лаг залишків.
- лаг залишків.
|
|
|
Під лагом розуміють процес, для якого ефект від зміни факторів впливає на зміну результативного показника через певний проміжок часу.
Згідно (4.87) отримуємо дисперсії:
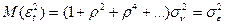 . (4.88)
. (4.88)
Так як  , то
, то
 . (4.89)
. (4.89)
Коваріація залишків запишеться так:
 ;
;
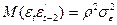 ; (4.90)
; (4.90)
………………….
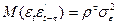 .
.
Коваріаційну матрицю вектора випадкових величин для моделі з автокорельованими залишками можна записати у вигляді:
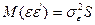 , (4.91)
, (4.91)
де  - матриця коефіцієнтів автокореляції.
- матриця коефіцієнтів автокореляції.
 . (4.92)
. (4.92)
Порівнюючи (4.92) і матрицю  за умови наявності гетероскедастичності, бачимо, що вони суттєво відрізняються, тобто форма третього припущення класичної лінійної моделі при автокореляції залишків інша, чим при гетероскедастичності.
за умови наявності гетероскедастичності, бачимо, що вони суттєво відрізняються, тобто форма третього припущення класичної лінійної моделі при автокореляції залишків інша, чим при гетероскедастичності.
Найпростішим способом виявлення автокореляції залишків є графічний, який полягає у візуальному аналізі кореляційного поля залишків (рис.4.3).
Одним із найчастіше уживаних тестів для перевірки наявності автокореляції між сусідніми членами ряду динаміки слугує тест Дарбіна-Уотсона, ідея якого полягає у такому: якщо кореляція помилок регресії не дорівнює нулю, то вона наявна і в залишках регресії 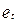 , отриманих у результаті застосування методу найменших квадратів. Тест Дарбіна-Уотсона ґрунтується на використанні d-статистики:
, отриманих у результаті застосування методу найменших квадратів. Тест Дарбіна-Уотсона ґрунтується на використанні d-статистики:
 . (4.93)
. (4.93)
Величину d, яка набуває значень 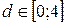 порівнюють з табличними значеннями
порівнюють з табличними значеннями  і
і  , які залежать від рівня значущості
, які залежать від рівня значущості 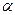 , обсягу вибірки та кількості пояснювальних змінних.
, обсягу вибірки та кількості пояснювальних змінних.
а) б)


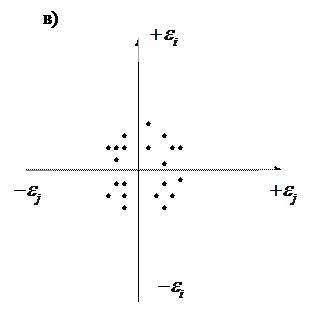
Рис. 4.3. Кореляційне поле залишків: а) – наявність додатної автокореляції; б) – наявність відємної автокореляції; в) – відсутність автокореляції
Можливі випадки (рис.4.4):
а) 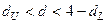 - приймається гіпотеза
- приймається гіпотеза 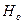 : автокореляція залишків відсутня;
: автокореляція залишків відсутня;
б)  - має місце додатна автокореляція;
- має місце додатна автокореляція;
в) 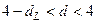 - має місце від’ємна автокореляція;
- має місце від’ємна автокореляція;
г)  або
або 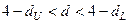 - має місце невизначеність щодо наявності автокореляції.
- має місце невизначеність щодо наявності автокореляції.
В останньому випадку доцільніше прийняти гіпотезу про наявність автокореляції, ніж її відхилити, так як наслідки некоректного прийняття гіпотези про відсутність автокореляції можуть виявитися значно гіршими за некоректне її відхилення.
|
|
|

Істотним недоліком критерію Дарбіна-Уотсона є наявність області невизначеності, а також можливість тестування кореляції лише між сусідніми членами ряду динаміки. Ця обставина призводить до потреби застосування інших тестів на наявність автокореляції, одним з яких є Q-тест Льюінга-Бокса. Статистика цього тесту має такий вигляд:
 . (4.94)
. (4.94)
Гіпотеза 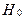 про відсутність автокореляції (або рівність нулю усіх коефіцієнтів автокореляції
про відсутність автокореляції (або рівність нулю усіх коефіцієнтів автокореляції 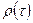 , де
, де 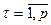 ) відхиляється, якщо значення
) відхиляється, якщо значення  перевищує критичне значення розподілу
перевищує критичне значення розподілу 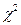 з p ступенями вільності для вибраного рівня значущості.
з p ступенями вільності для вибраного рівня значущості.
Якщо відомий порядок авторегресійної моделі і значення її параметрів, то для оцінювання параметрів економетричної моделі з автокорельованими залишками можна застосувати метод Ейткена (скористатися оператором оцінювання (4.76)). При 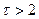 коваріація залишків
коваріація залишків 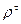 наближається до нуля, а матриця
наближається до нуля, а матриця  має вигляд:
має вигляд:
 . (4.95)
. (4.95)
Ситуації, коли величина 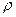 є відомою зустрічаються дуже рідко, тому на практиці її приймають рівною скоригованому циклічному коефіцієнту кореляції:
є відомою зустрічаються дуже рідко, тому на практиці її приймають рівною скоригованому циклічному коефіцієнту кореляції:
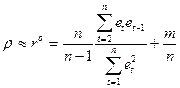 . (4.96)
. (4.96)
Для визначення точкового прогнозу користуються виразом (4.97):
 , (4.97)
, (4.97)
де  - вектор прогнозних значень пояснювальних змінних;
- вектор прогнозних значень пояснювальних змінних;
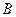 - вектор оцінок параметрів моделі, отриманий за методом Ейткена;
- вектор оцінок параметрів моделі, отриманий за методом Ейткена;
 - залишок
- залишок 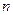 -го періоду, отриманий за допомогою 1МНК.
-го періоду, отриманий за допомогою 1МНК.
Розрахунок інтервального прогнозу проводиться аналогічно випадку, коли має місце гетероскедастичність.
Приклад 4.3. У табл.4.10 подані дані про середньорічні доходи і витрати на споживання в регіоні. Побудувати економетричну модель, що характеризує залежність витрат на споживання від доходів і дослідити її на наявність автокореляції залишків.
Таблиця 4.10
| Рік | ||||||||||
Дохід ( ), тис.грн. ), тис.грн.
| 53,0 | 56,1 | 57,2 | 59,3 | 62,1 | 64,2 | 68,4 | 69,7 | 70,2 | 71,3 |
Витрати на споживання (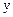 ), тис.грн. ), тис.грн.
| 23,8 | 25,2 | 25,7 | 26,8 | 27,5 | 29,1 | 32,2 | 32,7 | 35,2 | 36,7 |
Застосовуючи 1МНК до даних табл.4.10, отримуємо таку економетричну модель:

Підставимо фактичні дані у рівняння регресії і знайдемо залишки (табл.4.11).
Таблиця 4.11
|
|
|
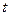
| 
| 
| 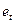
| 
| 
| 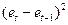
| 
|
| 23,8 | 22,83496 | 0,965039 | 0,9313 | - | - | - | |
| 25,2 | 24,86753 | 0,332466 | 0,110533 | -0,63257 | 0,400149 | 0,320842 | |
| 25,7 | 25,58877 | 0,11123 | 0,012372 | -0,22124 | 0,048945 | 0,03698 | |
| 26,8 | 26,96567 | -0,16567 | 0,027448 | -0,2769 | 0,076676 | -0,01843 | |
| 27,5 | 28,80155 | -1,30155 | 1,694026 | -1,13587 | 1,290207 | 0,215634 | |
| 29,1 | 30,17845 | -1,07845 | 1,163059 | 0,223095 | 0,049772 | 1,403657 | |
| 32,2 | 32,93226 | -0,73226 | 0,536207 | 0,346191 | 0,119848 | 0,789709 | |
| 32,7 | 33,78463 | -1,08463 | 1,176425 | -0,35237 | 0,124164 | 0,794234 | |
| 35,2 | 34,11247 | 1,087534 | 1,182731 | 2,172166 | 4,718303 | -1,17957 | |
| 36,7 | 34,8337 | 1,866299 | 3,483071 | 0,778764 | 0,606474 | 2,029664 | |
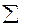
| 294,9 | - | - | 10,31717 | - | 7,434539 | 4,392718 |
Знаходимо оцінку критерію Дарбіна-Уотсона:
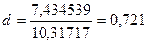 .
.
Для рівня значущості  і
і  з таблиць розподілу маємо:
з таблиць розподілу маємо:
 - нижня межа;
- нижня межа;
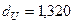 - верхня межа.
- верхня межа.
Так як  , то приймаємо гіпотезу про те, що залишки мають додатну автокореляцію.
, то приймаємо гіпотезу про те, що залишки мають додатну автокореляцію.
Допускаємо, що залишки описуються автокореляційною моделлю першого порядку, і згідно (4.96) отримуємо:
 .
.
Підставляємо значення 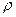 у (4.95) і знаходимо матрицю
у (4.95) і знаходимо матрицю  :
:
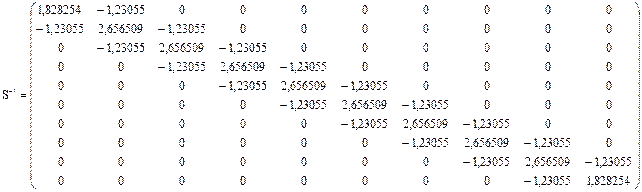
Далі застосовуємо оператор (4.76) і отримуємо таку економетричну модель:
 .
.
На основі побудованої вище моделі згідно методу Ейткена знаходимо розрахункові значення  і залишки (табл.4.12).
і залишки (табл.4.12).
Таблиця 4.12
| 
| 
| 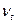
| 
| 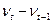
| 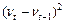
| 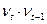
|
| 23,8 | 23,27873 | 0,521268 | 0,271721 | - | - | - | |
| 25,2 | 25,3016 | -0,1016 | 0,010322 | -0,2614 | 0,068329 | -0,05296 | |
| 25,7 | 26,01939 | -0,31939 | 0,10201 | 0,091687 | 0,008407 | 0,032449 | |
| 26,8 | 27,38972 | -0,58972 | 0,347768 | 0,245758 | 0,060397 | 0,18835 | |
| 27,5 | 29,21682 | -1,71682 | 2,947482 | 2,599715 | 6,758517 | 1,012442 | |
| 29,1 | 30,58715 | -1,48715 | 2,211622 | -0,73586 | 0,541491 | 2,553178 | |
| 32,2 | 33,32781 | -1,12781 | 1,271955 | -0,93967 | 0,882973 | 1,677225 | |
| 32,7 | 34,17611 | -1,47611 | 2,178897 | 0,906942 | 0,822543 | 1,66477 | |
| 35,2 | 34,50238 | 0,697622 | 0,486677 | -1,69222 | 2,863608 | -1,02977 | |
| 36,7 | 35,22017 | 1,479831 | 2,1899 | 1,703223 | 2,900969 | 1,032364 | |
| 294,9 | - | - | 12,01835 | - | 14,90723 | 7,078051 |
На основі даних табл.4.12 обчислюємо критерій Дарбіна-Уотсона:
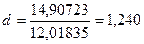 .
.
Так як 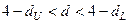 , то можна зробити висновок, що ми позбулися автокореляції залишків.
, то можна зробити висновок, що ми позбулися автокореляції залишків.
Крім методу Ейткена, для оцінювання параметрів моделей з автокорельованими залишками існують інші методи. Так, якщо залишки задовольняють схему авторегресії першого порядку, то для пошуку оцінок параметрів моделі можна використати метод перетворення початкової інформації.
Першим кроком методу перетворення початкової інформації є пошук матриці 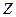 , яка забезпечує отримання скалярної дисперсійної матриці. Нехай матриця
, яка забезпечує отримання скалярної дисперсійної матриці. Нехай матриця 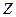 розміру
розміру  має вигляд:
має вигляд:
|
|
|
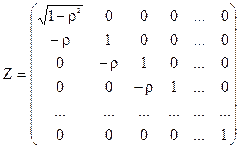 . (4.98)
. (4.98)
Тоді для перетворених даних буде виконуватися умова  (
(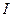 - одинична матриця), а економетрична модель набере вигляду:
- одинична матриця), а економетрична модель набере вигляду:
 . (4.99)
. (4.99)
Оцінювання параметрів моделі (4.99) здійснюють за допомогою 1МНК:
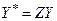 ;
;
 ;
;
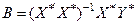 .
.
При цьому результати будуть співпадати із результатами, отриманими згідно методу Ейткена.
В якості матриці, яка використовується для перетворення початкової інформації, можна взяти матрицю  розміру
розміру  , яка отримується з матриці
, яка отримується з матриці 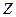 шляхом викреслення першого рядка:
шляхом викреслення першого рядка:
 . (4.100)
. (4.100)
Для визначення невідомих оцінок параметрів економетричної моделі з автокорельованими залишками використовують також ітераційні методи, прикладом яких слугує метод Кочрена-Оркатта.
Розглянемо економетричну модель
 ,
,  , (4.101)
, (4.101)
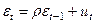 .
.  (4.102)
(4.102)
Після нескладних перетворень отримують модель:
 , (4.103)
, (4.103)
в якій залишки  мають скалярну дисперсійну матрицю.
мають скалярну дисперсійну матрицю.
Запишемо вираз для обчислення суми квадратів залишків у такому вигляді:
 . (4.104)
. (4.104)
Так як у результаті безпосередньої мінімізації (4.104) отримується система нелінійних рівнянь, Кочреном і Оркаттом запропоновано ітеративний метод знаходження невідомих параметрів 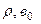 і
і  . Алгоритм методу полягає у виконанні таких кроків:
. Алгоритм методу полягає у виконанні таких кроків:
1. Довільним чином вибирається наближення 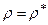 і підставляється в (4.104). У результаті мінімізації (4.104) знаходять початкові наближення
і підставляється в (4.104). У результаті мінімізації (4.104) знаходять початкові наближення  і
і  .
.
2. Значення 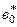 і
і  підставляють у (4.104) і отримують нове наближення
підставляють у (4.104) і отримують нове наближення  .
.
3. З урахуваням  мінімізують суму квадратів залишків (4.104) і обчислюють нові наближення
мінімізують суму квадратів залишків (4.104) і обчислюють нові наближення 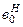 і
і  .
.
4. Якщо нові значення шуканих параметрів (позначені індексом “  ”) відрізняються від попередніх (позначені індексом “
”) відрізняються від попередніх (позначені індексом “  ”) більш як на задану величину, то виконують присвоєння
”) більш як на задану величину, то виконують присвоєння  і
і  і переходять до п.2. У протилежному випадку робота алгоритму вважається завершеною.
і переходять до п.2. У протилежному випадку робота алгоритму вважається завершеною.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 4315; Нарушение авторских прав?; Мы поможем в написании вашей работы!