Выражение одной системы векторов через другую

Опр. 3.1. Пусть 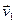, ,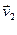…, 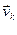(1), 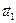, ,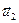…, (2) две системы векторов из V. Говорят, что (1) (линейно) выражается через (2), когда каждый вектор из (1) линейно выражается через (2).

Св-во 3.2. Произвольная подсистема системы векторов выражается через систему.

Доказательство. 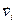= 0 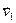+ … + 1 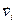+ … + 0 . ■

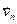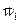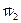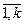
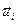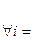
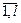
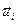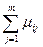
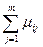
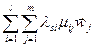Св-во 3.3. Когда система (1) линейно выражается через (2), а (2) линейно выражается через , ,…, (3) тогда (1) линейно выражается через (3). Доказательство. Из того, что система (1) выражается через (2) следует, что "s = = . Из того, что система (2) выражается через (3) следует, что = , из чего получаем: = ( )= = , где .■

Св-во 3.4. Когда (1)- линейно независимая система векторов, а система 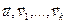линейно зависимая, тогда 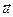линейно выражается через (1). Доказательство. Из линейной зависимости последней системы следует, что = 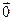, где не все коэффициенты равные нолю. Когда λ=0, тогда (1) - линейно зависимая, что противоречить условию. Из получившегося противоречия следует, что λ 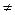0 значит, .■

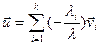5. Максимальные линейно независимые подсистемы (МЛНП)

Опр. 3.5. Подсистема системы 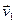, ,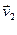…, 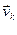(1) называется максимальной линейно независимой подсистемой (МЛНП), когда она не удерживается ни в какой линейно независимой подсистеме, то есть, что 1) (4) - линейно независимая (условие независимости); 2) 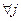, , 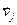-линейно зависимая система (условие полноты).

Св-во 3.6. КРИТЕРИЙ МЛНП. Подсистема (4) системы (1) является МЛНП тогда и только тогда, когда исполняются следующие 2 условия: 1) система (4) линейно независимая; 2) 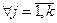. Доказательство. 1) Когда (4) - МЛНП, тогда первое условие, очевидно, исполняется. Когда дополним ее вектором 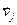, тогда, по определению, она станет линейно зависимой. По свойству 3.4 (Когда (1)- линейно независимая система векторов, а система 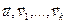линейно зависимая, тогда 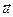линейно выражается через (1)) получаем, что выполняется условие (2), из чего по свойству 3.4 следует, что исполняется условие полноты. 2) Нам надо только доказать, что исполняется условие полноты. Из условия 2) следует, что когда систему (4) пополнить произвольным вектором из системы (1), тогда получится система, в которой один из векторов выражается через остальные. По св-ву эта система является линейно зависимой, что и надо было доказать. ■

Св-во 3.8. Система векторов выражается через свою МЛНП. Доказательство. Следует из 3.6.■

Вывод. 3.9. Две МЛНП системы (1) выявляются одна через вторую. Доказательство. Очевидно из 3.8. Если вся система выражается через МЛНП, то и подсистема выражается через МЛНП. ■

Св-во 3.7. В каждой конечной системе векторов, которая удерживает ненулевой вектор, существует МЛНП.

Доказательство. Возьмем ненулевой вектор 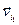. По 2.14 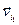- линейно независимая система. Когда построена система 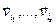, какая линейно независимая, тогда поочередно дополняем ее каждым из остальных вектороВывод Когда есть вектор 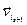, такой, что - линейно зависимая, тогда рассматриваем эту систему и начинаем пополнять ее. Поскольку в (1) конечное количество векторов, этот процесс не может быть бесконечным, значит на каком-то шаге получим подсистему, которая является линейно независимой, и которую нельзя пополнить до линейно независимой подсистемы. Из определения следует, что эта подсистема - МЛНП. ■

Дата добавления: 2014-11-29