
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение, соответствующее плоской электромагнитной волне
|
|
|
|
В НЕОГРАНИЧЕННОЙ СРЕДЕ
ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Плоской электромагнитной волной называется волна, у которой колебания происходят в одной и той же фазе на безграничной плоскости. Иначе говоря, поверхность постоянной фазы (пространственной) такой волны есть бесконечная плоскость. Вид волны определяется постоянной пространственной фазой. Например, практически волну от точечного источника на достаточно большом расстоянии от него можно считать плоской.
Электромагнитные волны бывают однородные и неоднородные. Если поверхность постоянной фазы и поверхность постоянной амплитуды совпадают, то такая волна называется однородной. В противном случае волна называется неоднородной.
Плоская электромагнитная волна имеет такое же важное значение в радиотехнике, как и гармоническое колебание. Математический аппарат значительно упрощается при использовании плоской волны.
Если имеем область, свободную от зарядов (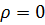 ) и сторонних токов (
) и сторонних токов (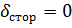 ), то для гармонических ЭДС можно воспользоваться методом комплексных амплитуд. При этом, как нам уже известно, вектор-потенциал удовлетворяет уравнению (1.88) [6], т. е.
), то для гармонических ЭДС можно воспользоваться методом комплексных амплитуд. При этом, как нам уже известно, вектор-потенциал удовлетворяет уравнению (1.88) [6], т. е.
|

где

Этот простейший случай соответствует частному виду решения уравнений Максвелла, дающему плоскую однородную линейно-поляризованную волну. Форма решения уравнения (2.1) в этом случае имеет вид
|
 ,
,
где 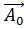 – произвольный постоянный во всем пространстве вектор;
– произвольный постоянный во всем пространстве вектор;
 – некоторая постоянная и в общем случае комплексное число;
– некоторая постоянная и в общем случае комплексное число;
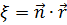 – переменное расстояние вдоль прямой, направление которой определяется направлением единичного вектора
– переменное расстояние вдоль прямой, направление которой определяется направлением единичного вектора  (рис. 2.1);
(рис. 2.1);
 – радиус-вектор, проведённый из начала координат в произвольную точку пространства;
– радиус-вектор, проведённый из начала координат в произвольную точку пространства;
|
|
|
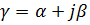 ,
,
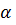 и
и 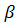 – постоянные числа;
– постоянные числа;
 ,
,
 – координаты вектора
– координаты вектора  .
.
Причём, всегда выполняется условие


|
Рассмотрим процесс, характеризующий решение (2.2),

Это выражение определяет плоскую однородную волну, распространяющуюся вдоль прямой 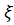 с постоянной фазовой скоростью
с постоянной фазовой скоростью  . А так как
. А так как
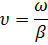
и с изменением времени изменяется и расстояние  , т. е.
, т. е.
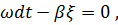
отсюда скорость равна

Форма этой волны плоская, так как пространственная фаза  при
при 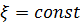 . Но
. Но  есть уравнение плоскости, перпендикулярной
есть уравнение плоскости, перпендикулярной 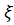 . Амплитуда же волны
. Амплитуда же волны  постоянна тоже при
постоянна тоже при 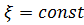 , т. е. мы получили плоскую однородную волну. Амплитуда волны уменьшается с расстоянием по экспоненциальному закону
, т. е. мы получили плоскую однородную волну. Амплитуда волны уменьшается с расстоянием по экспоненциальному закону  .
.
Величина 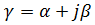 называется постоянной распространения. Её вещественная часть
называется постоянной распространения. Её вещественная часть  определяет затухание амплитуды волны по мере её распространения вдоль прямой
определяет затухание амплитуды волны по мере её распространения вдоль прямой 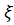 , а мнимая часть
, а мнимая часть 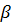 представляет собой волновое число.
представляет собой волновое число.
Поскольку векторы поля  и
и  получаются из вектора
получаются из вектора  простым дифференцированием, проделав операции (1.89) или (1.90) в зависимости от типа волны, то вид зависимостей
простым дифференцированием, проделав операции (1.89) или (1.90) в зависимости от типа волны, то вид зависимостей  и
и  от
от 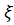 сохраняется таким же, как и выражение (2.2). Таким образом, приняв решение уравнения (2.1) в виде (2.2), мы получим плоскую, однородную, линейно-поляризованную волну.
сохраняется таким же, как и выражение (2.2). Таким образом, приняв решение уравнения (2.1) в виде (2.2), мы получим плоскую, однородную, линейно-поляризованную волну.
В каком же случае решение (2.2) удовлетворяет уравнению (2.1)? Для этого, подставив (2.2) в (2.1), получим:
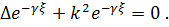
Найдём
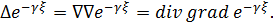
Сначала вычислим 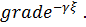
 ;
;
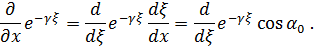
Аналогично вычислим и другие производные. В результате имеем:

В результате вычислений получаем:
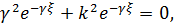 или
или 
При этом должно выполняться условие
|
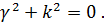
Следовательно,

Таким образом, решение (2.2) удовлетворяет уравнению (2.1), если 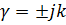 . Отсюда следует, что уравнение (2.1) имеет решение:
. Отсюда следует, что уравнение (2.1) имеет решение:

где  – соответствует прямой волне, т. е. волне, распространяющейся от начала координат вдоль прямой
– соответствует прямой волне, т. е. волне, распространяющейся от начала координат вдоль прямой 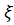 ;
;
 – соответствует обратной (встречной) волне, распространяющейся в отрицательном направлении вдоль прямой
– соответствует обратной (встречной) волне, распространяющейся в отрицательном направлении вдоль прямой  .
.
|
|
|
Перейдём к определению векторов поля  и
и 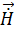 , считая, что
, считая, что 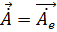 , т. е. берём электрический вектор-потенциал, что соответствует полю электрического типа. (Это поле ничем не отличается от магнитного, за исключением того, что поляризация у них будет разная):
, т. е. берём электрический вектор-потенциал, что соответствует полю электрического типа. (Это поле ничем не отличается от магнитного, за исключением того, что поляризация у них будет разная):
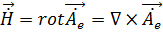 ;
; 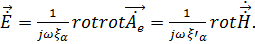
 ,
,
где
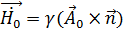 .
.
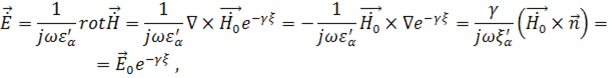

Таким образом, получили:
|

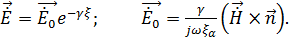
Так как 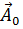 произвольный по величине и направлению вектор, то
произвольный по величине и направлению вектор, то 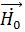 также произвольный по величине вектор, а по направлению перпендикулярен вектору
также произвольный по величине вектор, а по направлению перпендикулярен вектору  , т. е. направлению распространения. Следовательно, если мы задали направление распространения
, т. е. направлению распространения. Следовательно, если мы задали направление распространения  , то вектор
, то вектор  также перпендикулярен этому направлению распространения. Вектор
также перпендикулярен этому направлению распространения. Вектор  также перпендикулярен вектору
также перпендикулярен вектору  и, кроме того,
и, кроме того,  перпендикулярен вектору
перпендикулярен вектору  .
.
Таким образом, в найденной нами плоской волне характерным является то, что векторы  и
и  взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения.
взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения.
 Электромагнитные волны, обладающие таким свойством, называются полностью поперечными и обозначаются Т-волны (или
Электромагнитные волны, обладающие таким свойством, называются полностью поперечными и обозначаются Т-волны (или  - волны). Нетрудно установить расположение этих векторов (рис. 2.2). Эта волна распространяется к нам из-за плоскости чертежа. Из окончательных выражений для векторов поля вектор-потенциал можно исключить. Для этого вычислим векторное произведение
- волны). Нетрудно установить расположение этих векторов (рис. 2.2). Эта волна распространяется к нам из-за плоскости чертежа. Из окончательных выражений для векторов поля вектор-потенциал можно исключить. Для этого вычислим векторное произведение 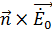
|

Известно тождество
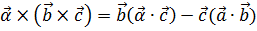 ,
,
поэтому

Следовательно,
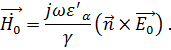
Учитывая это, запишем общее решение уравнений Максвелла для плоской волны:
|
 ;
;
 ,
,
где



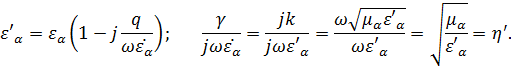
Величина 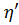 называется характеристическим сопротивлением пространства и весьма широко применяется в инженерных расчётах.
называется характеристическим сопротивлением пространства и весьма широко применяется в инженерных расчётах.
|
|
|
|
|
Дата добавления: 2014-11-28; Просмотров: 667; Нарушение авторских прав?; Мы поможем в написании вашей работы!