
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Установившийся режим в длинных линиях с потерями
Рассмотрим наиболее важный и часто встречающийся на практике случай установившегося режима в длинной линии с потерями, когда источником возбуждения является генератор гармонических колебаний. Поскольку ЭДС возбуждающего генератора изменяется во времени по гармоническому закону, то анализ процессов в длинной линии удобно проводить, используя метод комплексных амплитуд. Этот метод, как известно, позволяет напряжение и ток представить в виде:
|

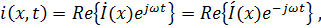
где 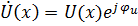 – комплексная амплитуда напряжения;
– комплексная амплитуда напряжения;
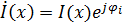 – комплексная амплитуда тока;
– комплексная амплитуда тока;
 – начальные фазы напряжения и тока;
– начальные фазы напряжения и тока;
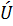 ,
,  – комплексно-сопряжённые амплитуды напряжения и тока.
– комплексно-сопряжённые амплитуды напряжения и тока.
Выражения для текущих комплексных значений напряжения и тока можно записать в виде:
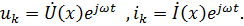
Подставляя эти выражения в уравнения (7.3), которые будут справедливы и для значений 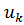 , и
, и  , получим:
, получим:
|
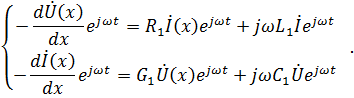
Сократив на общий множитель 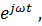 получим:
получим:
|

где  – полное сопротивление единицы длины линии;
– полное сопротивление единицы длины линии;
 – полная проводимость единицы длины линии;
– полная проводимость единицы длины линии;
 и
и 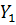 – первичные параметры длинной линии.
– первичные параметры длинной линии.
Заметим, что в системе уравнений (7.15) имеют место полные производные, а не частные, так как в дифференциальных уравнениях в комплексных амплитудах зависимость от времени отсутствует.
Теперь нужно решить систему (7.15). Для этого продифференцируем уравнения по 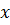 :
:

Подставив в эти выражения значения  и
и  из (7.15), находим:
из (7.15), находим:
|
 .
.
|
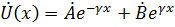 ,
,
где 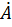 и
и 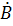 – постоянные интегрирования, в общем случае комплексные величины:
– постоянные интегрирования, в общем случае комплексные величины:
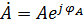 ;
;  ;
;
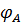 ,
,  – начальные фазы;
– начальные фазы;
 – постоянная распространения, комплексное число.
– постоянная распространения, комплексное число.
Из уравнений (7.16) также следует, что
|

где  – коэффициент затухания;
– коэффициент затухания;
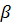 – фазовый коэффициент.
– фазовый коэффициент.
Выражения для тока получим из 1-го уравнения (7.15)
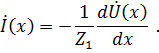
Подставив в эту зависимость значение 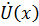 из (7.17), находим:
из (7.17), находим:
|
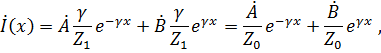
где
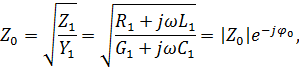
– характеристическое сопротивление длинной линии с потерями;
 и
и  – вторичные параметры длинной линии.
– вторичные параметры длинной линии.
Таким образом, получены общие решения для напряжения 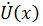 и тока
и тока 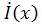 в комплексной форме.
в комплексной форме.
Рассмотрим физический смысл полученных решений. Для этого, используя выражения (7.13), запишем мгновенные значения напряжения и тока в линии:
 .
.
Подставив значения 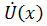 и
и 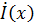 из (7.17) и (7.19), получим:
из (7.17) и (7.19), получим:

|

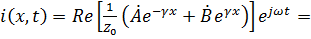
|
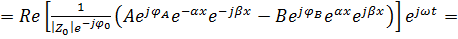
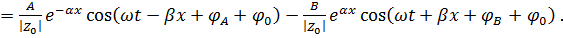
Первые члены в выражениях (7.20) и (7.21) представляют прямые или падающие волны напряжения и тока, причём по мере распространения амплитуда волны затухает по экспоненциальному закону, определяемому множителем 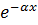 .
.
Рассмотрим, например, падающую волну напряжения. Эта волна распространяется с фазовой скоростью 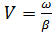 . Если начальная фаза
. Если начальная фаза  , то
, то

Отсюда видно, что  имеет размерность скорости
имеет размерность скорости

где 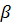 – фазовый коэффициент или волновое число;
– фазовый коэффициент или волновое число;
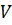 – фазовая скорость;
– фазовая скорость;
 – время запаздывания, т. е. время, необходимое для прохождения волны до текущей точки с координатой
– время запаздывания, т. е. время, необходимое для прохождения волны до текущей точки с координатой 
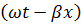 – пространственно-временная фаза.
– пространственно-временная фаза.
Второй член даёт волну, распространяющуюся к генератору от конца линии, и она называется отражённой или обратной волной. Эта волна также затухает по экспоненциальному закону, определяемому множителем 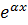 .
.
Таким образом, в линии существует суперпозиция волн падающих и отраженных:
|

Причем существует связь
|

Уменьшение амплитуд напряжения и тока в линии происходит за счёт потерь энергии на нагревание проводов  и потерь в диэлектрике
и потерь в диэлектрике  . Скорость убывания этих амплитуд определяется коэффициентом
. Скорость убывания этих амплитуд определяется коэффициентом 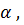 называемым коэффициентом затухания.
называемым коэффициентом затухания.
Из выражений для  ,
,  и
и 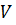 следует, что эти величины в общем случае зависят от частоты. Это нежелательно, так как при передаче сигналов по линии может произойти искажение их спектра, а в конечном итоге и самого сигнала. Поэтому к длинной линии предъявляются требования вносить в передаваемый сигнал минимум искажений. Это требование вместе с требованием малых потерь является основным.
следует, что эти величины в общем случае зависят от частоты. Это нежелательно, так как при передаче сигналов по линии может произойти искажение их спектра, а в конечном итоге и самого сигнала. Поэтому к длинной линии предъявляются требования вносить в передаваемый сигнал минимум искажений. Это требование вместе с требованием малых потерь является основным.
Например, для идеальной длинной линии, у которой 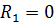 ;
;  , имеем из (7.18):
, имеем из (7.18):

Отсюда видно, что 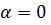 , a
, a 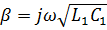 ,
,  , т. е. для идеальной линии фазовая скорость не зависит от частоты.
, т. е. для идеальной линии фазовая скорость не зависит от частоты.
Из (7.19) следует, что
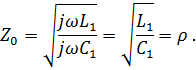
т. е. характеристическое сопротивление равно волновому и тоже не зависит от частоты.
Таким образом, в идеальной длинной линии искажений сигнала не будет.
Рассмотрим, при каких условиях реальные длинные линии являются неискажающими. Неискажающие длинные линии – это реальные длинные линии, для которых выполняются определённые условия. Определим  ,
,  и
и 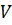 такой линии:
такой линии:
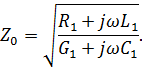
Если выполняется условие
|
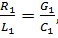
то  , т. е. в этом случае характеристическое сопротивление также не зависит от частоты и равно волновому сопротивлению линии. Условие (7.24) называется условием неискажающей длинной линии:
, т. е. в этом случае характеристическое сопротивление также не зависит от частоты и равно волновому сопротивлению линии. Условие (7.24) называется условием неискажающей длинной линии:


Сравнивая полученный результат для  с выражением (7.18), замечаем, что
с выражением (7.18), замечаем, что
 ,
,
а фазовая скорость

Отсюда видно, что при выполнении условия (7.24) коэффициент затухания  фазовая скорость
фазовая скорость 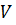 и характеристическое сопротивление
и характеристическое сопротивление  не зависят от частоты.
не зависят от частоты.
Таким образом, в данном случае линия ослабляет сигнал, так как  , но не искажает его.
, но не искажает его.
Рассмотрим наиболее часто встречающийся на практике вид длинной линии – коаксиальный (радиотехнический) кабель. Он применяется при передаче сигналов, когда необходимо иметь малые искажения. В этом случае должны выполняться условия
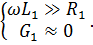
На практике данные условия выполняются достаточно хорошо для требуемого диапазона частот.
Определим при этих условиях  ,
,  и
и 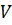 . Из (7.19) имеем:
. Из (7.19) имеем:

Аналогично найдём 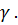

Сравнивая полученный результат с (7.18), замечаем, что  , а фазовая скорость
, а фазовая скорость

т. е. 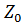 ,
, 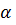 и
и 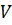 не зависят от частоты.
не зависят от частоты.
Таким образом, в данном случае искажений практически не будет, но сигнал получаем ослабленный, так как 
|
|
Дата добавления: 2014-11-28; Просмотров: 1557; Нарушение авторских прав?; Мы поможем в написании вашей работы!