Скалярное и векторное поля

Пространство (или часть пространства) называется полем, скалярным или векторным, если с каждой точкой его связывается значение некоторого скаляра или вектора.

Каждую точку поля можно определить её радиус-вектором . Следовательно, скалярное или векторное поле буде задано, если каждому радиус-вектору будет приведено в соответствие значение некоторой скалярной функции φ(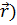 или некоторой вектор-функции 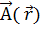. Таким образом, в рассматриваемом случае независимой переменной является радиус-вектор .

Аналитически задание скалярной функции φ(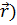 сводится к заданию функции φ(x, y, z) от трёх координат точки, а задание векторной функции 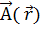– к заданию трёх скалярных функций A_x (x, y, z), A_y (x, y, z) и A_z (x, y, z), являющихся компонентами вектора .

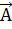Может случиться, что поля меняются с течением времени. Тогда они определяются скалярной или векторной функциями вида

φ(

.

Меняющиеся с течением времени поля называются переменными или нестационарными; поля, не меняющиеся с течением времени, называются постоянными или стационарными.

Для наглядности представления как стационарные, так и нестационарные (для данного момента времени) поля могут быть изображены графически. Допустим скалярное поле задано скалярной функцией φ(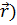 или, что тоже, функцией φ(x, y, z). Если отметить все точки поля, в которых функция φ( 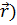имеет одно и то же значение φ₀, то эти точки, вообще говоря, заполнят векторную поверхность или несколько разделённых поверхностей, называемых поверхностями уровня или изоповерхностями.

Очевидно, уравнением любой изоповерхности в декартовых координатах будет φ(x, y, z) = const.

Если провести изоповерхности функции φ(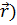, отвечающие равноотстоящим значениям функции φ, то получится картина, указывающая ряд важных свойств изучаемого поля. Так, например, места сближения двух последовательных изоповерхностей указывают на более быстрое изменение здесь функции.

Очевидно, наиболее быстрое изменение функции φ(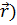 происходит в направлении, перпендикулярном изоповерхности, в то время как при перемещении вдоль самой поверхности значение функции совсем не меняется.

Для наглядного изображения векторного поля 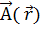вводятся векторные линии, во всякой точке которых вектор 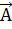имеет направление касательной к этой линии.

Направление касательной к векторной линии в точке M(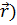 совпадает с направлением приращения 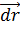вектора при перемещении вдоль линии. Так как по определению векторной линии направления касательной и вектора 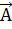должны совпадать в каждой точке линии, можем написать уравнение векторной линии в следующей векторной форме

.

Это приводит к дифференциальному уравнению векторной линии

где A_x(x, y, z), A_y(x, y, z) и A_z(x, y, z) – составляющие вектора .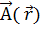

Ориентировка векторных линий, нанесённых на чертёж, указывает направление вектора в каждой точке поля, а по их густоте можно оценить и величину вектора. Для этого нужно провести векторные линии достаточно густо и так, чтобы число этих линий нормально пересекающих единичную площадку, было пропорционально величине вектора.

Дата добавления: 2014-11-28