Решение уравнения механических незатухающих колебаний

Дифференциальные уравнения с

разделяющимися переменными

Простейшим дифференциальным уравнением является уравнение вида

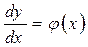. (1.63)

Для отыскания общего решения уравнения (1.63) нужно взять интеграл

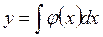(1.64)

или

y = F (x) + C (1.65)

где F(x) -первообразная функции .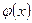

Если задано начальное условие , то для отыскания частного решения нужно определить постоянную интегрирования С из равенства у₀ = F (x ₀)+ С. Уравнениявида (1.63) широко представлены в механике.

Уравнением с разделяющимися переменными называется дифференциальное уравнение, приводящееся с помощью алгебраических преобразований к уравнению вида

f (x) dx = φ (y) dy. (1.66)

Уравнение (1.66) называется уравнением с разделенными переменными.

Для отыскания общего решения уравнения (1.66) нужно взять интегралы от обеих его частей.

Колебания — процессы и состояния, широко представленные в природе и технике. В курсе механики изучаются незатухающие, затухающие и вынужденные колебания. Уравнение механических колебаний представляет собой запись второго закона Ньютона и является дифференциальным, так как ускорение, входящее в этот физический закон — вторая производная координаты по времени. Это уравнение, вид которого

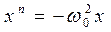, (1.67)

не является дифференциальным уравнением с разделяющимися переменными.

Как более двухсот лет назад получили его решение вида

x (t) = Asin (ω₀ + φ ₀)? (1.68)

Оказывается, подбором.

Заметили, что решением (1.68) уравнения (1.67) должна быть функция, вторая производная которой совпадает с исходной функцией, взятой с обратным знаком. Такому условию удовлетворяют функции синус и косинус, переходящие друг в друга при изменении аргумента на 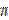/2. Действительно, вторая производная функции x (t) = sint, согласнотаблице производных (Таблица 1) равна

x "(t)= (sin t)" = (cos t)' = -sin t = -x (t), (1.69)

и вторая производная функции х = cost, согласно той же таблице,

x" (t) = (cos t) " = (-sin t)' = -cos t = - x (t). (1.70)

В решении (1.68) уравнения (1.67) функцию синус решили умножить на некоторую постоянную A (позже ее назвали амплитудой колебаний), поскольку синус меняется в пределах от —1 до +1, а колебания могут иметь любой размах. Также методом проб и ошибок в решение были введены постоянные 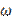₀и ₀.

Приведенные рассуждения показывают, что порой нахождение аналитического решения дифференциального уравнения — это ис­кусство, основанное на общей эрудиции, интуиции и озарении.

Ниже рассмотрим общий метод решения уравнений вида

а₀у"+а ₁ у'+ а ₂ у = 0, (1.71)

к которым и относится уравнение (1.68).

Дата добавления: 2014-11-29