
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статика
|
|
|
|
1.1 Статика абсолютно твердого тіла
Розглядаючи дану тему необхідно вивчити основні поняття і визначення статики: силу, систему сил, рівновагу абсолютно твердого тіла. Звернути увагу на аксіоми статики та їх наслідки. Ознайомитись із видами в’язей і напрямом їх реакцій. Вивчити теорему про три непаралельні сили.
Розглянути приклади розв’язання задач статики.
Завдання: Балка, вагою якої нехтують, закріплена на опорі А, кінцем В покладена на котки. На балку діє вертикальна сила 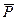 , яка дорівнює 100 Н.
, яка дорівнює 100 Н.
Взявши розміри з малюнку, визначити реакції опор 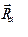 і
і  .
.
Розв’язання:
1. Розглянемо рівновагу балки АВ. (Рис. 1.)
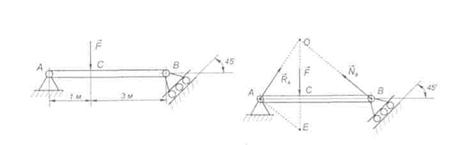
|
Рис. 1. Рис. 2.
2. Покажемо силу 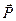 (
(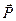 - активна сила).
- активна сила).
3. Звільнимо балку АВ від в'язей, які накладені на неї. Нерухомий  шарнір А і опора на катках В являються в'язями. Реакція
шарнір А і опора на катках В являються в'язями. Реакція 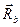 перпендикулярна опорній поверхні. Для знаходження лінії дії реакції шарніра А застосовуємо теорему про три непаралельні сили і знаходимо точку О перетину ліній дії сил
перпендикулярна опорній поверхні. Для знаходження лінії дії реакції шарніра А застосовуємо теорему про три непаралельні сили і знаходимо точку О перетину ліній дії сил 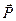 і
і 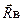 , а почім точку О з'єднуємо з точкою А. Це буде лінія дії реакції
, а почім точку О з'єднуємо з точкою А. Це буде лінія дії реакції 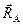 .
.
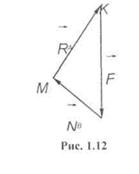
Напрям реакції знаходимо із замкнутого силового трикутника.
4. Будуємо силовий трикутник. Для цього з довільної точки на площині відкладаємо в масштабі силу Е з кінця і початку якої проводимо прямі, паралельні лініям АО і ВО.
5. Одержуємо замкнутий силовий трикутник КDМ (рис. 3). За умови замкнутості силового трикутника виводимо, що реакція 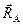 направлена до точки О (реакцію
направлена до точки О (реакцію 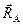 показуємо па рис. 2).
показуємо па рис. 2).
6. Розв'язуємо силовий трикутник. В нашому випадку для розв'язування трикутника даних недостатньо, тому будуємо відомий трикутник, подібний силовому трикутнику. Трикутник АОЕ подібний трикутнику КDМ. З подібності трикутників маємо
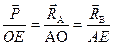
З рис. 2 легко знаходимо, що ОЕ=4 м,
АО = 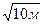 , АЕ =
, АЕ = 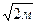 .
.
Звідки:
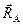 =
= 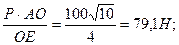
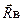 =
= 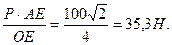
Найкраще матеріал з даної теми висвітлений у навчальному посібнику: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 6 – 17.
Теоретичні відомості
Статика абсолютно твердого тіла.
1. Історія розвитку і зв'язок з іншими дисциплінами. Структура курсу.
2. Основні поняття та визначення.
3. Аксіоми статики та їх наслідки.
4. Теорема про три непаралельні сили.
Література
1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.
2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.
1. Історія розвитку і зв'язок з іншими дисциплінами. Структура курсу.
Технічною механікою – називається наука, що вивчає загальні закони механічного руху матеріальних тіл і встановлює загальні прийоми і методи для вирішення питань, пов'язаних з цим рухом.
Механічний рух – це зміна відносного положення матеріальних тіл в просторі або взаємного положення частин даного тіла, що проходить з часом.
При цьому в класичній (Ньютонівській) механіці розглядаються тіла, розміри яких в багато разів більші міжмолекулярних відстаней і які рухаються зі швидкостями, які значно менші швидкості світла.
Якщо об'єктами досліджень механіки є будь-які реальні тіла: тверді тіла, що деформуються; газоподібні; рідкі; сипучі середовища тощо, то технічна механіка досліджує закономірності руху і виникаючі при цьому взаємодії ідеалізованих тіл: матеріальної точки; системи матеріальних точок; абсолютно твердого тіла. В природі таких ідеалізованих тіл, зазвичай, не існує, однак дані абстракції дозволяють виявити найбільш загальні закони механічного руху, справедливі для руху всіх фізичних тіл незалежно від їх конкретних фізичних властивостей. Тому технічну механіку можна розглядати як основу загальної механіки, яка містить в собі найбільш загальні закони механічного руху, що лежать в основі теорії всіх інших механічних дисциплін: механіки твердих тіл, що деформуються; гідромеханіки; теорії механізмів і машин; деталей машин; будівельної механіки тощо. Величезний вплив механіка, і зокрема, технічна механіка чинила, і продовжує чинити на розвиток і інших фізичних і теоретичних дисциплін: автоматики; телемеханіки; кібернетики тощо.
Механіка є однією з давніх наук, її виникнення і розвиток обумовлені потребами практики. Однак, відомості з механіки, накопичені людством протягом багатьох століть, являли собою, як правило, ряд окремих розрізнених робіт, не зібраних в єдину наукову систему. В створенні такої системи велику роль зіграли праці Галілео Галілея (1564-1642 р.), який вперше сформулював найважливіші поняття механіки: ідеї про інерцію речовини, поняття прискорення, закони складання рухів і швидкостей, закони падіння тіл тощо. З моменту виходу в світ в 1687 р. знаменитої наукової праці Ісаака Ньютона (1643-1727 р.) "Математичні початки натуральної філософії" можна вважати, що механіка дійсно стала наукою. В цій праці Ньютон узагальнив як досвід своїх попередників, так і результати своєї багатогранної наукової діяльності і систематично виклав основні закони класичної механіки.
Подальший розвиток механіки, що опирається на диференціальне і інтегральне числення, пов'язаний з розробкою аналітичних методів, основи яких були закладені в працях Л. Ейлера (1707-1783 р.), Ж. Д’Аламбера (1717-1783 р.), Ж. Лагранжа (1736-1813 р.).
В основу кожного розділу механіки покладені визначення і аксіоми, які випливають з нашого практичного досвіду, і з яких формально логічними міркуваннями одержуються теореми, що є правилами для встановлення закономірностей руху матеріальних тіл.
За характером задач, що розглядаються, технічну механіку поділено на п’ять розділів: статика, кінематика, динаміка, опір матеріалів, деталі машин і механізмів.
Більш детальні відомості про які будуть викладені у відповідних частинах курсу.
2. Основні поняття та визначення.
Статика – розділ механіки, в якому вивчаються методи перетворення сил і з'ясовуються умови рівноваги тіл.
У статиці вирішуються дві основні проблеми:
- заміна системи сил, що діють на тверде тіло, простішою;
- визначення умов рівноваги твердих тіл під дією прикладених до них систем сил.
Cила – міра механічної взаємодії матеріальних тіл, в результаті якої тіла, що взаємодіють можуть надавати одне одному прискорення, або деформуватися.
Така взаємодія є досить різною за своєю фізичною природою. Для розв'язування задач механіки якісна сторона цих різноманітних явищ несуттєва, достатньо охарактеризувати їх з кількісної сторони, користуючись поняттям сили, як деякої універсальної абстракції, в рівній мірі придатної для кількісної оцінки різних механічних взаємодій.
Сила є векторною величиною, яка характеризується:
· напрямом (лінією дії);
· числовим значенням (модулем);
· точкою прикладання.
Сила позначається латинською літерою зі стрілкою над нею. Модуль позначається латинською літерою без стрілки. Для вимірювання величини сили необхідно дати спосіб порівняння довільної сили з деякою одиничною силою. За одиницю сили приймають таку силу, яка масі в 1 кг надає прискорення 1 м/с2, така одиниця сили зветься ньютоном (Н).
Сила 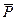 як вектор вважається заданою, якщо визначені її модуль, напрям і точка прикладання. Силу можна задавати графічно або аналітично.
як вектор вважається заданою, якщо визначені її модуль, напрям і точка прикладання. Силу можна задавати графічно або аналітично.
Графічно силу зображують у вигляді вектора з указанням її модуля (абсолютної величини довжини вектора) і напрямку.
Напрямок указується стрілкою, а довжина прямолінійного відрізка в масштабі відповідає довжині вектора.
Матеріальною точкою – називається геометрична точка, якій приписана певна маса-модель матеріального тіла, розмірами якого при певних умовах можна знехтувати.
Система матеріальних точок механічна система ‑ сукупність матеріальних точок, положення і рухи яких взаємопов'язані між собою.
Абсолютно твердим тілом – називається тіло, що складається із системи матеріальних точок, відстань між будь-якими двома його точками залишається незмінною.
Системою сил – називається сукупність сил, що діють на тверде тіло або матеріальну точку.
Розрізняють три системи сил, що діють на тверде тіло у площині й просторі: збіжна система сил, лінії дії яких перетинаються в одній точці; паралельна система сил, лінії дії яких паралельні між собою; довільна система сил, лінії дії яких не паралельні між собою і всі разом не перетинаються в одній точці.
Еквівалентна система сил – така, якою можна замінити систему сил, що діє на тверде тіло, й при цьому характер руху або рівноваги не зміниться. Позначається ”~”.
Pівнодійною 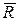 – називається одна сила, яка еквівалентна заданій системі сил
– називається одна сила, яка еквівалентна заданій системі сил  .
.
Зрівноважуюча (або еквівалентна нулю) система сил – така, що залишає в рівновазі матеріальну точку, на яку вона діє.
Зрівноважуюча сила дорівнює за модулем і протилежна за напрямком до рівнодійної сили 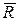 .
.
Матеріальна точка перебуває в рівновазі, якщо вона знаходиться у стані спокою або рівномірного прямолінійного руху – принцип інерції.
Система матеріальних точок перебуває в рівновазі, якщо всі точки системи знаходяться у спокої або рухаються рівномірно, прямолінійно з однаковою швидкістю за величиною і напрямком.
3. Аксіоми статики та їх наслідки.
В основу статики покладені аксіоми, тобто положення, які приймаються без доведення, тому що підтверджуються багатовіковою практикою.
І аксіома. Абсолютно тверде тіло під дією двох сил тільки тоді буде перебувати в рівновазі, коли їх вектори дорівнюють за модулем, протилежні за напрямком і лінії їх дії співпадають.
На рис.1 показане довільне тіло, яке перебуває у стані рівноваги під дією двох сил 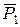 і
і 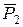 , які мають однакові модулі
, які мають однакові модулі 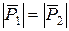 , розташовані на одній прямій
, розташовані на одній прямій 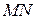 і мають протилежні напрямки. Точки прикладання сил можуть співпадати. Таким чином,
і мають протилежні напрямки. Точки прикладання сил можуть співпадати. Таким чином, 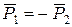 .
.
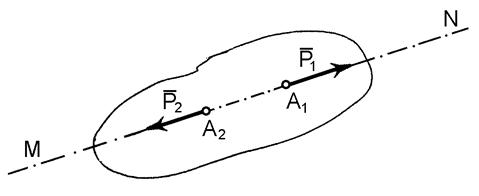
Рис.1
ІІ аксіома. Стан рівноваги тіла не порушиться, якщо до тіла приєднати або відкинути зрівноважену систему сил. Наприклад, систему сил (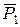 ,
, 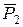 ) на рис.1 Ця аксіома носить назву аксіоми виключення сил.
) на рис.1 Ця аксіома носить назву аксіоми виключення сил.
Наслідок з перших двох аксіом. Точку прикладання сили можна пересувати в межах даного тіла вздовж лінії дії сили (сила є ковзним вектором).
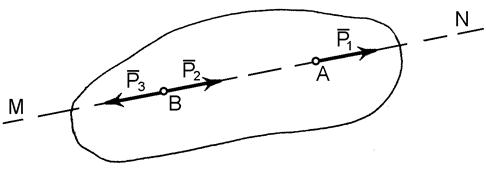
Рис.2
Припустимо, що на тіло (рис.2) діє вектор сили 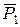 , який прикладений в точці
, який прикладений в точці 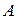 і має лінію дії
і має лінію дії 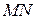 . Прикладемо в довільній точці
. Прикладемо в довільній точці 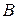 на лінії дії
на лінії дії 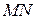 дві сили
дві сили  і
і 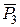 , такі, що
, такі, що  =
= 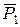 , а
, а 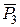 =
= 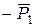 . Згідно першої аксіоми ці сили зрівноважені, а згідно другої аксіоми їх можна приєднати, не змінюючи кінематичного стану тіла.
. Згідно першої аксіоми ці сили зрівноважені, а згідно другої аксіоми їх можна приєднати, не змінюючи кінематичного стану тіла.
Але цю систему трьох сил можна розглядати по іншому: як силу  , яка дорівнює силі
, яка дорівнює силі 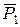 і перенесена з точки
і перенесена з точки 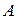 в точку
в точку 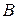 , і зрівноважену систему двох сил (
, і зрівноважену систему двох сил (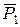 і
і 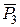 ), яку можна відкинути.
), яку можна відкинути.
ІІІ аксіома. Рівнодійна двох сил, які прикладені до тіла в одній точці, зображується діагоналлю паралелограма, який побудований на цих силах, як сторонах, і прикладена в точці їх перетину. Ця аксіома носить назву закону паралелограма сил.
Рис.3
Припустимо, що до тіла (рис.3) в точці  прикладені дві сили
прикладені дві сили  та
та 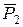 , які розташовані під кутом
, які розташовані під кутом 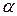 . Побудуємо на цих силах, як на сторонах, паралелограм і проведемо крізь точку
. Побудуємо на цих силах, як на сторонах, паралелограм і проведемо крізь точку 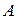 діагональ, яка і буде рівнодійною
діагональ, яка і буде рівнодійною 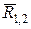 цих сил.
цих сил.
Таким чином, ІІІ аксіома статики дає можливість геометрично додати дві сили, що прикладені в одній точці
 . (1.1)
. (1.1)
З курсу геометрії відомо, що діагональ паралелограма, тобто модуль рівнодійної, дорівнює
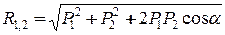 . (1.2)
. (1.2)
Пропонується самостійно визначити рівнодійну, якщо сили прикладені в одній точці і розташовані під прямим кутом, а також коли вони співпадають за напрямком або спрямовані у протилежні сторони.
ІV аксіома. Два взаємодіючих тіла діють одне на одного з рівними за модулем, але протилежними за напрямком силами. Ця аксіома носить назву закону дії та протидії.
Слід зауважити, що сили взаємодії ніколи не зрівноважуються, тому що вони прикладені до різних тіл.
V аксіома. Якщо гнучке (не тверде) тіло перебуває у стані рівноваги під дією системи сил, то цей стан не зміниться, якщо тіло затвердіє. Ця аксіома має назву принципу затвердіння.
4. Теорема про три непаралельні сили.
Теорема: Якщо тіло під дією трьох плоских непаралельних сил перебуває в рівновазі, то лінії дії цих сил перетинаються в одній точці.
Рис.4
Уявимо тіло (рис.4), до якого в точках  прикладені сили
прикладені сили  , вектори яких розташовані в одній площині. Розглянемо спочатку дві сили
, вектори яких розташовані в одній площині. Розглянемо спочатку дві сили 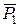 та
та  . На підставі наслідку з І і ІІ аксіом статики вказані сили завжди можна перенести по лінії їх дії в одну точку, наприклад, у точку
. На підставі наслідку з І і ІІ аксіом статики вказані сили завжди можна перенести по лінії їх дії в одну точку, наприклад, у точку 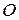 . Далі, якщо маємо в точці
. Далі, якщо маємо в точці 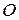 дві прикладені сили, то на підставі ІІІ аксіоми статики їх можна замінити однією силою, тобто рівнодійною
дві прикладені сили, то на підставі ІІІ аксіоми статики їх можна замінити однією силою, тобто рівнодійною 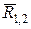 . Побудуємо на рис.4 на вказаних силах
. Побудуємо на рис.4 на вказаних силах 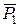 та
та  паралелограм і покажемо рівнодійну
паралелограм і покажемо рівнодійну 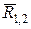 . Тепер тіло буде під дією тільки двох сил
. Тепер тіло буде під дією тільки двох сил 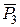 та
та 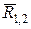 і воно буде в рівновазі лише тоді, коли вектори цих сил розташовані на одній прямій, тобто на прямій
і воно буде в рівновазі лише тоді, коли вектори цих сил розташовані на одній прямій, тобто на прямій 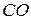 . Тоді і вектор сили
. Тоді і вектор сили 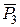 перетинає точку О. Теорема доведена.
перетинає точку О. Теорема доведена.
В результаті вивчення теми слухачі повинні
Знати:
- основні поняття і визначення статики: силу, систему сил, рівновагу абсолютно твердого тіла.
- вивчити теорему про три непаралельні сили.
- види в’язей та напрям їх реакцій.
Вміти:
- розв’язувати задачі статики.
Питання для самоперевірки:
1. Що таке механічний рух? Що вивчає статика?
2. Що вивчає теоретична механіка? Задачі статики.
3. В чому полягає суть понять матеріальна точка та абсолютно тверде тіло?
4. Що таке сила? Які три характеристики має сила?
5. Що таке система сил?
6. Що таке еквівалентна система сил?
7. Яка сила є рівнодійною системи сил?
8. Як формулюються аксіоми статики?
9. В якому випадку матеріальне тіло буде вільним?
10. Як зображується рівнодійна двох сил, які прикладені до тіла в одній точці?
11. Сформулюйте теорему про три непаралельні сили.
Висновок по темі: При розв'язанні задач слід дотримуватися наступної послідовності:
1. Визначити тіло, рівновагу якого слід розглянути в даній задачі.
2. Показати на рисунку всі активні сили, які діють на вибране тіло.
3. Звільнити від в'язей вибране тіло і замінити їх дію силами реакцій в'язей. Зобразити у вигляді векторів усі сили реакцій відкинутих в'язей.
4. Скласти рівняння, яке б виражало умови рівноваги тіла. Тип цих рівнянь визначається характером сил, що діють на тіло.
Зокрема, при розв'язуванні задач з теми "Плоска система збіжних сил" з використанням геометричної умови рівноваги необхідно побудувати замкнутий силовий трикутник. Його побудову необхідно починати з відомої сили, далі за відомими елементами трикутника знайти невідомі величини. Якщо силовий трикутник косокутній, то при розв'язуванні корисно використати теорему синусів, але інколи доцільним є використання умови пропорціональності сторін двох подібних трикутників (силового трикутника і трикутника за основним рисунком).
1.2. Теорія моментів сил
Під час вивчення даної теми необхідно ознайомитись з проекцією сили на вісь і на площину, приведенням збіжних сил до рівнодійної і умовою рівноваги системи збіжних сил.
Вивчити теорію моментів сил: момент сили відносно точки, поняття пари сил, момент пари сил.
Опрацювати приклад розв’язання задач з використанням рівнянь рівноваги системи збіжних сил.
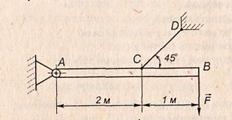
Завдання: Балка АВ підтримується в горизонтальному положенні стержнем СD. Закріплення в точках А, С, D – шарнірні.
Визначити реакції шарніра А і стержня СD, якщо на кінці балки діє вертикальна сила 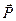 = 5кН. Розміри вказані на рис. Вагою балки нехтуємо.
= 5кН. Розміри вказані на рис. Вагою балки нехтуємо.
|
Розв’язання:
1. Розглянемо рівновагу балки АВ.
2. Показуємо активну силу 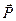 .
.
3. Звільняємо балку від в’язей. В’язями є шарнір А і стержень DC. Дію в’язей заміняємо реакціями. Реакція стержня DC направлена вздовж стержня. Напрям реакції шарніра А знаходимо виходячи з умови, що лінії дії сили 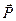 , реакції шарніра А і стержня DC перетинаються в одній точці.
, реакції шарніра А і стержня DC перетинаються в одній точці.
4. Вибираємо осі координат як вказано на рис.
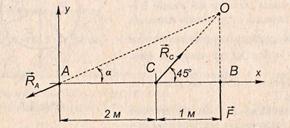
|
5. На балку діє плоска система збіжних сил. Складемо рівняння рівноваги:
∑ Fіх = 0; – RA· cosα + Rc· cos 45o = 0;
∑ Fіу = 0; – F – RA· sinα + Rc· sin 45o = 0.
Звідси:
RA = F/ cosα – sinα; Rc = F· √2 cosα / cosα – sinα.
Оскільки
sinα = 1/√10; cosα = 3/ /√10,
то
RA = 7,9 кН, а Rc = 10,6 кН.
Дана тема найкраще висвітлена у навчальному посібнику: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 20 – 36.
Теоретичні відомості
Теорія моментів сил
1. Проекція сили на вісь і площину.
2. Приведення збіжних сил до рівнодійної.
3. Теорія моментів сил.
Література
1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.
2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.
1. Проекція сили на вісь і площину.
Уявимо силу 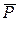 , вектор якої довільно розташований у площині креслення (рис. 1.8). Виберемо у цій площині вісь, наприклад, вісь
, вектор якої довільно розташований у площині креслення (рис. 1.8). Виберемо у цій площині вісь, наприклад, вісь 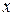 . Необхідно спроектувати вказану силу
. Необхідно спроектувати вказану силу 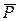 на дану вісь
на дану вісь 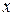 .
.
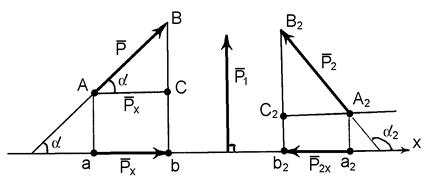
Рис. 1.8
Позначимо спочатку кінці вектора сили 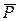 літерами
літерами 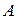 і
і 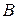 і опустимо з них на вісь
і опустимо з них на вісь 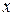 перпендикуляри. Точки перетину перпендикулярів з віссю
перпендикуляри. Точки перетину перпендикулярів з віссю 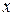 (позначимо їх відповідними малими буквами
(позначимо їх відповідними малими буквами  і
і  ) утворили на осі
) утворили на осі 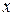 напрямлений відрізок, який і буде проекцією сили
напрямлений відрізок, який і буде проекцією сили 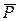 на вісь
на вісь 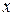 . За величиною цей відрізок дорівнює добутку модуля сили
. За величиною цей відрізок дорівнює добутку модуля сили 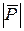 на косинус кута, під яким вектор сили перетинає вісь. А саме:
на косинус кута, під яким вектор сили перетинає вісь. А саме:
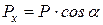 . (1.4)
. (1.4)
За знаком проекція сили на вісь тоді буде додатня, коли кут 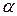 (кут перетину вектора сили або лінії дії сили з віссю) гострий. Цілком зрозуміло, якщо цей кут дорівнює
(кут перетину вектора сили або лінії дії сили з віссю) гострий. Цілком зрозуміло, якщо цей кут дорівнює 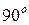 , то проекція сили
, то проекція сили 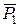 на вісь
на вісь 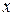 дорівнюватиме нулю. Якщо кут
дорівнюватиме нулю. Якщо кут 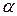 буде тупий, то проекція сили
буде тупий, то проекція сили  на вісь
на вісь 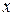 буде мати від'ємний знак.
буде мати від'ємний знак.
Таким чином, проекція сили на вісь – це напрямлений відрізок на осі, утворений між перпендикулярами, які опущені з кінців вектора сили на вісь, і який за величиною дорівнює добутку модуля сили на косинус кута між напрямом вектора сили та віссю.
Спроектуємо тепер вектор сили на площину і осі координат.
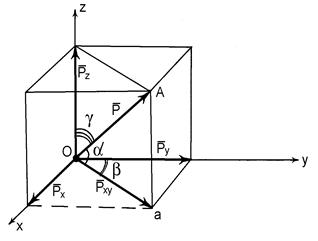
Рис. 1.9
Візьмемо силу  ,вектор якої довільно розташований у просторі (рис. 1.9). Виберемо у просторі прямокутну декартову систему координат
,вектор якої довільно розташований у просторі (рис. 1.9). Виберемо у просторі прямокутну декартову систему координат  , початок відліку якої (точку
, початок відліку якої (точку  ) суміщений з точкою прикладання вектора сили
) суміщений з точкою прикладання вектора сили 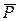 . Спроектуємо вектор сили
. Спроектуємо вектор сили 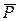 на площину
на площину 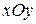 . Опустимо з точки
. Опустимо з точки 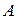 (кінець вектора сили) на вказану площину перпендикуляр, який перетинає її в точці
(кінець вектора сили) на вказану площину перпендикуляр, який перетинає її в точці  . На площині
. На площині 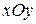 утворено вектор
утворено вектор 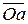 , який і є проекцією
, який і є проекцією 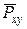 сили на площину. За модулем ця проекція дорівнюватиме
сили на площину. За модулем ця проекція дорівнюватиме
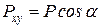 , (1.5)
, (1.5)
де 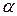 - кут між вектором сили
- кут між вектором сили 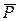 та площиною
та площиною 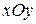 .
.
Якщо в площині 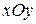 позначити кут
позначити кут 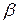 , то є можливість спроектувати силу
, то є можливість спроектувати силу 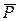 на осі
на осі 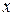 та
та 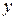 , опускаючи з точки
, опускаючи з точки  на осі перпендикуляри і за відомим вже правилом отримати проекції вектора
на осі перпендикуляри і за відомим вже правилом отримати проекції вектора 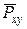 на вказані осі:
на вказані осі:
 , (1.6)
, (1.6)
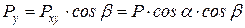 . (1.7)
. (1.7)
У даному випадку крізь вісь 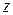 та вектор сили
та вектор сили 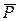 можна провести площину, тому є можливість спроектувати силу на цю вісь за відомим правилом. Ця проекція буде дорівнювати
можна провести площину, тому є можливість спроектувати силу на цю вісь за відомим правилом. Ця проекція буде дорівнювати
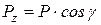 , (1.8)
, (1.8)
де 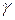 - кут між вектором сили
- кут між вектором сили 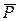 та віссю
та віссю 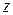 .
.
Визначення сили за її проекціями
Припустимо, що маємо в площині рисунка прямокутну декартову систему координат 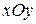 , задані дві проекції сили –
, задані дві проекції сили – 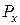 та
та 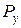 (рис. 1.10). Треба за даними проекціями обчислити модуль вектора самої сили
(рис. 1.10). Треба за даними проекціями обчислити модуль вектора самої сили 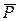 , а також його напрямок.
, а також його напрямок.
На заданих проекціях, як на сторонах, будуємо прямокутник, діагональ якого, що проходить крізь точку перетину проекцій, і є шуканим вектором сили 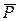 . Модуль сили
. Модуль сили 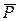 можна визначити з наступного виразу:
можна визначити з наступного виразу:
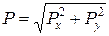 . (1.9)
. (1.9)
Кути між вектором сили 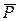 та осями
та осями  та
та  можна визначити за допомогою напрямних косинусів
можна визначити за допомогою напрямних косинусів
 (1.10)
(1.10)
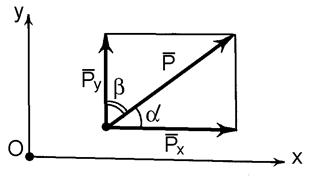
Рис. 1.10
2. Приведення збіжних сил до рівнодійної.
По характеру розташування всі системи сил можна поділити на плоскі і просторові системи. Крім того, кожна з цих систем може бути поділена на систему збіжних сил, систему паралельних сил і систему довільних сил.
– система збіжних сил характеризується тим, що напрямки векторів усіх сил перетинаються в одній точці.
– у системі паралельних сил вектори сил паралельні.
– у системах довільних сил вектори розташовані як завгодно на площині або у просторі.
Таким чином, можна констатувати, що маємо шість різних систем сил, під дією яких тіло може перебувати в стані рівноваги, або рухатись за певним законом.
Теорема про проекцію рівнодійної сили на вісь
Проекція вектора рівнодійної сили на вісь дорівнює алгебраїчній сумі проекцій векторів складових сил на ту ж саму вісь.
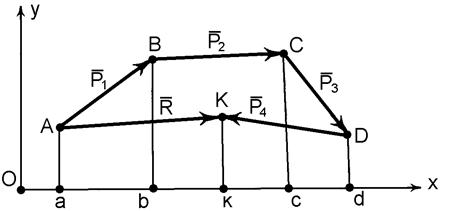
Рис. 1.11
Доведення. Маємо систему сил 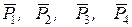 , яка зведена до рівнодійної
, яка зведена до рівнодійної 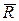 за допомогою силового многокутника (рис. 1.11). Введемо на площині прямокутну декартову систему координат
за допомогою силового многокутника (рис. 1.11). Введемо на площині прямокутну декартову систему координат 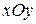 і спроектуємо на вісь
і спроектуємо на вісь 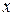 всі сили. Для цього позначимо кінці векторів всіх сил літерами –
всі сили. Для цього позначимо кінці векторів всіх сил літерами – 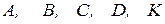 і проведемо перпендикуляри з кожної точки на вісь
і проведемо перпендикуляри з кожної точки на вісь 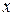 . Точки перетину перпендикулярів з віссю, які позначені відповідними малими літерами –
. Точки перетину перпендикулярів з віссю, які позначені відповідними малими літерами – 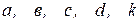 , утворили на осі напрямлені відрізки, які і є проекціями всіх сил на вісь. Кожна проекція, відповідно, дорівнює
, утворили на осі напрямлені відрізки, які і є проекціями всіх сил на вісь. Кожна проекція, відповідно, дорівнює
 . (1.11)
. (1.11)
Додамо алгебраїчно всі проекції і підрахуємо, чому ця сума дорівнює:
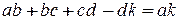 . (1.12)
. (1.12)
Але відрізок 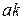 і є проекцією рівнодійної сили
і є проекцією рівнодійної сили 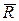 на вісь
на вісь 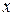 . Поширюючи цю суму на п сил, можна записати:
. Поширюючи цю суму на п сил, можна записати:
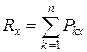 . (1.13)
. (1.13)
Теорема доведена.
Аналітичний спосіб додавання системи збіжних сил
На підставі теореми про проекцію рівнодійної сили на вісь, маємо:
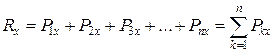 . (1.14)
. (1.14)
Аналогічно проекція рівнодійної сили на вісь 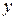 буде дорівнювати
буде дорівнювати

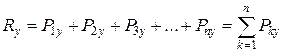 . (1.15)
. (1.15)
Модуль рівнодійної дорівнює
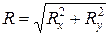 . (1.16)
. (1.16)
Кути між вектором рівнодійної 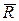 та осями координат
та осями координат 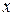 та
та 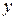 визначимо через косинуси кутів між відповідною віссю та рівнодійною:
визначимо через косинуси кутів між відповідною віссю та рівнодійною:
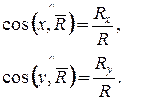 (1.17)
(1.17)
3. Теорія моментів сил.
Обертальний ефект сили характеризується її моментом відносно центра (точки), а також і відносно осі (останній буде далі).
Розглянемо довільне тіло (рис.1.14), яке може повертатися навколо точки 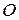 (точніше навколо осі, яка перпендикулярна площині рисунка і проходить через точку
(точніше навколо осі, яка перпендикулярна площині рисунка і проходить через точку 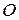 ). Прикладемо в інших точках тіла
). Прикладемо в інших точках тіла 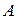 ,
, 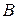 ,
, 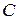 сили
сили 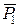 ,
, 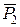 ,
, 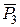 і визначимо спочатку, чи зможуть вони повертати тіло навколо точки
і визначимо спочатку, чи зможуть вони повертати тіло навколо точки 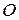 .
.
Як бачимо з рисунка, сила 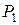 , яка прикладена у точці
, яка прикладена у точці 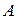 , може повернути тіло навколо точки
, може повернути тіло навколо точки 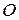 проти ходу стрілки годинника. Сила
проти ходу стрілки годинника. Сила 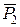 - за ходом стрілки годинника. Проте сила
- за ходом стрілки годинника. Проте сила 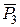 не може повертати тіло навколо точки
не може повертати тіло навколо точки 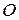 , оскільки лінія дії сили
, оскільки лінія дії сили 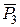 перетинає дану точку. Таким чином сили
перетинає дану точку. Таким чином сили 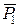 і
і 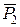 створюють обертальний ефект (момент) відносно точки
створюють обертальний ефект (момент) відносно точки 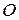 , а сила
, а сила 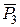 - ні.
- ні.
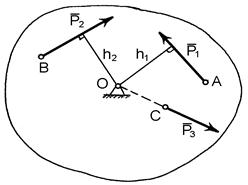
Рис. 1.14
Моментом сили відносно центра (точки) називається взятий з відповідним знаком добуток сили на плече. Плече сили відносно центра – це найкоротша відстань (перпендикуляр) між даним центром і лінією дії сили.
Момент вважається додатнім, якщо сила намагається повернути тіло відносно даної точки проти годинникової стрілки і від'ємним, якщо - за годинниковою стрілкою.
Момент сили  відносно точки
відносно точки  позначається як
позначається як  .
.
Покажемо на рис. 1.14 плечі сил, які створюють моменти відносно точки 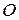 , і визначимо алгебраїчні величини моментів цих сил
, і визначимо алгебраїчні величини моментів цих сил
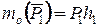 , (1.23)
, (1.23)
 , (1.24)
, (1.24)
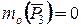 . (1.25)
. (1.25)
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 2217; Нарушение авторских прав?; Мы поможем в написании вашей работы!