
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прискорення руху. 2 страница
|
|
|
|
2. Швидкості точок тіла при плоско паралельному русі.
Теорема: швидкість будь-якої точки плоскої фігури дорівнює векторній сумі швидкості полюса і обертальної швидкості цієї точки навколо полюса.
Маємо плоску фігуру S, яка здійснює складний рух (рис. 4). Швидкість будь-якої точки цієї фігури, зокрема точки В, можна уявити, як векторну суму переносної та відносної швидкостей:
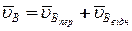 ,
,
де 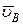 - абсолютна швидкість точки В відносно нерухомої системи координат;
- абсолютна швидкість точки В відносно нерухомої системи координат;  - швидкість точки В у переносному поступальному русі;
- швидкість точки В у переносному поступальному русі; 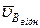 - швидкість точки В у відносному русі, тобто в обертанні навколо полюса (наприклад, точки А).
- швидкість точки В у відносному русі, тобто в обертанні навколо полюса (наприклад, точки А).
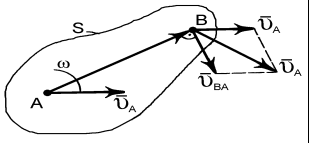
Рис. 4
Оскільки за переносний прийнято поступальний рух фігури S, то переносні швидкості будь-яких точок фігури, зокрема полюса А, однакові, тобто:
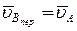 .
.
Величина швидкості у відносному русі, оскільки він є обертальним, дорівнює:
 ,
,
де вектор швидкості 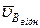 лежить у площині фігури і спрямований перпендикулярно відрізку АВ у бік обертання фігури S.
лежить у площині фігури і спрямований перпендикулярно відрізку АВ у бік обертання фігури S.
Будемо позначати відносну швидкість 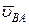 . Це позначення показує, що точка В у відносному русі обертається навколо точки А. Тоді:
. Це позначення показує, що точка В у відносному русі обертається навколо точки А. Тоді:
 .
.
Теорему доведено.
Наслідок: проекції швидкостей двох точок плоскої фігури на лінію, яка проходить через ці точки, рівні між собою.
Розглянемо точки А і В плоскої фігури, яка здійснює складний рух (рис. 5).

Рис. 5.
Приймемо точку А за полюс, навколо якого обертається у відносному русі точка В.
Згідно тільки що доведеної теореми можна записати
 .
.
Розглянемо проекції швидкостей 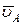 та
та 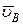 на лінію, яка з’єднує обидві точки:
на лінію, яка з’єднує обидві точки: 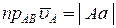 ,
,
 ,
,
але 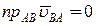 ,
,
оскільки
 .
.
Отже,
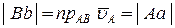 ,
,
тобто
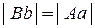 ,
,
або
 .
.
Знаючи модуль  швидкості даної точки
швидкості даної точки 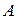 і кут нахилу
і кут нахилу 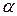 вектора цієї швидкості, а також напрямок вектора шуканої швидкості будь-якої іншої точки
вектора цієї швидкості, а також напрямок вектора шуканої швидкості будь-якої іншої точки 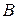 (кут
(кут 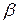 ), можна визначити її модуль, тобто
), можна визначити її модуль, тобто
|
|
|
 .
.
3. Миттєвий центр швидкостей і способи його визначення.
Миттєвим центром швидкостей, називається точка Р рухомої плоскої фігури, швидкість якої в даний момент часу дорівнює нулю.
Вказана точка може бути розташованою або на самій рухомій фігурі, або на її уявному продовженні.
Розглянемо фігуру S, яка здійснює плоский рух (рис. 6). швидкість деякої точки А цієї фігури вважається відомою і дорівнює 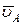 , напрям обертання та кутова швидкість ω обертання фігури теж вважаються відомими і показані на рис. 6.
, напрям обертання та кутова швидкість ω обертання фігури теж вважаються відомими і показані на рис. 6.
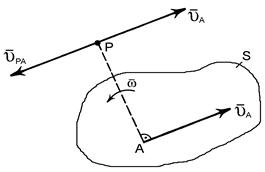
Рис. 6
Зробимо далі таку побудову: опустимо з точки А перпендикуляр до вектора швидкості 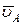 , який напрямлений у бік обертання фігури. Відкладемо на цьому перпендикулярі відрізок довжиною
, який напрямлений у бік обертання фігури. Відкладемо на цьому перпендикулярі відрізок довжиною  . Приймемо точку А за полюс, тоді швидкість точки Р даної фігури буде визначатись за допомогою такого векторного рівняння:
. Приймемо точку А за полюс, тоді швидкість точки Р даної фігури буде визначатись за допомогою такого векторного рівняння:
 .
.
З цього виразу знайдемо швидкість  . Вона буде дорівнювати:
. Вона буде дорівнювати:
 .
.
Вектор швидкості  буде напрямлений протилежно вектору швидкості
буде напрямлений протилежно вектору швидкості 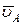 , тобто
, тобто
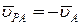 .
.
Тоді, підставляючи це значення швидкості  у вираз для швидкості точки Р, остаточно будемо мати:
у вираз для швидкості точки Р, остаточно будемо мати:
 .
.
Таким чином, швидкість точки  дорівнює нулю, і тим самим доведено існування миттєвого центру швидкостей.
дорівнює нулю, і тим самим доведено існування миттєвого центру швидкостей.
Способи визначення положення миттєвого центру швидкостей
Розглянемо декілька окремих випадків визначення положення миттєвого центру швидкостей. При цьому можуть бути такі випадки (рис. 7):
1. Миттєвий центр швидкостей фігури розташований на перпендикулярі, який проведено до напрямку вектора швидкості деякої точки фігури (рис. 7, а).
2. Миттєвий центр швидкостей фігури може бути знайдено як точку перетину двох перпендикулярів, які поставлені з двох точок фігури до напрямків векторів швидкостей цих точок (рис. 7, б).
3. Якщо вектори швидкостей двох точок фігури паралельні (рис. 7, в), а самі точки не лежать на одному перпендикулярі до напрямків їх швидкостей, то обертання в цей момент відсутнє, і фігура здійснює в даний момент поступальний рух, а швидкості усіх точок фігури дорівнюють одна одній.
|
|
|
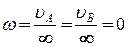 .
.
Додамо, що в цьому випадку, на відміну від поступального руху, прискорення точок будуть різні.
4. Якщо вектори швидкостей двох точок фігури паралельні (рис. 7, г), точки лежать на одному перпендикулярі до напрямків їх швидкостей, а модулі швидкостей не однакові, то миттєвий центр швидкостей міститься у точці перетину прямої, що з’єднує кінці векторів швидкостей з вказаним вище перпендикуляром.

Рис. 7
Тоді, як бачимо з (рис. 7, г), матимемо:
 .
.
5. При коченні фігури без ковзання по деякій нерухомій кривій миттєвим центром швидкостей буде точка дотику фігури з цією нерухомою кривою (рис. 7, д).
6. Кутова швидкість фігури в кожний даний момент часу дорівнює відношенню модуля швидкості будь-якої точки фігури до відстані від цієї точки до миттєвого центру швидкостей.
Теорема про кінцеве переміщення плоскої фігури
Теорема: фігуру в площині П з одного положення в будь-яке інше можна перевести шляхом одного повороту в цій площині навколо точки Р, яка є центром кінцевого обертання.
Припустимо, що в положенні І фігура характеризується відрізком АВ, незмінно зв’язаним з фігурою, а в положенні ІІ цей відрізок займе положення А 1 В 1(рис. 8).
Припустимо, що точка Р є центром обертання, тобто обертання трикутника АВР до положення Δ А 1 В 1 Р 1чиниться навколо точки Р. Оскільки Δ АВР при своєму обертанні не дістає деформації, то Δ АВР = Δ А 1 В 1 Р 1та АР = А 1 Р, ВР = В 1 Р.
Якщо розглядати трикутники АА 1 Р та ВВ 1 Р, то вони рівнобедрені, оскільки АР = А 1 Р, ВР = В 1 Р. Крім цього дані трикутники мають спільну вершину – точку Р.
При врахуванні того, що відомі положення І та ІІ відрізка АВ, то відомі (або можуть бути легко знайдені) відрізки АА 1та ВВ 1. оскільки точка Р є вершиною рівнобедреного трикутника АА 1 Р, то вона лежить на перпендикулярі, який проведений з середини відрізка ВВ 1 (тобто з точки D). Якщо врахувати, що точка Р є спільною, то вона лежить на перетині перпендикулярів, які проведені з середин відрізків, що з’єднують початкове та кінцеве положення відповідних точок відрізка АВ фігури.
|
|
|

Рис. 8.
Таким чином, доведена можливість існування та визначене положення центра кінцевого обертання.
Цілком очевидно, що у випадку відсутності перетину цих перпендикулярів (точніше, якщо вони перетинаються в нескінченності), то центра кінцевого обертання немає (або він теж знаходиться у нескінченності). Це буде можливе у тому і тільки у тому випадку, коли відрізки АВ і А 1 В 1 паралельні, і лінії, що з’єднують їх відповідні точки, взагалі не перетинаються.
В результаті вивчення теми слухачі повинні
Знати:
- кінематичні рівняння руху;
- швидкості точок тіла при плоско паралельному русі;
- прискорення точок тіла при плоскопаралельному русі.
Вміти:
- визначати прискорення точок тіла при плоскопаралельному русі.
Питання для самоперевірки
1. Який рух називається плоским?
2. Напишіть кінематичні рівняння плоского руху.
3. Чи залежить кутова швидкість плоскої фігури від вибору полюса?
4. Яка існує залежність між швидкістю довільної точки плоскої фігури і швидкістю полюса?
5. В чому полягає теорема про проекції швидкостей двох точок плоскої фігури на лінію, що їх з’єднує?
6. Що називається миттєвим центром швидкостей?
7. В чому полягає теорема про існування миттєвого центру швидкостей?
8. Як визначається положення миттєвого центру швидкостей в різних випадках?
9. Що називається миттєво поступальним рухом?
10. Що необхідно знати для побудови плану швидкостей?
11. Яка існує залежність між прискоренням точки плоскої фігури і прискоренням полюса?
Висновок по темі: Кутова швидкість плоскої фігури визначається діленням швидкостей любої точки цієї фігури на відстань цієї точки до міттевого центру швидкостей.
3. Динаміка
3.1 Динаміка точки
В даній темі при її вивченні необхідно звернути увагу на систему одиниць Розглянути. Диференціальні рівняння руху вільної матеріальної точки
Ознайомитись з основними законами динаміки: законами Ньютона, що покладені в основу динаміки, умовами прямолінійного руху матеріальної точки.
Вивчити першу і другу основні задачі динаміки точки.
|
|
|
Розглянути приклад розв’язання задач динаміки.
Приклад. Кузов трамвайного вагона разом з вантажем P1=100 кH здійснює при русі на ресорах вертикальні коливання по закону  на візку з колесами (рис. 1). Визначити найбільший і найменший тиск вагона на рейки 3 горизонтального прямолінійного відрізку шляху, якщо візок з колесами важить Р2 = 10кН.
на візку з колесами (рис. 1). Визначити найбільший і найменший тиск вагона на рейки 3 горизонтального прямолінійного відрізку шляху, якщо візок з колесами важить Р2 = 10кН.
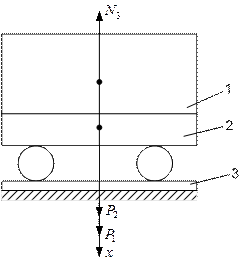 Рис. 1
Рис. 1
| Розв’язання
Розглянемо рух кузова. Рух цей прямолінійний і проходить уздовж осі х. Тому з трьох рівнянь руху використаємо одне, що в даному випадку приймає вигляд
 де
де 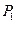 и и 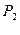 ‑ відомі з умов приклада ваги кузова і візка з колесами, ‑ відомі з умов приклада ваги кузова і візка з колесами,
|
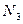 ‑ реактивна сила з боку в’язів, рейки.
‑ реактивна сила з боку в’язів, рейки.
Звідси 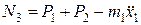 .
.
З умови приклада маємо:
 ‑ закон руху кузова на ресорах.
‑ закон руху кузова на ресорах.
Тоді 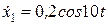 ,
,
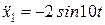 ‑ проекція прискорення кузова в напрямку осі х
‑ проекція прискорення кузова в напрямку осі х
 ;
;
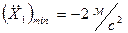 .
.
Звідси 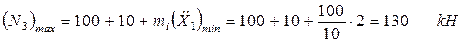 ;
;
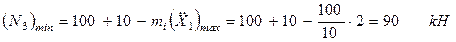 .
.
Відповідь:  .
.
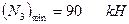
При розгляді даної теми необхідно використовувати посібник: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 217 – 227.
Теоретичні відомості
Динаміка точки
1. Основні закони динаміки.
2. Диференціальні рівняння руху вільної матеріальної точки.
3. Основі задачі динаміки точки.
Література
1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.
2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.
1. Основні закони динаміки.
Динамікою називається розділ теоретичної механіки, в якому визначається механічний рух матеріальної точки, системи матеріальних точок, твердого тіла під дією прикладених до них сил.
Основоположником динаміки є великий італійський вчений Галілей (1564 – 1642). Він вперше ввів у механіку поняття швидкості і прискорення точки при нерівномірному прямолінійному русі і встановив закони падіння тіл у пустоті. Галілей сформулював перший закон динаміки – закон інерції. Почата Галілеєм робота по створенню динаміки була завершена великим англійським вченим І. Ньютоном (1643 – 1727), який формулює основні закони класичної механіки.
Щоб при загальному вивченні динаміки мати можливість відволікатися від впливу розмірів тіл, вводиться поняття матеріальної точки.
Під матеріальною точкою розуміють матеріальне тіло таких малих розмірів, що відмінністю в русі окремих його точок можна знехтувати і положення якого можна визначити координатами його точки.
Введення поняття про матеріальну точку виправдовує проведений в курсах теоретичної механіки поділ динаміки на дві частини: «Динаміка матеріальної точки» і «Динаміка матеріальної системи».
В розділі «Динаміка матеріальної точки», вивчаючі найбільш простий рух тіла, виясняють принципові поняття і закони динаміки.
В розділі «Динаміка матеріальної системи» переходять до вивчення більш складних рухів тіла, а також до вивчення руху системи тіл.
Маса тіла – це величина, яка характеризує інертність тіла.
Інертність – це властивість тіла чинити опір при спробі привести його у стан руху, або змінити швидкість.
Рівномірний і прямолінійний рух точки називається – рухом по інерції.
Перший закон Ньютона (закон інерції)
Будь-яке тіло (точка) перебуває у стані спокою, або рівномірного та прямолінійного руху, поки деяка причина не виведе його з цього стану.
Другий закон Ньютона (основний закон динаміки)
 Сила, що діє на матеріальну точку, надає їй прискорення, яке пропорційне величині сили і має направлення сили.
Сила, що діє на матеріальну точку, надає їй прискорення, яке пропорційне величині сили і має направлення сили.
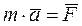
де m – маса матеріальної точки;
а – прискорення матеріальної точки;
F – сила, що діє на точку.
Третій закон Ньютона (закон рівності дії та протидії)
Дії завжди відповідає рівна їй, і протилежно напрямлена протидія, інакше – сили взаємодії двох матеріальних точок завжди між собою рівні і напрямлені в протилежні боки.

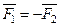
Четвертий закон Ньютона (принцип суперпозиції)
При одночасній дії на матеріальну точку декількох сил, прискорення точки складається з тих прискорень, які були б при роздільній дії сил.

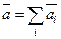
2. Диференційні рівняння руху вільної матеріальної точки.
Диференціальні рівняння руху вільної матеріальної точки отримують шляхом проектування векторного рівняння  на координатні осі:
на координатні осі:
а) В декартовій системі координат:
 ;
; 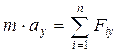 ;
;  ,
,
або  ;
;
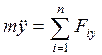 ;
;
 ,
,
де m ‑ маса точки,  - проекції прискорення точки на вісі,
- проекції прискорення точки на вісі,  ‑ алгебраїчні суми проекцій на координатні осі сил, що діють на точку.
‑ алгебраїчні суми проекцій на координатні осі сил, що діють на точку.
Ці рівняння називаються динамічними рівняннями руху матеріальної точки в координатній формі.
Якщо точка рухається в площині, то її рух описується першими двома рівняннями, а якщо по прямій, то тільки одним з них (при цьому вісь слід спрямувати за рухом точки).
б) У природній системі координат в натуральній формі (дотична, нормаль і бінормаль):
 ;
;
 ;
;
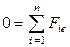 ,
,
де  ‑ проекція швидкості на дотичну
‑ проекція швидкості на дотичну 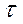 ;
; 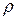 ‑ радіус кривизни траєкторії в даній точці;
‑ радіус кривизни траєкторії в даній точці; 
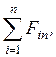
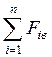 ‑ алгебраїчні суми проекцій всіх сил, які діють на точку, на натуральні осі
‑ алгебраїчні суми проекцій всіх сил, які діють на точку, на натуральні осі 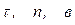 .
.
Ці рівняння називаються динамічними рівняннями руху точки в натуральній формі або у формі Ейлера.
Ця система використовується, якщо рух точки є невільним, коли, завдяки наявності зв¢язків, точка рухається по відомій траєкторії або поверхні.
Перше рівняння є диференціальним, якщо відомі проекції сил на дотичну траєкторії руху. Інші два рівняння дозволяють визначити реакції в¢язів.
Диференціальні рівняння руху матеріальної точки дозволяють вирішити дві основні задачі динаміки.
3. Основі задачі динаміки точки
Перша, або пряма основна задача динаміки: знаючи закон руху точки і її масу, визначити сили, що викликають цей рух.
Якщо рух матеріальної точки масою m задано координатним способом 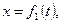

 , то двічі диференціюючи ці співвідношення за часом, одержимо проекції прискорень на координатні осі:
, то двічі диференціюючи ці співвідношення за часом, одержимо проекції прискорень на координатні осі:
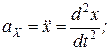
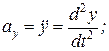
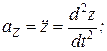 .
.
Використовуючи динамічні рівняння руху матеріальної точки в координатній формі, визначимо проекції сили:
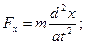
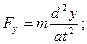

Модуль рівнодійної сили  .
.
Напрям рівнодійної сили визначимо за направленими косинусами

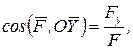
 .
.
Друга, або обернена задача динаміки: визначити кінематичні рівняння руху точки, якщо відомі її маса m, прикладені до неї сили 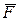 і початкові умови руху. Розв’язання другої задачі динаміки зводиться до інтегрування диференційних рівнянь руху матеріальної точки. Праві частини цих рівнянь відомі. Тому спочатку знаходять проекції сил и F на осі координат (Fx,FyFz), потім інтегрують системи диференційних рівнянь руху матеріальної точки.
і початкові умови руху. Розв’язання другої задачі динаміки зводиться до інтегрування диференційних рівнянь руху матеріальної точки. Праві частини цих рівнянь відомі. Тому спочатку знаходять проекції сил и F на осі координат (Fx,FyFz), потім інтегрують системи диференційних рівнянь руху матеріальної точки.
Загальний розв’язок цієї системи визначає координати точки як функції часу t і шість сталих інтегрування 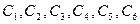 ;
;
 ,
,
 ,
,
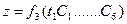 .
.
Сталі інтегрування визначають з початкових умов.
Початкові умови – це шість величин, що визначають положення точки і проекції вектора швидкості в початковий момент часу (t=t 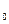 );
);
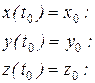
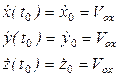
Підставивши знайдені значення сталих інтегрування у загальній розв'язок системи диференційних рівнянь, одержують закон руху точки:
x = x(t); y = y(t); z = z(t).
Отже, розв’язання другої, оберненої задачі динаміки складається з операцій:
1. Складання динамічних рівнянь руху матеріальної точки згідно з умовами задачі.
2. Інтегрування одержаної системи диференційних рівнянь.
3. Визначення значень сталих інтегрування.
4. Знаходження закону руху.
Приклад. Маємо рух матеріальної точки, кинутої під кутом до обрію.
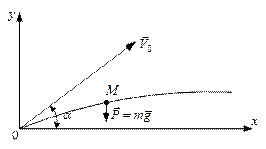 Рис. 8.2
Рис. 8.2
| Визначити рух точки М масою m, яку кинуто з початковою швидкістю V 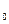 під кутом під кутом 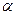 до обрію. Опором повітря знехтувати (рис. 8.2). Визначити траєкторію руху точки. до обрію. Опором повітря знехтувати (рис. 8.2). Визначити траєкторію руху точки.
|
Розв’язання. Початок координат показуємо в початковому положенні точки. Зобразимо рухому матеріальну точку M в довільній точці траєкторії і покажемо діючу на неї силу тяжіння  .
.
У початковий момент часу (t = 0) точка була на початку координат, тому при t=0, x  =0; y
=0; y  =0.
=0.
Проекції початкової швидкості на осі координат:
при  .
.
Щоб визначити залежність координат х, у точки від часу, скористаємося диференційним рівняннями руху точки:
 ,
,
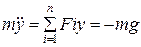 , або після скорочення на m
, або після скорочення на m
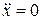 ,
,
 .
.
Інтегруючі ці рівняння, одержимо
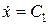 ,
,
 .
.
Сталі інтегрування знайдемо з початкових умов:
при t=0
 ,
,
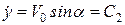 .
.
Отже
 ,
,
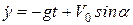 .
.
Звідси після інтегрування одержимо
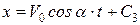 ,
,
 .
.
Сталі інтегрування С  і С
і С 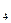 знаходимо з початкових умов руху. При t=0 x
знаходимо з початкових умов руху. При t=0 x 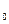 =0; y
=0; y 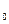 =0, тому С
=0, тому С  =С
=С 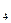 =0
=0
Тоді закон руху точки М матиме вигляд
 ,
,
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 725; Нарушение авторских прав?; Мы поможем в написании вашей работы!