Потужність зчисленних множин

Потужністю зчисленної множини ν називається потужність множини натуральних чисел N. Довільна множина, рівнопотужна N, називається зчисленною. Множина зчисленна, якщо існує хоча б одна бієкція цієї множини в множину N.

Теорема 6. ν - найменше трансфінітне кардинальне число.

Це означає, що довільна нескінченна множина X містить хоча б одну зчисленну підмножину.

Теорема 7. Для довільного скінченого числа т ≥ 1 виконуються рівності т ∙ ν = ν і ν ^т = ν. Результат випливає безпосередньо з теореми 5, згідно з якою т ∙ ν = ν при т ≤ ν і ν ² = ν ∙ ν = ν, а це означає за індукцією ν ^т = ν.

Теорему 4 ми прийняли без доведення. Але рівність ν ² = ν∙ν = ν, з якої випливає теорема 7, можна легко довести. Покажемо, що N ´ N рівнопотужна N. Дійсно зі схеми, наведеної нижче

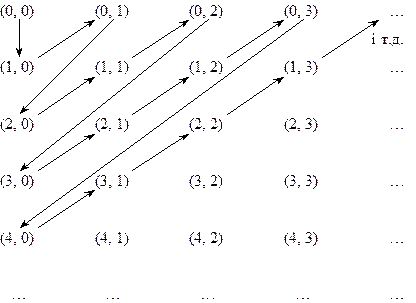
ми бачимо, що відображення 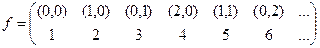, тобто f: N ´ N → N є бієкцією.

На основі викладеного можна зробити такі висновки:

1) об’єднання скінченної або зчисленої множини скінченних чи зчислених підмножин множини X є скінченною або зчисленною множиною. Дійсно, нехай J - деяка підмножна N і підмножини A _j, j Î J деякої множини X всі непорожні. Нехай f _j: N → A _j сюр’єкція. Тоді (j, п) → f _j (n) буде сюр’єкцією J ´ N → . Оскільки J ´ N зчисленна, то скінченна або зчисленна;

2) множина Z всіх цілих чисел зчисленна (як об’єднання двох зчисленних множин). Множина Q раціональних чисел зчисленна. Дійсно відображення, яке ставить кожній парі (p, q), q ≠ 0 множини Z ´ Z у відповідність раціональне число p / q, є сюр’єкцією підмножини Z ´ Z на Q. Це означає, що Q не більш, ніж зчисленна, але так як вона містить N, то Q зчисленна;

3) множина алгебраїчних дійсних чисел зчислена. Алгебраїчним дійсним числом називають дійсний корінь деякого тотожньо не рівного нулю полінома з цілими коефіцієнтами. Оскільки тотожньо не рівний нулю поліном степеня ≤ m з цілими коефіцієнтами має т + 1 коефіцієнтів, які є довільними цілими числами і не всі дорівнюють нулю, то потужність множини цих поліномів дорівнює ν ^{т + 1} = ν. Кожен такий поліном має не більше т алгебраїчних дійсних коренів, а значить, множину коренів поліномів степені ≤ т можна розглядати як об’єднання зчисленної множини скінченних множин. Така множина не більш ніж зчисленна, а так як вона нескінченна, то вона зчисленна. Так як т приймає всі значення, то множина всіх алгебраїчних чисел отримується як об’єднання зчисленного числа зчисленних множин, а значить є зчисленною множиною;

4) множина всіх точок простору R ⁿ з раціональними чи алгебраїчними координатами зчисленна, так як її кардинальне число дорівнює ν ^п = ν.

Дата добавления: 2014-11-29