
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритми побудови моделей
|
|
|
|
Модель лінійної регресії (лінійне рівняння) є найпоширенішим видом залежності між економічними змінними.
Скористаймося методом найменших квадратів, суть якого полягає у наступному: сума квадратів відхилень ординат точки, що спостерігається
(Xi, Yi) від відповідної ординати точки, що лежить на регресійній прямій, повинна бути найменшою
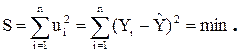 |
Використання 1МНК для оцінки теоретичних параметрів моделі парної регресії приводить до таких систем нормальних рівнянь:
a) лінійна залежність Y = a0 + a1X.
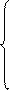
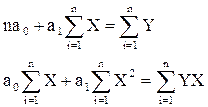
Побудоване лінійне рівняння може слугувати початковою точкою в разі складних (суттєво нелінійних) залежностей.
Нелінійні зв'язки, як правило, певними перетвореннями (заміною змінних чи логарифмуванням) зводять до лінійного вигляду або апроксимують (наближують) лінійними функціями.
б) гіперболічна залежність 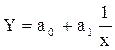 . Замінюємо
. Замінюємо  і отримаємо лінійну модель Y = a0 + a1х′.
і отримаємо лінійну модель Y = a0 + a1х′.
Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

в) параболічна залежність Y = a0 + a1х2. Замінюємо х2 = х′ і отримаємо лінійну модель Y = a0 + a1х′.
Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:
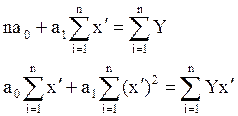
г) степенева залежність  .
.
Логарифмуємо функцію lnY = ln a0 + a1 · ln Х.
Замінюємо логарифми lnY = Y′, ln Х = Х′, ln a0 = a′.
Одержуємо лінійну модель Y′ = a′+ a1 · Х′.
Складаємо систему нормальних рівнянь:
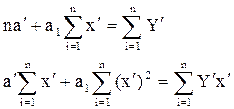
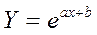 д) експоненціальна.
д) експоненціальна.
Для оцінки теоретичних параметрів зводимо модель до лінійного вигляду:
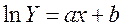 |
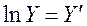 Логарифмуємо функцію
Логарифмуємо функцію
 Замінюємо логарифм
Замінюємо логарифм
Одержуємо лінійну модель
е) проста модифікована експоненціальна 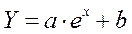
Методом заміни зводимо модель до лінійного вигляду:
|
|
|
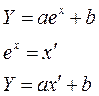
Моделювання здійснюється на основі вибірки статистичних даних, яку студент отримує з відповідних таблиць.
Лабораторні роботи № 1, 2, 3, 4, 5 студент виконує згідно з завданням та варіантом вихідних даних, який отримує у викладача.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 776; Нарушение авторских прав?; Мы поможем в написании вашей работы!