Прогнозування за моделями простої лінійної регресії

Знаходження інтервалів довіри для параметрів а0 і а1 за t- розподілом Стьюдента.

Узагальнена регресійна модель.

План

Тема 2. Методи побудови загальної лінійної моделі

Лекція 3. Імовірнісний зміст простої регресії

2. Критерій Стьюдента для перевірки на значущість параметрів â₀ і â₁ знайдених за методом найменших квадратів.

5. Оператор оцінювання методу найменших квадратів.

1. Економетрична модель – це функція чи система функцій, що описує кореляційно-регресійний зв’язок між економічними показниками, один чи кілька з них є залежною змінною, інші – незалежні.

Незалежні змінні моделі називаються пояснюючими, наперед заданими змінними. Залежні змінні називаються пояснюваними змінними.

Побудова будь-якої економетричної моделі здійснюється як послідовність певних кроків.

Крок 1. Знайомство з економічною теорією, висунення гіпотези взаємозв’язку. Чітка постановка задачі.

Крок 2. Специфікація моделі.

Специфікація моделі – це аналітична форма економетричної моделі. На основі досліджуваних чинників вона складається з певного виду функції чи функцій, що використовуються для побудови моделей, має імовірнісні характеристики, які притаманні стохастичним залишкам моделі.

Крок 3. Формування масивів вхідної інформації згідно з метою та завданнями дослідження.

Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів. Аналіз залишків дає змогу перевірити чи не суперечить специфікація моделі передумовам “класичної” лінійної регресії.

Крок 5. Якщо деякі передумови моделі не виконуються, то для продовження аналізу треба замінити специфікацію або застосувати інші методи оцінювання параметрів.

Крок 6. Проведення аналізу достовірності моделі та прогнозу за побудованою моделлю.

Нехай економетрична модель у матричній формі має вигляд

Y = XA + u,

де Y – вектор значень залежної змінної; X – матриця незалежних змінних розміром n×m (n – число спостережень; m – кількість незалежних змінних); A – вектор параметрів моделі; u – вектор залишків. Залишки моделі обчислюють як різниці між фактичними значеннями залежної змінної та обчисленими за моделлю.

Розглянемо передумови використання методу найменших квадратів:

1) математичне сподівання залишків дорівнює нулю, тобто

M(u) = 0;

2) значення u_і вектора залишків u незалежні між собою і мають постійну дисперсію, тобто

M(uú)= 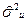E,

де E – одинична матриця;

3) незалежні змінні не пов’язані із залишками:

M(x́u)=0;

4) незалежні змінні моделі утворюють лінійно незалежну систему векторів, або іншими словами незалежні змінні не повинні бути мультиколінеарними.

2. Перевірку гіпотези про значущість параметрів економетричної моделі можна виконати згідно з t- критерієм:

t_j= .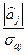

Обчислене значення t- критерію порівнюється з табличним для вибраного рівня довіри і n-m ступенів вільності. Якщо t_факт> t_табл, то відповідний параметр економетричної моделі є достовірним.

Дисперсії параметрів економетричної моделі можна визначити за формулами:

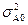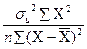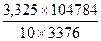= = =117,62, = 10,85;

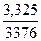= = = 000098, = 0, 031.

Отже, перевіримо гіпотези про значущість оцінок параметрів моделі побудованої на основі вихідних даних, наведених у табл.. 1

t₁= 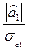= =16,13;

t₀= 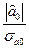= =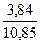0,35.

Якщо ступінь вільності n-m =10-2=8 і рівень значущості α=0,05 t_табл=2,306. Оскільки t_1факт> t_табл , то параметр â₁є значущим, t_0факт < t_табл, то параметр â₀ є незначущим.

Для подальшого аналізу побудованої економетричної моделі визначимо коефіцієнт детермінації. Він показує на скільки відсотків варіація залежної змінної визначається варіацією незалежної змінної.

Перевірити на значущість коефіцієнт детермінації можна за допомогою F-критерію:

F_k-1,n-k= : .

Фактичне значення F-критерію порівнюється з табличним при ступенях вільності k-1 і n-k і при вибраному рівні значущості. Якщо F_факт > F_табл, то гіпотеза про значущість коефіцієнта детермінації підтверджується, у противному разі – відкидається. У нашому випадку:

F_k-1,n-k= : = F_2-1,10-2= : 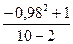=194,02.

Табличне значення F-критерію при ступенях вільності 1 і 8 і рівні значущості 0,95 (F_1,8(0,95)) дорівнює 5,32. Оскільки F_факт >F_табл, то можна зробити висновок про значущість коефіцієнта детермінації.

Перевірити модель на адекватність можна за допомогою також F-критерію:

F_k-1,n-k= .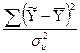

За даними табл. 1 фактичне значення критерію Фішера буде дорівнювати:

F_1,8= 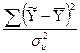= = 238,9.

Оскільки F_факт >F_табл, можна зробити висновок, що побудована модель адекватна реальній дійсності.

Одним із важливих завдань економетричного моделювання є оцінка прогнозного значення залежної змінної за умови, що пояснювальна змінна задана на перспективу. На основі побудованої економетричної моделі можна отримати точковий прогноз залежної змінної на перспективу. Нехай x_прогн=130, тоді y_прогн=3,8 + 0,5 x_прогн= 3,8 + 0,5 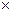130=68,8.

Дата добавления: 2014-12-07