Понятие системы счисления

Системы счисления. Двоичная система. (Лекция 3)

Числа записываются с помощью цифр, а вернее с помощью каких-либо символов. Под системой счисления понимается способ изображения чисел с помощью символов совместно с правилами выполнения действий над этими числами.

Классификация систем счисления.

Все системы делятся на позиционные и непозиционные.

В непозиционных системах каждая цифра имеет свой вес и ее значение не зависит от положения в числе — от позиции. Пример — римская система. Скажем, число 76 в этой системе выглядит так:

LXXVI, где L=50, X=10, V=5, I=1.

Как видно цифрами здесь служат латинские символы.

В позиционных системах значения цифр зависят от их положения (позиции) в числе.

Так, например, человек привык пользоваться десятичной позиционной системой — числа записываются с помощью 10 цифр. Самая правая цифра обозначает единицы, левее — десятки, ещё левее — сотни и т.д.

В любой позиционной системе число может быть представлено в виде многочлена.

Покажем, как представляют в виде многочлена десятичное число.

,

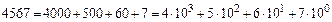а теперь с дробью

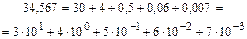
Обобщим это представление на случай использования другого набора цифр.

Основаниемсистемы счисления называется количество цифр и символов, применяющихся для изображения числа. Например р=10.

База системы — это последовательность цифр, используемых для записи числа. Ни в одной системе нет цифры, равной основанию системы.

В настоящее время арифметические действия выполняются в десятичной системе, где р=10.

База этой системы 0,1,2,3,4,5,6,7,8,9,0.

При обработке информации используется восьмеричная и шестнадцатеричная системы, которые применяются для сокращения длины записи при кодировании программы и плотного размещения данных в памяти машины.

Установлено, что, чем больше основание СС, тем компактнее запись числа. Так двоичное изображение числа требует примерно в 3,3 раза больше­го количества цифр, чем его десятичное представление. Рассмотрим два чис­ла: 97D = 1100001В. Двоичное представление числа имеет заметно большее количество цифр.

Несмотря на то что десятичная СС имеет широкое распространение, цифровые ЭВМ строятся на двоичных (цифровых) элементах, так как реали­зовать элементы с десятью четко различимыми состояниями сложно. В другой системе счисления могут работать приборы декатрон и трохотрон. Декатрон — газоразрядная счетная лампа — многоэлектродный газоразрядный прибор тлеющего разряда для индикации числа импульсов в десятичной СС.

Указанные устройства не нашли применения для построения средств ВТ. Историческое развитие вычислительной техники сложилось таким обра­зом, что цифровые ЭВМ строятся на базе двоичных цифровых устройств (триггеров, регистров, счетчиков, логических элементов и т. п.).

Шестнадцатеричная и восьмеричная СС используются при составле­нии программ на языке машинных кодов для более короткой и удобной за­писи двоичных кодов— команд, данных, адресов и операндов. Перевод из двоичной СС в шестнадцатеричную и восьмеричную СС (и обратно) осуще­ствляется достаточно просто.

Задача перевода из одной системы счисления в другую часто встреча­ется при программировании и особенно часто при программировании на языке Ассемблера. Например, при определении адреса ячейки памяти, для получения двоичного или шестнадцатеричного эквивалента десятичного числа. Отдельные стандартные процедуры языков программирования Пас­каль, Бейсик, HTML и Си требуют задания параметров в шестнадцатеричной системе счисления. Для непосредственного редактирования данных, запи­санных на жесткий диск, также необходимо умение работать с шестнадцатеричными числами. Отыскать неисправность в ЭВМ практически невозможно без представлений о двоичной системе счисления.Без двоичной СС невоз­можно понять принципы криптографии и стеганографии.

Дата добавления: 2014-12-07