Понятие вероятности. Средние значения случайных величин

1. Большинство физических величин изменяется хаотически, т.е. являются случайными величинами. Различают дискретные и непрерывные случайные величины. Дискретная величина принимает строго определенный ряд значений , в интервалах между которыми не может принять ни одного значения. Непрерывная величина может принимать любые сколь угодно близкие друг к другу значения на промежутке .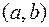

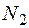Пусть произведено измерений дискретной случайной величины, при этом раз получилось значение 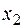, раз получилось значение , …, раз получилось значение 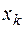. Величина называется относительной частотой появления при измерении значения (относительной частотой случайного события с номером . При этом и 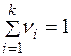. В пределе при очень большом числе измерений, относительная частота появления случайного события называется вероятностью этого события

.

Сумма вероятностей всех возможных событий равна единице

.

Это условие называется условием нормировки вероятности.

2. Среднее значение случайной величины при измерениях

в пределе при принимает вид

. (1)

Данное соотношение позволяет рассчитывать среднее значение дискретной случайной величины, если известен закон распределения вероятности по возможным значениям случайной величины.

Пусть, например, случайная величина принимает дискретный ряд значений 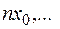, и пусть закон распределения имеет вид

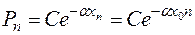. (2)

Из условия нормировки вероятности

находим нормировочную постоянную

.

В соответствии с формулой (1) для среднего значения запишем выражение

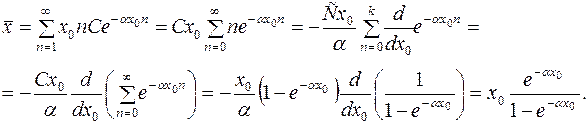
Таким образом, в рассмотренном примере среднее значение вычисляется по формуле

(3)

3. Обратимся теперь к непрерывной случайной величине.

Для непрерывной случайной величины, определенной на промежутке существует бесконечное множество значений. Поэтому для непрерывной случайной величины говорить о вероятности конкретного значения бессмысленно. При измерении очень многие значения просто не выпадут. Для таких величин рассматривают вероятность того, что при измерении получится значение в интервале от 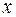до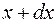

.

Здесь полное число измерений, - число измерений в которых значение случайной величины попало в интервал от 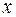до 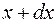, а величина

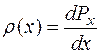
называется плотностью вероятности (вероятность, приходящаяся на единичный интервал значений случайной величины). Она и описывает закон распределения вероятности по значениям случайной величины. Условие нормировки вероятности в этом случае имеет вид

.

Среднее значение для непрерывной случайной величины по аналогии с дискретной величиной рассчитывается по формуле

. (4)

Пусть, например, случайная величина принимает непрерывный ряд значений в интервале 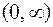, и пусть закон распределения имеет вид

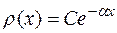. (5)

Из условия нормировки вероятности

находим нормировочную постоянную

.

В соответствии с формулой (3) для среднего значения запишем выражение

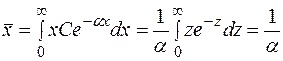. (6)

Сравнение формул (3) и (6) показывает, что при одинаковом экспоненциальном законе распределения вероятности средние значения для дискретной и непрерывной величин отличаются существенно, особенно при , но при можно воспользоваться приближенным выражением для экспоненты 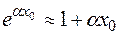. В этом случае формула (3) переходит в формулу (6).

Дата добавления: 2014-11-29