
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аналитический метод. № 5. Решить симплексным методом задачу линейного программирования:
|
|
|
|
№ 5. Решить симплексным методом задачу линейного программирования:
Найти
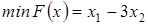 ,
,
при ограничениях:
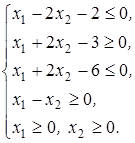
Решение. Приведем эту ЗЛП к каноническому виду, для чего введем дополнительные переменные:  ,
, 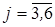 :
:
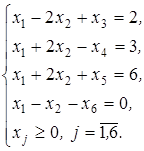
Так как определитель, составленный из коэффициентов при дополнительных переменных, не равен нулю, то эти переменные и возьмем в качестве основных.
1 шаг. Основные переменные 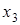 ,
, 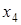 ,
, 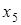 ,
, 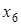 ; свободные -
; свободные - 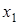 и
и 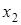 . Выразим основные переменные через свободные:
. Выразим основные переменные через свободные:


Положив свободные переменные равными нулю 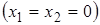 , получим базисное решение:
, получим базисное решение:
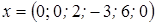 .
.
Оно не является допустимым, так как 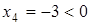 . Следовательно, надо перевести или
. Следовательно, надо перевести или 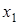 , или
, или 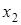 в основные, то есть увеличить.
в основные, то есть увеличить.
Допустимую границу увеличения значений свободных переменных определяем как наименьшее из отношений свободных членов 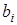 к коэффициенту при соответствующей свободной переменной
к коэффициенту при соответствующей свободной переменной 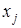 по абсолютной величине. При этом придерживаются следующих правил:
по абсолютной величине. При этом придерживаются следующих правил:
1) 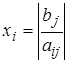 , если
, если 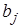 и
и 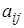 имеют разные знаки;
имеют разные знаки;
2) 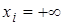 , если
, если 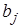 и
и 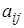 имеют одинаковые знаки;
имеют одинаковые знаки;
3) 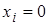 , если
, если 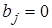 и
и  ;
;
4) 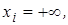 если
если 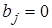 и
и  ;
;
5) 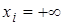 , если
, если 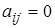 .
.
Тогда:
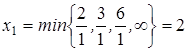 .
.
Символ «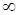 » означает здесь, что в четвертом уравнении
» означает здесь, что в четвертом уравнении 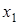 можно увеличить до бесконечности, при этом будет
можно увеличить до бесконечности, при этом будет  . Для
. Для 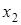 имеем:
имеем:
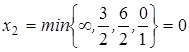 .
.
Здесь «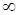 » означает, что свободный член и коэффициент (2) при
» означает, что свободный член и коэффициент (2) при 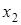 в первом уравнении имеют одинаковые знаки.
в первом уравнении имеют одинаковые знаки.
Так как 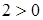 , то переведем в основные
, то переведем в основные 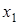 . При этом в свободные переходит переменная
. При этом в свободные переходит переменная 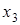 .
.
2 шаг. Основные переменные - 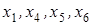 , свободные -
, свободные - 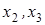 . Выразим основные переменные через свободные:
. Выразим основные переменные через свободные:
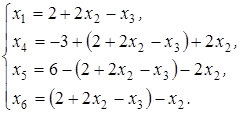
или

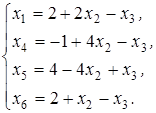
Положив 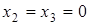 , получим базисное решение:
, получим базисное решение:
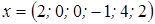 .
.
Оно снова не является допустимым, так как 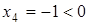 . Поэтому надо перевести в основные переменную
. Поэтому надо перевести в основные переменную 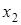 по правилу:
по правилу:
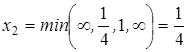 .
.
При этом в свободные перейдет переменная 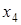 .
.
3 шаг. Основные переменные - 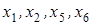 , свободные -
, свободные - 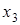 и
и 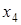 . Выразим основные переменные через свободные:
. Выразим основные переменные через свободные:

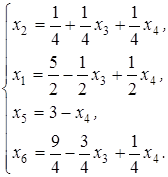
Найдем базисное решение:
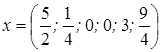 .
.
Оно оказалось допустимым, поэтому найдем значение целевой функции:
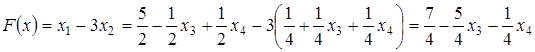 ,
,
а именно:
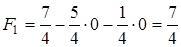 .
.
Это допустимое базисное решение не является оптимальным, так как и 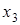 и
и 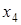 входят в целевую функцию с отрицательными коэффициентами. Поэтому значение целевой функции можно уменьшить за счет увеличения значений свободных переменных. Для определенности переведем в основные переменную
входят в целевую функцию с отрицательными коэффициентами. Поэтому значение целевой функции можно уменьшить за счет увеличения значений свободных переменных. Для определенности переведем в основные переменную 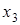 , так как
, так как 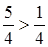 .
.
Вычислив
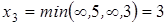 ,
,
переведем в свободные переменную 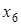 .
.
4 шаг. Основные переменные - 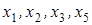 , свободные -
, свободные - 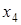 и
и 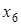 . Тогда:
. Тогда:

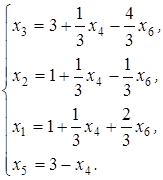
и целевая функция примет вид:
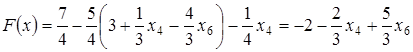 .
.
Вычислим значение целевой функции при базисном решении:
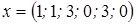 ,
,
а именно
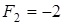 .
.
Видно, что действительно 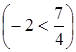 значение целевой функции улучшается (уменьшается).
значение целевой функции улучшается (уменьшается).
Это допустимое решение также не является оптимальным, так как значение целевой функции можно улучшить за счет переменной 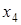 , имеющей отрицательный коэффициент
, имеющей отрицательный коэффициент 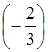 .
.
Вычислив
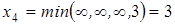 ,
,
переведем 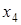 в основные, а
в основные, а 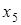 в свободные.
в свободные.
5 шаг. Основные переменные - 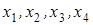 , свободные -
, свободные - 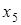 и
и 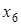 . Тогда
. Тогда
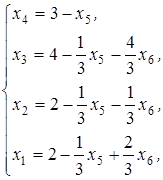
с целевой функцией:
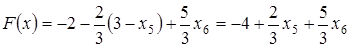 ,
,
и базисным решением
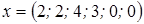 .
.
Так как все коэффициенты при переменных в 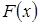 положительны, то невозможно уменьшить далее значение целевой функции. Следовательно,
положительны, то невозможно уменьшить далее значение целевой функции. Следовательно,
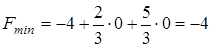 ,
,
и оптимальное решение:

Ответ: 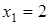 ,
, 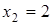 ,
, 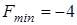 .
.
Для определения максимума линейной функции 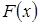 на каждом шаге увеличивают целевую функцию за счет той свободной переменной, которая входит в
на каждом шаге увеличивают целевую функцию за счет той свободной переменной, которая входит в 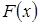 с положительным коэффициентом. И решение будет оптимальным, если все коэффициенты при переменных в целевой функции будут отрицательными.
с положительным коэффициентом. И решение будет оптимальным, если все коэффициенты при переменных в целевой функции будут отрицательными.
№ 6. В условиях №5 решить задачу на максимум.
Решение. На третьем шаге была найдена целевая функция:
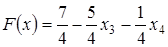 .
.
Так как все коэффициенты при свободных переменных отрицательны, то дальнейшее увеличение значений целевой функции невозможно. Следовательно
 ,
,
и
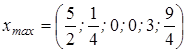 ,
,
а именно,
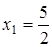 ,
, 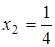 .
.
Ответ: 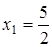 ;
; 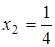 ;
;  .
.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 412; Нарушение авторских прав?; Мы поможем в написании вашей работы!