Решение систем линейных алгебраических уравнений

Цель работы: Изучение возможностей пакета Ms Excel при решении задач линейной алгебры. Приобретение навыков решения систем линейных алгебраических уравнений.

Задание: Решить систему линейных уравнений:

a) Методом обратной матрицы (на листе 1);

b) Методом Крамера (на листе 2).

Таблица 4.1

Варианты задания

Продолжение табл. 4.1.

Продолжение табл. 4.1.

Порядок выполнения задания

При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.

Метод обратной матрицы.

Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к А. Система уравнений примет вид:

A^-1*AX=A^-1* b, EX=A^-1* b, (E - единичная матрица).

Таким образом, вектор неизвестных вычисляется по формуле X=A^-1*b.

Метод Крамера.

В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:

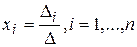
где Δ – определитель матрицы A;

Δ _i –определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.

Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.

Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на конкретных примерах. Решим следующую систему линейных алгебраических уравнений методом обратной матрицы:

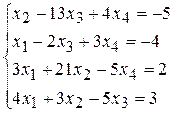
В этом случае матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:

Введём матрицу A и вектор b в рабочий лист MS Excel (рис. 4.1).

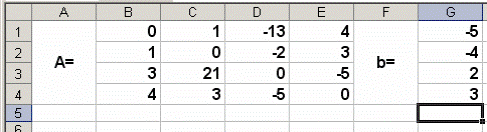
Рис. 4.1. Ввод матрицы A и вектора b

В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1: Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно!!!); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории «Математические» выберем функцию МОБР, предназначенную для вычисления обратной матрицы (рис. 4.2), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода «Массив» (рис. 4.3).

Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица – в нашем случае B1:E4. Данные в поле ввода «Массив» можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.

Рис. 4.2. Мастер функций

Рис. 4.3. Нахождение обратной матрицы

Если поле «Массив» заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид, изображенный на рис. 4.4.

Рис. 4.4. Фрагмент рабочего листа с полученной обратной матрицей Aобр

Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА

Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно (рис. 4.5) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b)

Рис. 4.5. Перемножение обратной матрицы Aобр и вектора В

Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений (вектор X), находится в ячейках G6:G9 (рис. 4.6).

Рис. 4.6. Фрагмент рабочего листа с найденным вектором X

Таким образом, мы решили систему линейных алгебраических уравнений методом обратной матрицы. Корни: X1, X2, X3, X4 будут, в нашем случае, соответствовать ячейкам G6, G7, G8 и G9.

Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор Х и получить в результате вектор b. Умножение матрицы A на вектор Х осуществляется при помощи функции МУМНОЖ(В1:Е4;G6:G9) так, как было описано выше. В результате проведенных вычислений рабочий лист примет вид, изображенный на рис. 4.7.

Рис. 4.7. Фрагмент рабочего листа с результатом проверки решения

Теперь рассмотрим пример решения этой же системы линейных алгебраических уравнений методом Крамера. Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 4.8)

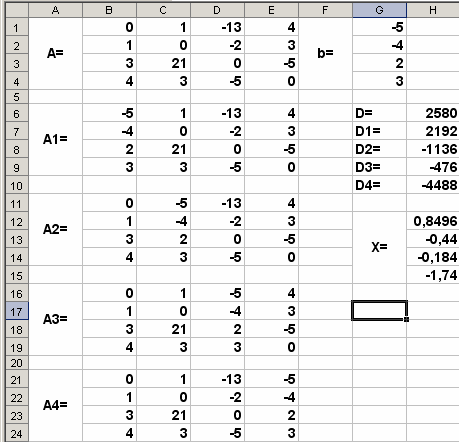
Рис. 4.8. Фрагмент рабочего листа с результатом решения системы методом Крамера

Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку H6 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге, содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.

Для вычисления вспомогательных определителей введем формулы:

H7=МОПРЕД(B6:E9),

H8=МОПРЕД(B11:E14),

H9=МОПРЕД(B16:E19),

H10=МОПРЕД(B21:E24).

В результате в ячейке H6 хранится главный определитель, а в ячейках

H7:H10 – вспомогательные.

Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку H12 введём формулу =H7/$H$6. Затем скопируем её содержимое в ячейки H13, H14 и H15. Система решена.

Дата добавления: 2014-12-27