Матричные игры. Игры с природой

В процессе целенаправленной человеческой деятельности возникают ситуации, в которых интересы отдельных лиц (участников, групп, сторон) либо прямо противоположны (антагонистичны), либо, не будучи непримиримыми, все же не совпадают. Простейшими и наиболее наглядными примерами таких ситуаций являются спортивные игры, арбитражные спо­ры, военные учения (маневры), борьба между блоками избирателей за своих кандидатов, в международных отношениях - отстаивание интересов своего государства и т. п. Здесь каж­дый из участников сознательно стремится добиться наилучшего результата за счет другого участника. Подобного рода ситуации встречаются и в различных сферах производствен­ной деятельности.

Все ситуации, когда эффективность действия одного из участников зависит от действий других, можно разбить на два типа: интересы участников совпадают, и они могут договориться о совместных действиях; интересы участников не совпадают. В этих случаях может оказаться невыгодным сообщать другим участникам свои решения, так как кто-нибудь из них сможет воспользоваться знанием чужих решений и получит больший выигрыш за счет других участников. Ситуации такого типа называются конфликтными.

Для указанных ситуаций характерно, что эффективность решений, принимаемых в ходе конфликта каждой из сторон, существенно зависит от действий другой стороны. При этом ни одна из сторон не мо­жет полностью контролировать положение, так как и той и другой стороне решения приходится принимать в условиях неопределенности. Так, при определении объема выпуска про­дукции на одном предприятии нельзя не учитывать размеров выпуска аналогичной продукции на других предприятиях. В реальных условиях нередко возникают ситуации, в которых антагонизм отсутствует, но существуют противоположные тен­денции. Например, для нормального функционирования про­изводства, с одной стороны, необходимо наличие запасов разно­образных ресурсов, но с другой - стремление к чрезвычайному увеличению этих запасов вызывает дополнительные затраты по их содержанию и хранению. В приведенных примерах кон­фликтные ситуации возникают в результате сознательной де­ятельности людей. Однако на практике встречаются неопределенности, которые порождаются не сознательным противо­действием другой стороны, а недостаточной информированно­стью об условиях проведения планируемой операции.

Раздел математики, изучающий конфликтные ситуации на основе их математических моделей, называется теорией игр. Таким образом, теория игр - это математическая теория кон­фликтных ситуаций, разрабатывающая рекомендации по наи­более рациональному образу действий каждого из участников в ходе конфликтной ситуации, т. е. таких действий, которые обеспечивали бы ему наилучший результат. Игровую схему можно придать многим ситуациям в экономике. Здесь выиг­рышем могут быть эффективность использования дефицит­ных ресурсов, производственных фондов, величина прибыли, себестоимость и т. д.

Необходимо подчеркнуть, что методы и рекомендации тео­рии игр разрабатываются применительно к таким специфи­ческим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то реко­мендации теории игр теряют смысл.

Чтобы проанализировать конфликтную ситуацию по ее математической модели, ситуацию необходимо упростить, учтя лишь важнейшие факторы, существенно влияющие на ход конфликта.

Определение 1. Игрой называется упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилам.

Игра - это совокупность правил, оп­ределяющих возможные действия (чистые стратегии) участ­ников игры. Суть игры в том, что каждый из участников при­нимает такие решения в развивающейся конфликтной ситуа­ции, которые, как он полагает, могут обеспечить ему наилуч­ший исход. Исход игры - это значение некоторой функции, называемой функцией выигрыша (платежной функцией), ко­торая может задаваться либо аналитически выражением, либо таблично (матрицей). В дальнейшем будем рассматривать только такие игры, в которых выигрыш выражается количе­ственно: стоимостью, баллами и т. д.

Величина выигрыша зависит от стратегии, применяемой игроком.

Определение 2. Стратегией игрока называется совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры.

Определение 3. Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш.

Основное предположение, исходя из которого находят оптимальные стратегии, состоит в том, что противник по меньшей мере так же разумен, как и сам игрок, и делает все для того, чтобы добиться своей цели.

Количество стратегий у каждого игрока может быть конечным или бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные.

Вся­кая игра состоит из отдельных партий.

Определение 4. Партией называется каждый вариант реализации игры определенным образом.

В свою очередь, в партии игроки совершают конкретные ходы.

Определение 5. Ходом называется выбор и реализация игроком одного из допустимых вариантов поведения.

Ходы бывают личные и случайные. При личном ходе игрок самостоятельно и осознанно выбирает и реализует ту или иную чистую стратегию. Например, в шахматах каждый ход является личным. При случайном ходе выбор чистой стратегии производится с использованием како­го-либо механизма случайного выбора, например с применени­ем таблицы случайных чисел.

Конфликтные ситуации, встречающиеся в практике, порож­дают различные виды игр. Классифицировать игры можно по разным признакам. Различают, например, игры по количеству игроков. В игре может участвовать любое конечное число иг­роков.

Определение 6. Если в игре игроки объединяются в две группы, преследующие противоположные цели, то такая игра называется игрой двух лиц (парная игра).

В зависимости от количества стратегий в игре они делятся на конечные или бесконеч­ные. В зависимости от взаимоотношений участников разли­чают игры бескоалиционные (участники не имеют права заключать соглашения), или некооперативные, и коали­ционные, или кооперативные. По характеру выигрышей игры делятся на игры с нулевой суммой и ненулевой суммой.

Определение 7. Игрой с нулевой суммой называется игра, в которой общий капитал игроков не меняется, а лишь перераспределяется в ходе игры, в связи с чем сумма выигрышей равна нулю (проигрыш принимается как отрицательный выигрыш).

В играх с ненулевой суммой сумма выиг­рышей отлична от нуля. Например, при проведении лотереи часть взноса участников идет организатору лотереи.

По виду функции выигрыша игры делятся на матричные, биматричные, непрерывные, выпуклые, сепарабельные и др.

Определение 8. Матричной игрой (при двух участниках) называется игра, в которой выигрыши первого игрока (проигрыши второго игрока) задаются матрицей.

В биматричных играх выигрыши каждого игрока задаются своей матрицей. Другие типы таких игр различаются видом аналитического выражения платежной функции. По количеству ходов игры делятся на одноходовые (выигрыш распределяется после одного хода каждого игрока) и многоходовые (выигрыш распределяется после нескольких ходов). Многоходовые игры в свою очередь делятся на позиционные, стохастические, дифференциальные и др. В зависимости от объема имеющейся информации различают игры с полной и неполной информацией.

В реальных конфликтных ситуациях каждый из игроков сознательно стремится найти наилучшее для себя поведение, имея общее представление о множестве допустимых для партнера ответных действий, но не ведая о том, какое же конкретное решение будет выбрано им в данный момент. В этом проявляется в равной мере неопределен­ность ситуации для каждого из партнеров.

Определение 9. Игры, в которых участники стремятся добиться для себя наилучшего результа­та, сознательно выбирая допустимые правилами игры способы действий, называются стратегическими.

Однако в экономической практике нередко приходится формализовать (мо­делировать) ситуации, придавая им игровую схему, в которых один из участников безразличен к результату игры. Такие игры называют играми с природой, понимая под термином "природа" всю совокупность внешних обстоятельств, в которых сознательному игроку (его называют иногда статистиком, а со­ответствующую игру - статистической) приходится принимать решение. Например, выбор агрономической службой сельско­хозяйственного предприятия участков для посева той или иной культуры в надежде получить в предстоящем году наилуч­ший урожай; определение объема выпуска сезонной продук­ции в ожидании наиболее выгодного для ее реализации уров­ня спроса; формирование пакета ценных бумаг в расчете на высокие дивиденды и т. п. Здесь в качестве второго игрока выступает: в первом примере - в буквальном смысле приро­да; во втором - уровень спроса; в третьем - размеры ожидае­мой прибыли.

В играх с природой степень неопределенности для созна­тельного игрока (статистика) возрастает: если в стратегичес­ких играх каждый из участников постоянно ожидает наихуд­шего для себя ответного действия партнера, то в статистичес­ких играх "природа", будучи индифферентной в отношении вы­игрыша инстанцией, может предпринимать и такие ответные действия (будем говорить: реализовывать такие состояния), ко­торые ей совершенно невыгодны, а выгодны сознательному игроку (статистику).

В дальнейшем мы будем рассматривать только парные матричные игры с нулевой суммой.

Решение матричной игры в чистых стратегиях

Рассмотрим простейшую математическую модель конечной конфликтной ситуации, в которой имеется два участника и выигрыш одного равен проигрышу другого. Такая модель называется антагонистической игрой двух лиц с нулевой суммой. Игра состоит из двух ходов: игрок А выбирает одну из возможных стратегий А_i, , а игрок В выбирает одну из возможных стратегий В_j, . Каждый выбор производится при полном незнании выбора соперника. В результате выигрыш игроков составит соответственно a_ij и - a_ij. Цель игрока А - максимизировать величину a_ij, а игрока В - минимизировать эту величину.

Определение 1. Матрица, составленная из величин a_ij, , ,

называется платежной матрицей, или матрицей игры. Каждый элемент платежной матрицы a_ij, , равен выигрышу А (проигрышу В), если он выбрал стратегию А_i, , а игрок В выбирал стратегию В_j, .

Пример. В игре участвуют первый и второй игроки, каждый из них может записать независимо от другого цифры 1, 2 и 3. Если разность между цифрами, записанная игроками, положительна, то первый игрок выигрывает количество очков, равное разности между цифрами, и, наоборот, если разность отрицательна, то выигрывает второй игрок. Если разность равна нулю, то игра заканчивается вничью.

У первого игрока три стратегии (варианта действия): А ₁ (записать 1), А ₂ (записать 2), А ₃ (записать 3); у второго игрока также три стратегии: В ₁, В ₂, В ₃ (см. таблицу).

	В 1 = 1	В 2 = 2	В 3 = 3
А 1 = 1		-1	-2
А 2 = 2			-1
А 3 = 3

Задача первого игрока - максимизировать свой выигрыш. Задача второго игрока - минимизировать свой проигрыш или минимизировать выигрыш первого игрока. Платежная матрица имеет вид

.

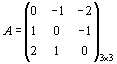Задача каждого из игроков - найти наилучшую стратегию игры, при этом предполагается, что противники одинаково разумны и каждый из них делает все, чтобы получить наибольший доход.

Найдем наилучшую стратегию первого игрока. Если игрок А выбрал стратегию А_i, , то в худшем случае (например, если его ход известен В) он получит выигрыш 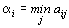. Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш.

.

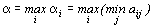Определение 2. Величина a - гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия A_iопт, обеспечивающая получение выигрыша a, называется максиминной.

Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше a.

Аналогично определяется наилучшая стратегия второго игрока. Игрок В при выборе стратегии В _j, в худшем случае получит проигрыш . Он выбирает стратегию B_jопт, при которой его проигрыш будет минимальным и составит

.

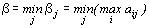Определение 3. Величина b - гарантированный проигрыш игрока В называется верхней ценой игры. Стратегия B_jопт, обеспечивающая получение проигрыша b, называется минимаксной.

Если второй игрок будет придерживаться своей минимаксной стратегии, то у него есть гарантия, что он в любом случае проиграет не больше b.

Фактический выигрыш игрока А (проигрыш игрока В) при разумных действиях партнеров ограничен верхней и нижней ценой игры. Для матричной игры справедливо неравенство a £ b.

Определение 4. Если a = b =v, т. е.

= ,

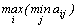то выигрыш игрока А (проигрыш игрока В) оределяется числом v. Оно называется ценой игры.

Определение 5. Если a = b =v, то такая игра называется игрой с седловой точкой, элемент матрицы а_{iопт jопт} = v, соответствующий паре оптимальных стратегий (A_iопт, B_jопт), называется седловой точкой матрицы. Этот элемент является ценой игры.

Седловой точке соответствуют оптимальные стратегии игроков. Их совокупность – решение игры, которое обладает свойством: если один из игроков придерживается оптимальной стратегии, то второму отклонение от своей оптимальной стратегии не может быть выгодным.

Определение 6. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.

Найдем решение игры рассмотренного выше примера:

,

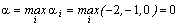a = a ₃ - нижняя цена игры.

,

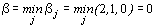b = b ₃ - верхняя цена игры.

Так как a = b = 0, матрица игры имеет седловую точку.

Оптимальная стратегия первого игрока – А₃, второго - B ₃. Из таблицы видно, что отклонение первого игрока от оптимальной стратегии уменьшает его выигрыш, а отклонение второго игрока от В ₃ увеличивает его проигрыш.

Наличие седловой точки в игре – это далеко не правило, скорее, исключение. Существует разновидность игр, которые всегда имеют седловую точку и, значит, решаются в чистых стратегиях. Это так называемые игры с полной информацией.

Определение 7. Игрой с полной информацией называется такая игра, в которой каждый игрок при каждом личном ходе знает всю предысторию ее развития, т.е. результаты всех предыдущих ходов.

Примерами игр с полной информацией могут служить шашки, шахматы, "крестики-нолики" и т.д.

Теорема 1. Каждая игра с полной информацией имеет седловую точку и, значит, имеет решение в чистых стратегиях.

В каждой игре с полной информацией существует пара оптимальных стратегий, дающая устойчивый выигрыш, равный цене игры v. Если решение игры известно, сама игра теряет смысл. Например, шахматная игра либо кончается выигрышем белых, либо выигрышем черных, либо ничьей, только чем именно – мы пока не знаем (к счастью для любителей шахмат). Прибавим еще: вряд ли будем знать в обозримом будущем, так как число стратегий так велико, что крайне трудно привести шахматную игру к матричной форме и найти в ней седловую точку.

Решение матричной игры в смешанных стратегиях

Если платежная матрица не имеет седловой точки, т.е. a <b и , то поиск решения игры приводит к применению сложной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами.

Определение 1. Сложная стратегия, состоящая в случайном применении всех стратегий с определенными частотами, называется смешанной.

В игре, матрица которой имеет размерность m ´ n, стратегии первого игрока задаются наборами вероятностей 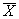(x ₁, x ₂,..., x_m), с которыми игрок применяет свои чистые стратегии. Эти наборы можно рассмотреть как m -мерные векторы, для координат которых выполняются условия

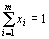, x_i ³ 0, .

Аналогично для второго игрока наборы вероятностей определяют n -мерные векторы (y ₁, y ₂,..., y_n), для координат которых выполняются условия

= 1, y_j ³ 0, .

Выигрыш первого игрока при использовании смешанных стратегий определяют как математическое ожидание выигрыша, т.е. он равен

.

Теорема 1. (Неймана. Основная теорема теории игр.) Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.

Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: a £ v £ b.

Применение первым игроком оптимальной стратегии _опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение

, .

Аналогично для второго игрока оптимальная стратегия _опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение

, .

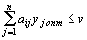Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому матрицы большой размерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и не доминирующих стратегий.

Определение 2. Дублирующими называются стратегии, у которых соответствующие элементы платежной матрицы одинаковы.

Определение 3. Если все элементы i-й строки платежной матрицы больше соответствующих элементов k-й строки, то
i-я стратегия игрока А называется доминирующей над k-й стратегией. Если все элементы j-го столбца платежной матрицы меньше соответствующих элементов k-го столбца, то j-я стратегия игрока В называется доминирующей над k-й стратегией.

Пример. Рассмотрим игру, представленную платежной матрицей

.

a = max (2, 2, 3, 2) = 3, b = min (7, 6, 6, 4, 5) = 4, a ¹ b, .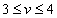

Все элементы стратегии А ₂ меньше элементов стратегии А ₃, т.е. А ₂ заведомо невыгодна для первого игрока и ее можно исключить. Все элементы А ₄ меньше А ₃, исключаем А ₄.

.

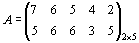Для второго игрока: сравнивая В ₁ и В ₄, исключаем В ₁; сравнивая В ₂ и В ₄, исключаем В ₂; сравнивая В ₃ и В ₄, исключаем В ₃. В результате преобразований получим матрицу

.

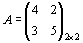a = max (2, 3) = 3, b = min (4, 5) = 4, a ¹ b, .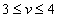

Сведение матричной игры к задаче линейного программирования

Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным методом и, наоборот, каждая задача линейного программирования может быть представлена как конечная игра двух лиц с нулевой суммой.

Рассмотрим игру двух лиц с нулевой суммой, заданную платежной матрицей

.

Если платежная матрица не имеет седловой точки, т.е. a <b и 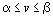, то решение игры представлено в смешанных стратегиях (x ₁, x ₂,..., x_m) и 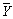(y ₁, y ₂,..., y_n).

Применение первым игроком оптимальной стратегии _опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры.

, .

Рассмотрим задачу отыскания оптимальной стратегии игрока А, для которой имеют место ограничения

Величина v неизвестна, однако можно считать, что цена игры v > 0. Последнее условие выполняется всегда, если все элементы платежной матрицы неотрицательны, а этого можно достигнуть, прибавив ко всем элементам матрицы некоторое положительное число. Преобразуем систему ограничений, разделив все члены неравенств на v.

(1)

где

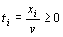, . (2)

По условию x ₁ + x ₂ + … + x _m = 1. Разделим обе части этого равенства на v.

.

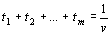Оптимальная стратегия (x ₁, x ₂,..., x_m) игрока А должна максимизировать величину v, следовательно, функция

(3)

должна принимать минимальное значение.

Таким образом, получена задача линейного программирования: найти минимум целевой функции (3) при ограничениях (1), причем на переменные наложено условие неотрицательности (2). Решая ее, находим значения , и величину1/ v, затем отыскиваются значения x _i = vt _i.

Аналогично для второго игрока оптимальная стратегия _опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры.

, .

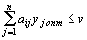Рассмотрим задачу отыскания оптимальной стратегии игрока B, для которой имеют место ограничения

Преобразуем систему ограничений, разделив все члены неравенств на v.

(4)

где

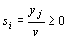, . (5)

По условию y ₁ + y ₂ + … + y _n = 1. Разделим обе части этого равенства на v.

.

Оптимальная стратегия (y ₁, y ₂,..., y_n) игрока В должна минимизировать величину v, следовательно, функция

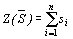(6)

должна принимать максимальное значение.

Получена задача линейного программирования: найти максимум целевой функции (6) при ограничениях (4), причем на переменные наложено условие неотрицательности (5).

Таким образом, для нахождения решения игры имеем симметричную пару двойственных задач линейного программирования. Можно найти решение одной из них, а решение второй находится с использованием теории двойственности.

Пример. Найти решение игры, заданной матрицей

.

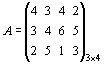a = max (2, 3, 1) = 3, b = min (4, 5, 6, 5) = 4, a ¹ b, .

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.

Для определения оптимальной стратегии игрока А имеем следующую задачу линейного программирования:

,

, .

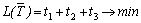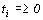Для нахождения оптимальной стратегии игрока В имеем следующую задачу линейного программирования:

,

, .

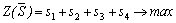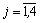Оптимальные решения пары двойственных задач имеют вид

, , .

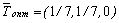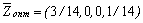Учитывая соотношения между x _i и t _i, y _j и s_j, а также равенство

,

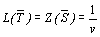можно найти оптимальные стратегии игроков и цену игры:

(1/2, 1/2, 0), 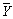(3/4, 0, 0, 1/4), v =7/2.

Игры с природой

В рассмотренных выше матричных играх предполагалось, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т. д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с природой. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно.

Условия игры задаются матрицей

.

Пусть игрок Аимеет стратегии А ₁, А ₂, …, А_m, а природа – состояния В ₁, В ₂, …, В_n. Наиболее простой является ситуация, когда известна вероятность p_j каждого состояния природы В_j. При этом, если учтены все возможные состояния, p ₁ + p ₂ + … + p_j + … + p_n = 1.

Если игрок Авыбирает чистую стратегию А_i, то математическое ожидание выигрыша составит p ₁ a_{i 1} + p ₂ a_{i 2} + … + p_n a_in. Наиболее выгодной будет та стратегия, при которой достигается

(p ₁ a_{i 1} + p ₂ a_{i 2} + … + p_n a_in).

Если информация о состояниях с природой мала, то можно применить принцип недостаточного основания Лапласа, согласно которому можно считать, что все состояния природы равновероятностны:

,

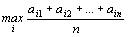т.е. стратегию, для которой среднее арифметическое элементов соответствующей строки максимальное.

Имеется ряд критериев, которые используются при выборе оптимальной стратегии. Рассмотрим некоторые из них.

1. Критерий Вальда. Рекомендуется применять максиминную стратегию. Она выбирается из условия

и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека способом.

2. Критерий максимума. Он выбирается из условия

.

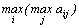Критерий является оптимистическим, считается, что природа будет наиболее благоприятна для человека.

3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

,

где a - степень оптимизма и изменяется в диапазоне [0, 1].

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При a = 1 критерий превращается в критерий Вальда, при a = 0 - в критерий максимума. На a оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем больше последствия ошибочных решений, больше желания застраховаться, тем a ближе к единице.

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

.

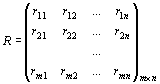Элементы матрицы рисков находятся по формуле

,

где - максимальный элемент в столбце исходной матрицы.

Оптимальная стратегия определяется выражением

.

При принятии решений в условиях неопределенности следует оценивать различные варианты с точки зрения нескольких критериев. Если рекомендации совпадают, можно с большей уверенностью выбрать наилучшее решение; если рекомендации противоречат друг другу, окончательное решение надо принимать с учетом его сильных и слабых сторон.

Пример. Возможно строительство четырех типов электростанций: А ₁ (тепловых), А ₂ (приплотинных), А ₃ (бесшлюзовых), А ₄ (шлюзовых). Состояния природы обозначим через Р ₁, Р ₂, Р ₃, Р ₄. Экономическая эффективность строительства отдельных типов электростанций изменяется в зависимости от состояния природы и задана матрицей

.

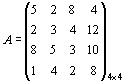1) Согласно критерию Вальда

,

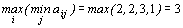следует строить бесшлюзовую электростанцию.

2) Воспользуемся критерием Сэвиджа. Построим матрицу рисков:

.

Согласно критерию Сэвиджа определяем

.

В соответствии с этим критерием также предлагается строить бесшлюзовую электростанцию.

3) Воспользуемся критерием Гурвица. Положим a=1/2.

,

т.е. следует принять решение о строительстве приплотинной электростанции.

4) Если принять известным распределение вероятностей для различных состояний природы, например считать эти состояния равновероятностными (р ₁= р ₂= р ₃= р ₄=1/4), то для принятия решения следует найти математические ожидания выигрыша:

,

,

,

.

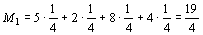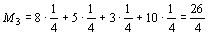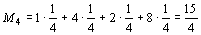Так как максимальное значение имеет М ₃, то следует строить бесшлюзовую электростанцию.

Дата добавления: 2014-12-27