Модель управления запасами, учитывающая скидки

Уравнение общих затрат для ситуации, когда учитываются затраты на покупку товара, имеет вид

[руб./ед.t],

где с – цена товара [руб./ед.тов.]; 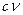– затраты на покупку товара в единицу времени [руб./ед.t]. Если цена закупки складируемого товара постоянна и не зависит от Q, то ее включение в уравнение общих затрат приводит к перемещению графика этого уравнения параллельно оси Q и не изменяет его формы. Т.е. в случае постоянной цены товара ее учет не меняет оптимального решения .

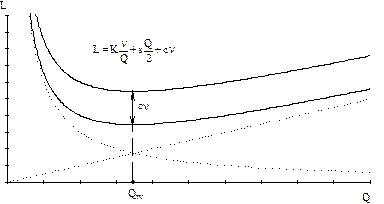
График затрат на УЗ с учетом затрат на покупку

Если на заказы большого объема предоставляются скидки, то заказы на более крупные партии повлекут за собой увеличение затрат на хранение, но это увеличение может быть компенсировано снижением закупочной цены. Таким образом, оптимальный размер заказа может изменяться по сравнению с ситуацией отсутствия скидок. Поэтому затраты на приобретение товара необходимо учитывать в модели покупок со скидками.

Новые входные параметры модели, учитывающей скидки

1) 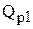, 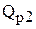– точки разрыва цен, т.е. размеры покупок, при которых начинают действовать соответственно первая и вторая скидки, [ед.тов.];

2) с, , 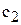– соответственно исходная цена, цена с первой скидкой, цена со второй скидкой, [руб./ед.тов.].

Чтобы определить оптимальный размер заказа , необходимо проанализировать, в какую из трех областей попадает точка разрыва цены 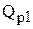. Правило выбора для случая с одной скидкой имеет вид:

Правильность решения задач с УЗ со скидками в большой степени определяется качественно построенным графиком общих затрат с указанием на графике всех параметров, используемых при решении. Поэтому в первую очередь необходимо анализировать ситуацию графически и только после этого проводить численные вычисления. Например, если внимательно проанализировать ситуации, то можно принимать решение без непосредственного использования правила. Зрительно легко определить более "выгодный" объем заказа, найдя точку, координата которой по оси L лежит ниже других вариантов заказов.

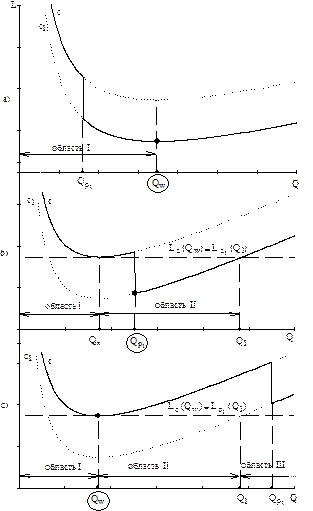
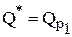График затрат с учетом скидок: a) ; b) ; с)

При решении задач с двумя скидками сначала находится оптимальный объем заказа с учетом первой скидки, а затем рассматривается вторая скидка, т.е. обе подзадачи решаются по тому же правилу.

Пример. Пусть затраты на заказ равны 10 руб., затраты на хранение продукции 1 руб. в сутки, интенсивность потребления товара 5 шт. в день, цена товара – 2 руб. за штуку, а при объеме закупки 15 шт. и более – 1 руб. Определите оптимальный размер заказа, цену покупки и затраты на УЗ.

Решение. Начинаем решение с приблизительного построения пунктирными линиями графиков двух функций общих затрат, соответствующих двум ценам, которые указываем над соответствующими линиями затрат: руб./шт. и руб./шт.

Поскольку объем заказа, задаваемый формулой Уилсона, легко определяется зрительно как точка минимума обеих функций, то без предварительных вычислений графически находим объем Уилсона и отмечаем его на графике.

Только после этого, используя параметры 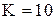руб., шт. в день, руб. за 1 шт. в сутки, вычисляем значение и подписываем его на графике под обозначением . [шт.].

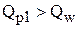Очевидно, что в область I шт. не попадает, т.к. . Таким образом, может попасть в области II или III. Границей между этими областями служит размер заказа 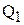, уравнивающий общие затраты при цене со скидкой 1 руб./шт. и затраты при заказе по исходной цене 2 руб./шт. Сначала строим 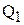графически.

Только после этого найдем 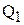численно. Используя рис., запишем выражение, показывающее равенство затрат, 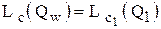, с численными значениями параметров: .

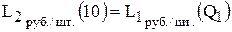Для раскрытия левой и правой частей получаем

[руб./сут.],

,

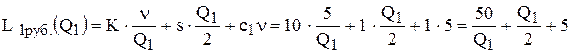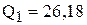, , шт. или шт.

Всегда выбираем больший из корней 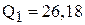, т.к. меньший по значению корень не дает нам информации о границе областей II и III, и отмечаем численное значение 26,18 на графике.

Таким образом, точка разрыва цен попадает в область II, т.к.

().

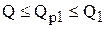Отметим эту точку на графике в любом месте области II.

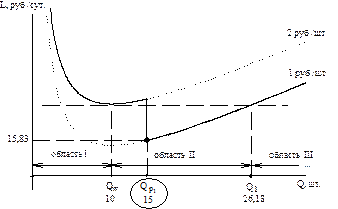
После этого сплошной линией обведем те участки обеих функций затрат, которые соответствуют действующим ценам, т.е. до объема обведем верхнюю линию затрат, а после – нижнюю.

Согласно правилу и графику оптимальным является объем заказа 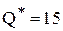шт. по цене 1 руб./шт. Таким образом, в данной ситуации скидкой пользоваться выгодно. Общие затраты при этом составляют 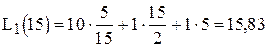[руб./сут.]. Если бы заказывали по 10 шт. товара, то общие затраты составили бы 20 рублей, т.е. при заказе в 15 шт. экономия средств составляет 4,17 рублей в сутки.

Пример. Пусть поставщик супа в пакетах предоставляет следующие скидки

Размер заказа	Цена, руб./шт.
1–199
200–499	1,96 (2% скидки)
500 и более	1,92 (4% скидки)

Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на УЗ?

Решение. Строим пунктирными линиями графики трех функций затрат и обозначаем на них соответствующие цены , и 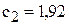. Строим на графике точку, соответствующую .

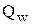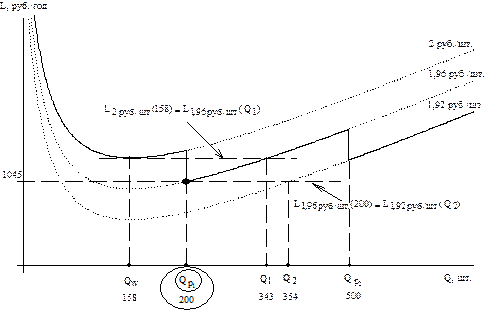
1. Вычисляем значение 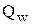=158, отмечаем это значение на графике.

2. Поскольку 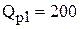не попадает в область I, то необходимо найти границу областей II и III. Для этого строим на графике уровень затрат, соответствующий заказу 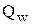и цене с=2 руб. до пересечения со второй линией затрат, и графически находим и строим .

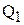4. Находим 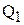численно, используя выражение

или ; 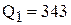[шт.].

5. Используя правило и график, находим более дешевый объем заказа (с учетом только первой скидки) 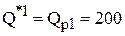[шт.].

6. Чтобы рассмотреть вторую скидку, построим на графике уровень затрат, соответствующий заказу, оптимальному при действии только первой скидки, т.е. 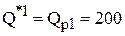и цене руб./шт. При пересечении этого уровня и третьей линии общих затрат графически определяем .

7. Находим численно =354, исходя из выражения

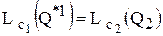или .

8. Используя правило и график затрат, находим наиболее дешевый объем заказа с учетом первой и второй скидок 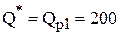шт.

9. Таким образом, пользоваться второй скидкой владельцу магазина невыгодно. Оптимальный для него вариант – заказывать 200 пакетов по цене 1,96 руб./шт. обойдется в 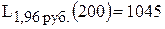[руб./год].

Дата добавления: 2014-12-27