Получение математических моделей методами теории корреляции

Содержание и порядок выполнения работы

1 Строят матрицу полного факторного эксперимента (ПФЭ) в соответствии с общими правилами построения матриц.

2 Для удобства расчётов строят таблицу 2.11.

Таблица 2.11 – Исходные данные и результаты расчёта математической модели

Точка плана V	Текущие значения параметра оптимизации	Среднее значение уV	Дисперсия опыта	Значения по модели	Дисперсия адекват-ности ()^2
у1	у2	у3
…

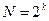
3 Уравнение регрессии записывают в виде

, (2.37)

где 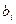– коэффициент регрессии;

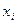– независимые переменные.

Коэффициенты регрессии рассчитывают по формуле

, (2.38)

где 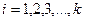– номер фактора;

– среднее значение параметра оптимизации, полученное по результатам эксперимента;

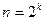– минимальное количество опытов.

4 Определяют дисперсию, которая характеризует ошибку опыта

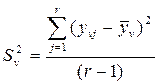, (2.39)

где – текущее значение параметра оптимизации (у₁, у₂, у₃);

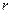– число повторных опытов в каждой строчке матрицы ПФЭ.

Значения записывают в таблицу 2.11.

5 Определяют дисперсию параметра оптимизации, которая является средним арифметическим из дисперсии 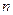различных вариантов исследований

. (2.40)

6 Выполняют проверку однородности дисперсий по критерию 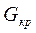Кохрена. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий

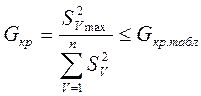, (2.41)

где – табличные значения критерия Кохрена, которые приведены в таблице А1 (Приложение А).

В соответствии с таблицей для числа степеней свободы числителя и знаменателя 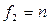определяют . Дисперсии считают однородными, если экспериментальные значения критерия Кохрена не превышают табличных .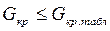

7 Рассчитывают дисперсию коэффициента регрессии

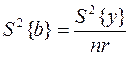. (2.42)

8 Проверяют значимость коэффициентов регрессии по критерию Стьюдента

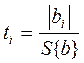. (2.43)

Расчётные значения сравнивают с табличными 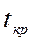, которые выбирают при заданном уровне значимости и числе степеней свободы (таблица А2 (Приложение А)). Если 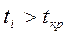, то коэффициент считают значимым, в противном случае – не значимыми.

9 Рассчитывают значения . Для этого используют значимые коэффициенты уравнения регрессии т соответствующие номеру опыта строки матрицы ПФЭ. Значения записывают в таблицу 2.11.

10 Рассчитывают дисперсию адекватности

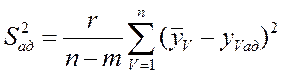, (2.44)

где m –число значимых коэффициентов уравнения регрессии.

11 Проверяют адекватность полученной математической модели по критерию Фишера

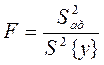. (2.45)

Если расчётные значения , то считают, что полученная математическая модель адекватна, значения выбирают при уровне значимости 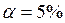, числе степеней свободы числителя и числе степеней свободы знаменателя 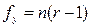(таблица А3) (Приложение А).

Если отношение меньше единицы, то условие 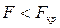выполняется для любого числа степеней свободы.

2.4.2 Содержание отчёта

1 Название и цель работы.

2 Исходные данные для получения математической модели.

3 Матрица планирования эксперимента.

4 Результаты расчёта коэффициентов регрессии .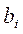

5 Результаты расчёта дисперсии опыта, дисперсии адекватности и дисперсии коэффициента регрессии с проверкой по критерию Кохрена, (таблица 2.11).

6 Проверка значимости коэффициентов регрессии по критерию Стьюдента.

7 Результаты расчёта дисперсии адекватности 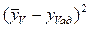(таблица 2.11).

8 Проверка адекватности математической модели по критерию Фишера.

9 Выводы.

2.4.3 Контрольные вопросы

1 Что называют параметром оптимизации при полном факторном эксперименте (ПФЭ)?

2 Что называют факторами при ПФЭ? Как выбирают интервалы измерения факторов?

3 Что называют полным факторным экспериментом?

4 Как определяют минимальное количество опытов при ПФЭ?

5 Назовите основные принципы построения матриц ПФЭ.

6 Какие свойства имеет матрица ПФЭ?

7 Как рассчитывают коэффициенты регрессии?

8 Как определяют дисперсию, характеризующую ошибку опыта?

9 Как проверяют однородность дисперсии?

10 Как проверяют значимость коэффициентов регрессии?

11 Как проверяют адекватность модели?

Дата добавления: 2014-12-27