Формула Байеса

Пусть произведен эксперимент, в результате которого событие А наступило. Вероятность события А можно вычислить по формуле (4.13). Эта дополнительная информация позволяет произвести переоценку вероятностей гипотез H_i, вычислив Р(H_i /А). По теореме умножения вероятностей:

Р(А Hi) = Р(А) × Р(Hi/А) = Р(Hi) × Р(А/Hi).

(4.14)

Откуда:

,

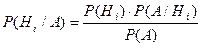или, вычислив Р(А) по формуле полной вероятности (4.13), получим:

.

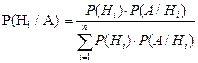(4.15)

Формулу (4.15) называют формулой Байеса. Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в результате которого появилось событие А.

Пример 16.

Условие из примера 15. Событие А уже произошло. Вызванный наугад студент оказался отличником. Найти вероятность того, вызванный наугад студент оказался отличником из первой группы Р(H₁/А).

Решение.

Вероятность Р(А/H₁) события «вызван студент-отличник при условии, что он является отличником из первой группы». Аналогично вероятность Р(А / H₂) из второй группы. По формуле Байеса (4.15) получаем:

4.7. Вопросы для самоконтроля по теме «Основы теории вероятностей»

1. Определите правильный ответ:

В урне 200 билетов. Из них 10 выигрышных. Вероятность того, что первый вынутый билет окажется выигрышным, равна:

a) 0,02; b) 0,05; c) 0,2; d) 0,01.

2. Определите правильный ответ:

Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав три выстрела, он хотя бы раз попадёт в цель?

a) 0,999; b) 0,992; c) 0,92; d) 0,8.

3. Определите правильный ответ:

Станок-автомат производит изделия трех сортов. Первого сорта – 80%, второго – 15%. Чему равна вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта?

a) 0,2; b) 0,95; c) 0,8; d) 0,15.

4. Определите правильный ответ:

Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав три выстрела, он ни разу не попадёт?

a) 0,08; b) 0,4; c) 0,6; d) 0,008.

5. Определите правильный ответ:

В книжной лотерее разыгрывается 5 книг. Всего в урне имеется 30 билетов. Первый подошедший к урне вынимает билет. Определить вероятность того, что билет окажется выигрышным.

a) 5/30; b) 1/30; c) 0,2; d) 0,1.

6. Определите правильный ответ:

При наборе телефонного номера абонент забыл последнюю цифру и набрал ее наудачу, помня только, что эта цифра нечётная. Найти вероятность того, что номер набран правильно.

a) 1/9; b) 1/7; c) 1/5; d) 1/3.

7.Определите правильный ответ:

Для посева берут семена из двух пакетов. Вероятность прорастания семян в первом пакете равна 0,4, а во втором 0,5. Взяли по одному семени из каждого пакета, тогда вероятность того, что оба они прорастут, равна:

a) 0,9; b) 0,45; c) 0,3; d) 0,2.

8. Определите правильный ответ:

Вероятность того, что в этом году будет хороший урожай апельсинов, равна 0,9, а лимонов – 0,7. Тогда вероятность того, что уродятся и апельсины и лимоны, равна:

a) 0,8; b) 0,3; c) 0,63; d) 0,5.

9. Определите правильный ответ:

Вероятность вытащить бракованную деталь из первого ящика равна 0,2, а из второго – 0,3. Из каждого ящика взяли по одной детали. Тогда вероятность того, что обе они бракованные, равна:

a) 0,06; b) 0,5; c) 0,25; d) 0,1.

10. Определите правильный ответ:

Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0,8, у другого – 0,9. Найти вероятность того, что цель не будет поражена ни одной пулей.

a) 0,2; b) 0,02; c) 0,3; d) 0,15.

Глава 5. Случайные величины

Дата добавления: 2014-12-27