
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические операции. Истинностные значения новых высказываний определяются при этом только истинностными значениями входящих в них высказываний
|
|
|
|
Истинностные значения новых высказываний определяются при этом только истинностными значениями входящих в них высказываний. Построение из данных высказываний (или из данного высказывания) нового высказывания называется логической операцией. Знаки логических операций называются логическими связками. Логические связки могут быть: одноместными (унарными), двухместными (бинарные), трехместными (тернарными) и т.д.
Пример 10.
- Из высказываний «х > 2», «х < 3» при помощи связки «и» можно получить высказывание «x > 2 и х < 3»;
- из высказываний «у > 10», «х < 3» при помощи связки «или» можно получить высказывание «у > 10 или х < 3»;
- из высказываний «х > 2», «у < 3» при помощи связки «если..., то...» можно получить высказывание «если x > 2, то у < 3».
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности. В таблице 1 представлена таблица истинности для операции «отрицание» («инверсия»).
Таблица истинности для операции «отрицания»
Таблица 1
| А | не А |
В таблице 2 приведены основные бинарные логические операции и связки.
Основные бинарные логические операции и связки
Таблица 2
| Обозначение логической операции | Другие обозначения логической операции | Название логической операции и связки | Примечание (читается) |
| А1 Ù А2 | А1 & А2 А1 × А2 А1А2 | конъюнкция, логическое умножение, логическое «и» | А1 и А2 |
| А1 Ú А2 | А1 + А2 | дизъюнкция, логическое сложение, логическое «или» | А1 или А2 |
| А1 ® А2 | А1 Ê А2 А1 Þ А2 | импликация, логическое следование | если А1, то А2; А1 имплицирует А2; А1 влечет А2 |
| А1 Å А2 | А1 + А2 А1 Ú А2 А1 D А2 | сумма по модулю 2, разделительная дизъюнкция, разделительное «или» | А1 плюс А2; либо А1, либо А2 |
| А1 ~ А2 | А1 º А2 А1 «А2 А1 Û А2 | эквиваленция, эквивалентность, равнозначность, тождественность | А1 тогда и только тогда, когда А2; А1 эквивалентно А2 |
| А1 ½ А2 | штрих Шеффера, антиконъюнкция | неверно, что А1 и А2; А1 штрих Шеффера А2 | |
| А1 ¯ А2 | А1 °А2
А1 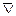 А2 А2
| стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера | ни А1, ни А2; А1 стрелка Пирса А2 |
Примечание: А1 и А2 являются высказываниями.
Связки и частица «не» рассматриваются в алгебре логики как операции над величинами, принимающими значения 0 (ложь/false) и 1 (истина/true), и результатом применения этих операций также являются числа 0 или 1. В таблице 3 представлены все наборы значений переменных А1 и А2 и значения функций на этих наборах.
Таблица истинности для основных бинарных логических операций
Таблица 3
| А1 | А2 | Ù | Ú | ® | Å | ~ | ½ | ¯ |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 452; Нарушение авторских прав?; Мы поможем в написании вашей работы!