
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебраическая проблема собственных значений
|
|
|
|
Обращение матриц
Отыскание матрицы, обратной заданной матрице A, основывается на тождестве
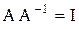 , (5.51)
, (5.51)
где  - единичная матрица. Это матричное равенство можно рассматривать как n СЛАУ относительно n неизвестных векторов, являющихся столбцами матрицы
- единичная матрица. Это матричное равенство можно рассматривать как n СЛАУ относительно n неизвестных векторов, являющихся столбцами матрицы  . Таким образом, задача обращения матрицы эквивалентна задаче решения n СЛАУ с одной и той же матрицей, но с разными правыми частями.
. Таким образом, задача обращения матрицы эквивалентна задаче решения n СЛАУ с одной и той же матрицей, но с разными правыми частями.
6.1. Постановка задачи
Рассматривается матричное (векторное) уравнение
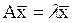 ,(6.1)
,(6.1)
для которого ищется решение - ненулевой вектор 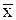 и значение параметра
и значение параметра 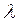 ,.при котором это решение существует. Такое значение
,.при котором это решение существует. Такое значение 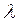 называется собственным значением матрицы
называется собственным значением матрицы 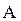 , а вектор
, а вектор 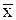 - ее собственным вектором.
- ее собственным вектором.
После записи уравнения (1) в виде
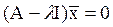 , (6.2)
, (6.2)
где матрица  называется характеристической матрицей, легко видеть, что ненулевое решение существует, если
называется характеристической матрицей, легко видеть, что ненулевое решение существует, если
 (6.3)
(6.3)
Уравнение (3) относительно искомого параметра 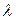 называется характеристическим уравнением и после раскрытия определителя приобретает вид алгебраического уравнения n-й степени, которое:
называется характеристическим уравнением и после раскрытия определителя приобретает вид алгебраического уравнения n-й степени, которое:
 , (6.4)
, (6.4)
которое имеет n корней, собственных значений,  . Многочлен
. Многочлен 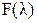 называется характеристическим многочленом. Подставив каждое из собственных значений в матричное уравнение (2) и решив его, можно найти собственные вектора
называется характеристическим многочленом. Подставив каждое из собственных значений в матричное уравнение (2) и решив его, можно найти собственные вектора  ,.
,.
Если ищутся все n собственных значений и векторов, то говорят о полной проблеме собственных значений, если же интересуются только некоторыми собственными значениями, то это - частичная проблема собственных значений.
Все методы решения проблемы собственных значений можно разделить на две группы:
1) методы, непосредственно решающие нелинейное уравнение (3) или (4);
2) методы, преобразующие задачу определения собственных значений матрицы 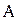 в задачу определения собственных значений матрицы специального вида, например, треугольной или диагональной.
в задачу определения собственных значений матрицы специального вида, например, треугольной или диагональной.
|
|
|
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 795; Нарушение авторских прав?; Мы поможем в написании вашей работы!