Простые ссудные проценты

Как правило, простые проценты применяют в краткосрочных финансовых операциях, либо когда после каждого интервала начисления процентные деньги выплачиваются кредитору.

Величина процентов зависит от трех параметров: первоначальной суммы, процентной ставки и периода начислений:

I = P i n, (1)

где I – процентные деньги (проценты);

i – процентная ставка. В расчетах фиксируется в виде десятичной или натуральной дроби;

n – период начисления;

P – первоначальная сумма.

Процентная ставка и период начисления должны быть согласованы по времени. Так, если известна годовая процентная ставка, то и период начисления должен быть выражен в виде количества лет, либо долей года (если он меньше года).

Пример 1.

На депозитный счет внесена сумма 100 тыс. руб. под 12 % годовых. Каким будет доход вкладчика через год?

Решение.

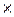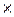Доход вкладчика или проценты по вкладу рассчитывают по формуле (1): I = P i n = 100 0,12 1=12 (тыс. руб.).

Чтобы найти наращенную сумму, надо к первоначальной сумме прибавить проценты:

S = P + I, (2)

где S – наращенная или будущая сумма.

В приведенном выше примере накопленная на счете сумма к концу года составит: S = 100 + 12 = 112 тыс. руб.

На основе формул (1) и (2) можно вывести базовую формулу простых процентов:

S = P + I = P + P i n = P (1 + i n) (3)

Вернемся к примеру и найдем наращенную сумму, используя формулу простых процентов: S = 100 (1 + 0,12 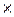1) = 112 тыс. руб.

В примере период начисления составляет ровно 1 год. Если этот параметр меньше года, то его следует представить в виде доли года.

Так, если период начисления установлен в месяцах, надо его превратить в доли года, разделив на 12 (месяцев в году). Если период установлен в днях, то чтобы превратить в доли года, надо его разделить на 360 или 365 (дней в году). В зависимости от того, какое количество дней в году принято в расчет, различают точные или обыкновенные проценты.

Если в расчетах принято, что год равен 360 дням, а месяц – 30 дням, то речь идет об обыкновенных процентах. Если год принят равным 365 дням (а високосный – 366 дням), соответственно продолжительность месяца может быть 30 и 31 день (28 или 29 дней в феврале), то рассчитанные проценты будут называться точными.

Пример 2.

Рассчитать обыкновенный и точный процент по 60-дневному займу в 300 тыс. руб., если ссудная процентная ставка равна 8 %.

Решение.

Обыкновенный процент I = P i n = 300 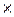0,08 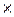= 4 тыс. руб.

Точный процент I = 300 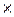0,08 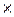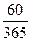= 3,95 тыс. руб.

Заметьте, что обыкновенный процент больше точного процента. Его легче рассчитать, если нет калькулятора.

Еще одна проблема возникает, когда не известен период начисления, но установлены календарные даты. Для определения периода надо рассчитать количество дней между этими датами.

Например, ссуда выдана 5 марта со сроком погашения 28 сентября. Чтобы найти период ссуды, надо вычислить интервал между 28 сентября и 5 марта. Лучше всего воспользоваться так называемым банковским календарем (прил. 1).

Находим порядковый номер каждой даты: 28 сентября – 271^ый день года, а 5 марта – 64^ый день года. Разница между этими числами и есть период начисления, выраженный в днях: 271 – 64 = 207 дней. Теперь надо период, выраженный в днях, превратить в доли года, т.е. 207: 365 = 0,567 года. Мы получим значение параметра n, которое следует подставить в соответствующую формулу.

Пример 3.

7 января на счет зачислено 4 тыс. руб., 25 февраля к этой сумме было добавлено 2 тыс. руб., а 10 июня внесено еще 2,4 тыс. руб. Какая сумма будет накоплена на счете к 30 июня, если банк применяет годовую процентную ставку 10 %?

Решение.

Для решения задачи воспользуемся временной диаграммой (рис. 2).

Согласно календарю 30 июня – 182^ой день, 7 января – 7^ой день, 25 февраля – 56^ой день и 10 июня – 162^ой день года. Следовательно, проценты будут начисляться по первому вкладу в течение 175 дней, по второму – 126 дней, по третьему – 20 дней.

07. 01. 25. 02. 10. 06. 30. 06

Рис. 2. Временная диаграмма примера 3

Воспользовавшись формулой (3), находим ответ:

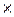
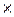
S = 4 (­1 + 0,1 ) + 2 (1 + 0,1 ) + 2,4 (1+0,1 ) =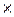

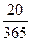= 4,19 + 2,07 + 2,41 = 8,67 тыс. руб.

Величина, показывающая во сколько раз наращенная сумма превышает первоначальную, называется коэффициентом наращения (k_н):

k_н = 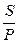= = ( 1 + in). (4)

Зная будущую сумму, можно найти ее исходное значение:

P = 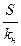= (5)

Определение первоначальной суммы относительно будущей называется дисконтированием.

Величина, показывающая во сколько раз первоначальная сумма меньше наращенной (будущей), называется коэффициентом дисконтирования (k_д):

k_д = (6)

Пример 4.

Заемщик взял ссуду в банке, применяющему ставку 12 %. Какую сумму он взял, если через полгода ему надо вернуть 100 тыс. руб.?

Решение.

Известны будущая сумма, процентная ставка и период начисления. Для нахождения первоначальной суммы надо продисконтировать 100 тыс. руб. на 0,5 года:

P = 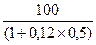= 94,34 тыс. руб.

Пользуясь базовой формулой простых процентов, можно находить любой неизвестный параметр, не только P и I, но и n, i.

i = 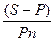(7)

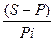n = (8)

Пример 5. Заемщик взял ссуду 150 тыс. руб. на 2 месяца. Какую процентную ставку применил банк, если сумма к погашению составила 200 тыс. руб.?

Решение.

В соответствии с формулой (7) i = 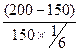= 2 или 200 %.

Иногда требуется погасить несколько обязательств единовременно одним платежом, который должен быть эквивалентен этим долговым обязательствам. Например, заемщик имеет перед одним и тем же кредитором два долга: 20 тыс. руб., которые нужно погасить через полгода, и 50 тыс. руб. – через год. У него есть средства, чтобы погасить оба обязательства сейчас. Какой платеж ему следует сделать, если кредитор применил ставку 20 % годовых?

Вспомним правило, что нельзя складывать разновременные суммы. Сначала их надо привести к одной точке во времени, т.е. одной и той же временной базе.

Построим временную диаграмму, в качестве точки локализации целесообразно принять сегодняшнюю дату, т.е. дату, когда заемщик собирается погасить долг.

Рис. 3. Временная диаграмма единовременного погашения нескольких долгов

Продисконтируем каждый долг на соответствующий период (полгода и год), а затем, когда найдем значения в точке «сейчас», т.е. в одной временной базе, можно будет сложить оба долга.

Р₁ = 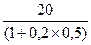= 18,18 тыс. руб.

Р₂ = = 41,67 тыс. руб.

Р = Р₁ + Р₂ = 59,85 тыс. руб.

Таким образом, сегодня заемщик должен заплатить кредитору 59,85 тыс. руб. и тем самым погасить оба долга.

Предположим, что у заемщика нет возможности погасить свои долги ни сейчас, ни через полгода. Он получил согласие кредитора рассчитаться с ним через год. Какую сумму заемщик заплатит кредитору?

В этом случае за временную базу сравнения целесообразно принять точку «1 год». Тогда обязательство в 20 тыс. руб. надо нарастить на 0,5 года, а обязательство в 50 тыс. руб. в этой точке останется неизменным.

Рис. 4. Временная диаграмма с точкой локализации 1 год

В итоге единовременный платеж будет равен:

S = 20 (1 +0,2 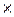0,5) + 50 = 72 тыс. руб.

В рассмотренном примере показаны три альтернативных варианта:

20 тыс. руб. сейчас и 50 тыс. руб. через год

59,85 тыс. руб. сейчас эквивалентные суммы

72 тыс. руб. через год

Следует подчеркнуть, что временная база – это произвольно выбранная точка во времени, к которой должны быть приведены все обязательства и платежи. Только в этом случае будет обеспечено требование эквивалентности.

Таким образом, есть только два направления движения денег – назад и вперед (это видно на диаграмме). Движение вперед означает наращение денежной суммы, назад – ее дисконтирование.

Пример 6.

У вас есть три долга: 200 долл. со сроком погашения через 3 месяца, 300 долл. – через полгода и 500 дол. – через год. Вы хотите погасить три долга сегодня. Ваш кредитор не возражает. Какова сумма единовременного платежа, если годовая процентная ставка по всем обязательствам одинакова и равна 12 %?

Решение.

Нарисуем временную диаграмму, приняв за х искомый платеж.

Рис. 5. Временная диаграмма примера 6

Случай 1. Примем за дату сравнения точку 0, т.е. «сейчас». И приведем все суммы к этой точке, затем сложим их и найдем искомую величину.

Рис. 6. Временная диаграмма 1 ^го случая

Движение назад означает, что необходимо применить дисконтирование (5).

х = =

= 194,17 + 283,02 + 446,43 = 923,62 долл..

Случай 2. Пусть базой сравнения будет дата погашения первого долга – 3 месяца. Приведем все обязательства и платеж к этой точке, т.е. платеж х надо нарастить на 3 месяца, первый долг остается неизменным, второй долг надо продисконтировать на 3 месяца (срок между датой погашения и точкой локализации), третий долг надо также продисконтировать, но на 9 месяцев (12 - 3).

х (1+0,12 ;

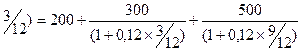1,03 х = 200 + 291,26 + 458,72;

х = 922,31 долл.

х дол. 200 дол. 300 дол. 500 дол.

6 мес.

3 мес.

		12 мес.

3 мес.

3 мес.

9 мес.

Рис. 7. Временная диаграмма 2 ^го случая

Случай 3. Пусть базой сравнения будет дата погашения второго долга – 6 месяцев.

x дол. 200 дол. 300 дол. 500 дол.

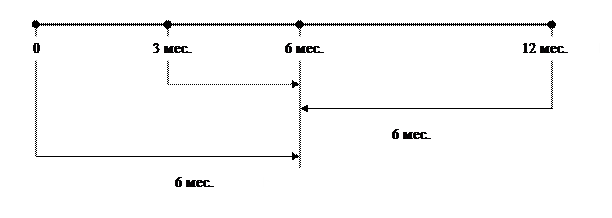
Рис. 8. Временная диаграмма 3 ^го случая

х (1+0,12 ;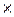

1,06 х = 206 + 300 + 471,7;

х = 922,36 долл.

Случай 4. Примем за базу сравнения дату погашения третьего долга – 12 месяцев.

х (1 + 0,12 1) = 200 (1+0,12 ;

1,12 х = 218 + 318 + 500;

х = 925 долл.

x дол. 200 дол. 300 дол. 500 дол.

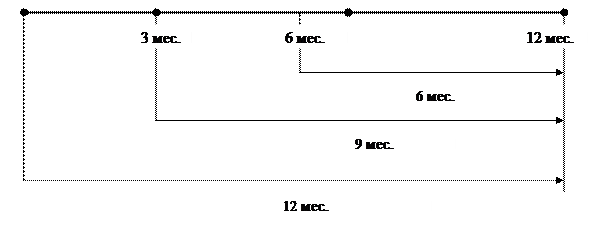
Рис. 9. Временная диаграмма 4 ^го случая

Во всех четырех случаях мы нашли величину единовременного платежа, который заемщик должен выплатить сейчас, чтобы погасить три долга сразу.

Как можно заметить, результаты расчетов хоть незначительно, но различаются. На это повлияла база сравнения. Чтобы избежать конфликтных ситуаций, временная база должна оговариваться заранее.

Задания для самоподготовки

Контрольные вопросы

1. Что является предметом изучения финансовой математики?

2. Чем различаются способы начисления процентов?

3. Что такое проценты?

4. Что представляет собой процентная ставка?

5. Что такое период начисления?

6. Что представляет собой временная диаграмма?

7. Почему нельзя складывать разновременные суммы?

8. Чем различаются простые и сложные проценты?

9. Что такое временная база сравнения?

10. От чего зависит величина процентов?

11. Как рассчитать наращенную сумму?

12. В чем различие между обыкновенными и точными процентами?

13. Что представляет собой коэффициент наращения?

14. Что такое дисконтирование?

15. Какая имеется связь между коэффициентами наращения и дисконтирования?

Дата добавления: 2014-12-27