
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Базис подпространства Крылова. Ортогонализация Арнольди
|
|
|
|
Для построения базиса в пространстве Крылова Km (n 1, A) можно применить следующий подход. Сначала находят векторы w 1= n 1, w 2= Aw 1, w 3= A 2 w 1= Aw 2,…, w m = A m –1 w 1= Aw m –1. По определению (2.21),
| Km (n1, A)=span{w1, w2,…,w m }. |
Далее переходят от { w 1, w 2,…, w m } к { n 1, n 2,…, n m }, применив процедуру ортогонализации
n k +1=w k –1– 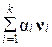 , ,
| (2.26) |
и затем пронормировав полученные векторы. Предполагая, что предыдущие k векторов уже построены, т.е.
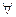 i, j (1£ i, j £ k): (n i,n j)= i, j (1£ i, j £ k): (n i,n j)= 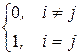 . .
| (2.27) |
Тогда (2.26) можно записать
n k +1=An k – 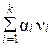 . .
|
Для выполнения условия ортогональности n k +1 ко всем предыдущим векторам, умножают это равенство скалярно на n j (j £ k) и приравнивая результат к нулю
(An k, n j)– 
| (2.28) |
С учетом (2.27) отсюда легко получить выражение для коэффициентов a j
| a j =(An k, n j). |
Описанный метод может быть оформлен в виде следующей процедуры, называемой ортогонализацией Арнольди.
Алгоритм ортогонализации Арнольди
| Входные данные: n1, такой что ||n1||2=1; A; m |
| Выполнять для j =1,…, m |
| w=An j |
| Выполнять для i =1,…, j |
| hij =(w, n i) |
| w=w– hij n i |
| увеличить i |
| hj +1, j =||w||2 |
| Если hj +1, j =0, то КОНЕЦ. Базис построен. |
| n j +1=w/ hj +1, j |
| увеличить j |
Для коэффициентов ортогонализации здесь введена двойная индексация, с учетом которой внутренний цикл алгоритма алгебраически записывается как
h j +1, j n j +1=An j –  . .
| (2.29) |
Коэффициенты ортогонализации hi , j можно объединить в виде матрицы H, дополнив в ней недостающие позиции нулями. При этом, как видно из алгоритма, для заданной размерности пространства m генерируется m +1 векторов. Последний вектор n m +1 (возможно, нулевой) в матричном представлении означает расширение базиса V одним дополнительным столбцом, т.е.
| V m =[n1|n2|…|n m ]; V m +1=[n1|n2|…|n m |n m +1]. |
Соответствующий вектору n m +1 коэффициент hm +1, m означает расширение матрицы H одной дополнительной строкой (возможно, нулевой).
|
|
|
Пусть 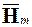 – это матрица (m +1)´ m матрица коэффициентов hm +1, m, а матрица H m – та же самая матрица без последней строки, имеющая размерность m ´ m. Тогда непосредственно из описания алгоритма Арнольди и (2.29) следует, что матрица H m является матрицей в верхней форме Хессенберга, (матрица называется верхней хессенберговой или верхней почти треугольной, если ее ненулевые элементы расположены только в ее верхнем треугольнике, на диагонали и на поддиагонали) и для нее справедливы соотношения
– это матрица (m +1)´ m матрица коэффициентов hm +1, m, а матрица H m – та же самая матрица без последней строки, имеющая размерность m ´ m. Тогда непосредственно из описания алгоритма Арнольди и (2.29) следует, что матрица H m является матрицей в верхней форме Хессенберга, (матрица называется верхней хессенберговой или верхней почти треугольной, если ее ненулевые элементы расположены только в ее верхнем треугольнике, на диагонали и на поддиагонали) и для нее справедливы соотношения
AV m =V m +1  =V m H m +w m e mT; =V m H m +w m e mT;
| (2.30) |
| V mT AV m =H m. | (2.31) |
Кроме того, вследствие ортонормальности базиса { n j } имеет место равенство
| V T n k =e k. | (2.32) |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2303; Нарушение авторских прав?; Мы поможем в написании вашей работы!