
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моменти розподілу. Визначення їх за даними досліду
|
|
|
|
Числові характеристики випадкової величини.
6.1.Основні характеристики розташування і варіації випадкової величини.
1.Математичне сподівання випадкової величини (середнє значення).
Нехай Х - дискретна випадкова величина,що приймає значення  , з ймовірностями
, з ймовірностями  -. Їх мат. сподіванням М(Х) називають величину,що дорівнює сумі добутків її можливих значень на ймовірності, з якими ці значення з’являються:
-. Їх мат. сподіванням М(Х) називають величину,що дорівнює сумі добутків її можливих значень на ймовірності, з якими ці значення з’являються:

Приклад.
На складі є 100 заготовок вагою 1кг, 20 - вагою 2кг. 5 - вагою 3кг. Визначити середню вагу заготовки. Середня вага і є мат.сподіванням (середнє значення) випадкової величини – ваги заготівки.
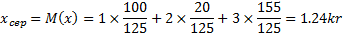
Якщо Х- неперервна випадкова величина із щільністю розподілу f(х),її математичне сподівання
визначається

Властивості математичного сподівання.
а)мат.сподівання сталої величини Х дорівнює цій величині:
M(C)=C; C=const;
б)Мат.сподівання добутку незалежних випадкових величин дорівнює добутку їх мат. сподівань:
M(X,Y,Z) = M(X) M (Y) M(Z);
Звідси виходить що сталий множник можна виносити за знак математичного сподівання:
М(СХ)=М(С)м(Х)=СМ(Х);
в) мат.сподівання алгебраїчної суми випадкових величин дорівнює сумі мат.сподівань цих величин:
M(X+Y+Z) =M(X)+M(Y)+ M(Z).
Розглянемо дві випадкові величини X і Y,що мають наступні ряди розподілу:

| -2 | -1 | |||

| 0.05 | 0.2 | 0.5 | 0.2 | 0.05 |
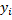
| -20 | -10 | |||

| 0.05 | 0.2 | 0.5 | 0.2 | 0.05 |
Неважко переконатися,що М(Х)=О і М(Y)=О.
Незважаючи на те, що мат. сподівання однакові, але відхилення значень тієї й іншої величини його середнього істотно відрізняються. Відхиленням називають різницю між значенням випадкової величини і її мат. сподіванням:

У теорії ймовірностей розкид значень випадкової величини, тобто сукупність варіантів ознаки, характеризують дисперсією.
|
|
|
2. Дисперсією (розсіюванням) називають мат. сподіванням квадрата відхилень випадкової величини від її мат.сподівання

Формула для обчислення дисперсії:
а) для дискретної В В (випадкової величини)

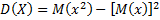
б) для неперервної В В з щільністю розподілу f(х)
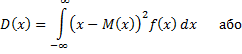
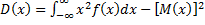 .
.
Для останнього прикладу дисперсії величин X тa Y відповідно дорівнюють D(X)=2; D (Y)=200.
Так як при зведенні до квадрату змінюється розмірність випадкової величини, для характеристики розкладу використовують величину,що дорівнює
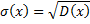
І називається середнім квадратним відхиленням або стандартом.
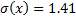
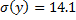 .
.
6.2.Момент розподілу.
Розглянемо дискретну випадкову величину Х, задана розподілом
| Х | ||||
| Р | 0.16 | 0.2 | 0.19 | 0.01 |
М(Х) = 1  0.16 + 2
0.16 + 2  0.2 + 5
0.2 + 5  0.19 + 100
0.19 + 100  0.01 = 2.95
0.01 = 2.95
Складемо тепер ряд із квадратів знань величини Х і знайдемо М( )
)

| ||||
| Р | 0.16 | 0.2 | 0.19 | 0.01 |

 істотно більше М (х) з наявності серед значень
істотно більше М (х) з наявності серед значень  одного, значно більшого ніж інші, хоча і має дуже малу ймовірність появи.
одного, значно більшого ніж інші, хоча і має дуже малу ймовірність появи.
Для урахування впливу таких знань в теорії ймовірності уведено моменти розподілу початкові і центральні,які узагальнюють поняття числових характеристик випадкової величини.
Початковим моментом k-го порядку називають мат. сподівання величини  ,тобто
,тобто

Для конкретної величини:

Для неперервної:
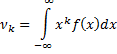
Зокрема початковий момент 1-го порядку це мат.сподівання:

Початковий момент 2-го порядку - це мат. сподівання квадрата випадкової величини:
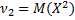 .
.
Центральним моментом k-го порядку називають математичне сподівання величини: 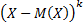
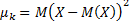
Центральний момент 1-го порядку:
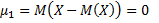
Центральний момент 2-го порядку являє собою дисперсію:
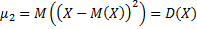
Дисперсія може бути виражена через початкові моменти:
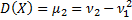
Також можна виражати і далі:
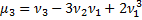

Моменти вищих порядків використовуються для опису закону розподілу.З ним зв’язані:
|
|
|
1)асиметрія
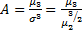 ,
,
Що характеризує несиметричність кривої щільності розподілу випадкової величини щодо її мат. сподівання:
f(x)
A=0
A<0-лівостороння асиметрія A>0-правостороння асиметрія
0 x
2)ексцес

що характеризує гостро- або плосковершиність функції розподілу:
f(x)
E>0
E=0
E<0
x
6.3.Визначення числових характеристик кількісної ознаки за дослідними даними.
Параметри статистичного розподілу
(Елементи математичної статистики).
Усі моменти розподілу випадкової величини мають свої статистичні аналоги. Це моменти статистичного розподілу і визначаються за дослідними даними.
Якщо дані згруповані у варіаційний ряд, статистичні моменти визначаються за тими же формулами що і їх теоретичні аналоги для дискретної випадкової величини, але із заміною ймовірності  на відносну частоту
на відносну частоту 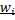 . Статистичні параметри будемо позначати *.
. Статистичні параметри будемо позначати *.
Мат. сподівання 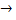 вибіркова серія:
вибіркова серія:
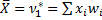 -
-
- cтатистичний момент 1-го поряку.
Дисперсія 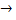 вибіркова дисперсія:
вибіркова дисперсія:
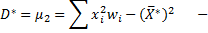
- cтатистичний центральний момент 2-го порядку.
Тут треба зробити зауваження.
1.Статистичні величини 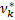 ,
, 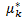 , у тому числі середня вибіркова
, у тому числі середня вибіркова  і дисперсія
і дисперсія 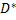 є для теоретичних величин
є для теоретичних величин 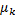 ,
, 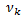 (у тому числі
(у тому числі  ,
,  ))так званими початковими точковими (точечними) оцінка, тобто оцінками, що виражаються одним числом.
))так званими початковими точковими (точечними) оцінка, тобто оцінками, що виражаються одним числом.
2.У курсі мат.статистики доводиться,що середня вибіркова дає незміщену оцінку дійсної величини мат.сподівання. На відміну від неї вибіркова дисперсія дає зміцнену оцінку дійсної дисперсії досліджуваної кількісної ознаки. Незміщену оцінку дає величина

Це виправлена дисперсія. Оцінкою середнього квадратичного відділення(стандарту)є корінь з виправленої дисперсії.
Останні моменти збігаються. Якщо дослідні сформовані у вигляді інтервального ряду,в ролі варіант  ,виступають середини інтервалів (
,виступають середини інтервалів (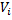 ).Продовжимо розглядати приклад на обробку міцності зразків при осьовому списку. Визначемо моменти статистичного розподілу для них, які ми згрупували в інтервальний ряд.
).Продовжимо розглядати приклад на обробку міцності зразків при осьовому списку. Визначемо моменти статистичного розподілу для них, які ми згрупували в інтервальний ряд.
Згадаємо ці дані:
| Розряди | 165-169 | 169-173 | 173-177 | 177-181 | 181-185 | 185-89 | |
Частоти, 
| 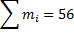
| ||||||
Відн. част., 
| 0.089 | 0.232 | 0.268 | 0.250 | 0.089 | 0.072 | |
Серед.інт., 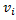
| 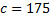
| ||||||
| -8 | -4 | ||||||

| -2 | -1 | |||||
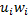
| -0.178 | -0.232 | 0.25 | 0.178 | 0.216 | 
| |
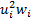
| 0.356 | 0.232 | 0.25 | 0.356 | 0.648 | 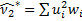 =1,842 =1,842
| |
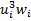
| -0.712 | -0.232 | 0.25 | 0.712 | 1.944 |  =1,962 =1,962
| |

| 1.424 | 0.232 | 0.25 | 1.424 | 8.832 |  =9,162 =9,162
|
|
|
|
У третьому рядку ми підрахували середні значення інтервалів. При цьому ми отримуємо знов дисперсійний ряд,але з меншим числом значень. Далі спрощення підрахувань виберемо новий початок рахунку. Це так званий хибний нуль (С). Його вибираємо у розряді з найвищої частотою і С=175- середина цього інтервалу. Введення цього нуля спрощує рахунки. Перейдемо до умовних варіантів:
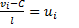 де
де
С-хибний нуль;
L - коефіцієнт масштабу (при однакових розрядах за l беремо довжину розряду). Це перетворення не міняє розподілу. Значенням 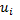 відповідають ті ж самі частоти
відповідають ті ж самі частоти 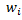 ,що і відповідні їм значення
,що і відповідні їм значення 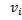 .
.
Начальні моменти які обмежені із значеннями  , мають назву умовних і позначають зверху знаком "^".І у зв’язку з введенням умовного нуля, розшукувані статистичні моменти будуть мати вигляд:
, мають назву умовних і позначають зверху знаком "^".І у зв’язку з введенням умовного нуля, розшукувані статистичні моменти будуть мати вигляд:
 =
= 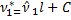
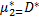 =(
=( 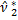 -(
-( 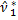 )
)  )
) 
 =(
=(  -3
-3  +2(
+2( 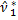 )
) 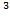 )
) 
 =(
=( 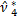 -4
-4 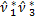 +6(
+6( 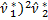 -3(
-3(  )
) 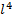
Підрахувавши 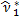 ,
, 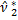 ,
,  ,
, 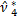 , занесемо все в таблицю.
, занесемо все в таблицю.
1.Визначаємо початковий момент першого порядку,тобто вибіркову середню:
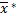 =
=  =0234·4+175=175,94
=0234·4+175=175,94
2.Визначимо:
-статистичний початковий момент другого порядку (умовний)
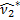 =1,842
=1,842
-статистичний центральний момент другого порядку,тобто вибіркова дисперсія:
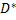 =
= 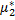 =(1,842-0,234
=(1,842-0,234  )·16=(1,842-0,055)·16=28,59.
)·16=(1,842-0,055)·16=28,59.
- виправлену диспресію:
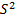 =
= 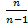
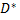 =
=  ·28,59 = 29,1.
·28,59 = 29,1.
-середне квадратичне відхилення (стандарт)
S =  =
= 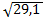 = 5,39.
= 5,39.
-відносну варіацію:
 =
= 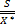 =
= 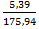 =0,031
=0,031
-коефіцієнт варіації:
 =
=  ·100%=0,031·100% ≈3,1%
·100%=0,031·100% ≈3,1%
3.Визначимо величини, які характеризують асиметрію та ексцес.
 =1,962
=1,962
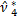 =9,162
=9,162
 =(1,962-3·0,234·1,842+2·0,234
=(1,962-3·0,234·1,842+2·0,234 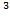 )·
)·  =44,6
=44,6
 =(9,162-4· 0,234·1,962+6·0,234·1,842-3·0,234
=(9,162-4· 0,234·1,962+6·0,234·1,842-3·0,234 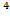 )·
)·  =2028
=2028
- статистична оцінка асиметрії:
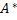 =
=  =
=  = 0,28
= 0,28
- статистична оцінка ексцесу:
 =
=  – 3 =
– 3 = 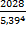 -3 =- 0,6.
-3 =- 0,6.
.
Аналізуючи статистичні моменти досліджуваної ознаки - міцності гірської породи на одноосьовий стиск-можна зробити такі висновки.
- середнє значення ознаки складає 175.94Мпа
- значення ознаки коливаються навколо свого середнього з невеликою варіацією, що складає 3,1 %.
- розподіл ознаки має невелику правобічну асиметрію ( ),його можна вважати майже симетричним.
),його можна вважати майже симетричним.
|
|
|
- значення ексцесу також близько до нуля. За виглядом гістограми можна припустити,що розподіл даної ознаки описується деякою функцією f(x), графік якої має максимум у точці x=175,94, крива майже симетрична щодо вертикальної прямої, проведеної через цю точку. Для прогнозу появи значень ознаки з тією чи іншої ймовірністю потрібно підібрати для функції f(x) аналітичний вираз. Існує ряд функцій,що задовільно описують розподіл деяких достатньо вивчених випадкових величин. Вони називаються теоретичними законами розподілу. Роздивляємось деякі з них.
§7.Деякі теоретичні закони розподілу.
7.1. Показниковий закон розподілу.
Така величина,як час безвідмовної роботи деякого механізму описується щільністю розподілу (диференціальною функцією),графік якої наведено на рисунку.
f(x)
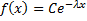
x
Видно,що це експонента,яка складає на проміжку (0;+  ). Для того,щоб ця функція описувала закон розподілу ймовірностей випадкової величини, вона повинна задовольняти умови
). Для того,щоб ця функція описувала закон розподілу ймовірностей випадкової величини, вона повинна задовольняти умови  1, тобто, у нас C
1, тобто, у нас C  dx = 1.
dx = 1.
Знайдемо значення С.
C  =
=  C
C 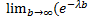 -
- 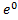 ) = -
) = -  (0-1) =
(0-1) = 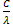 = 1,C=λ, звідси
= 1,C=λ, звідси 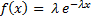 .
.
 - параметр розподілу,виражається,на основі статистичних даних. Насамперед визначимо теоретичні моменти даного розподілу і порівняємо їх з емпіричними:
- параметр розподілу,виражається,на основі статистичних даних. Насамперед визначимо теоретичні моменти даного розподілу і порівняємо їх з емпіричними:
1)початковий момент 1-го порядку, тобто мат.сподівання показникового розподілу
M(x)=  = λ
= λ  dx =
dx =  = λ
= λ 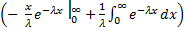 =λ
=λ 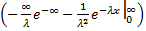 =
= 
M(x) =  .
.
2)центральний момент другого порядку,тобто,дисперсія
D(x) = λ 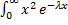 dx - (
dx - ( )
)  =
=  .
.
(довести самостійно)
3)середнє квадратичне відхилення:
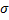 (x) =
(x) = 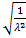 =
=  .
.
Як бачимо,параметр розподілу 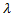 пов’язаний з числовими характеристиками ВВ. Крім того, можна побачити,що для показникового закону характерна рівність мат.сподівання і середньо квадратичного відхилення. Порівняємо теоретичні та емпіричні моменти 1-го порядку тобто
пов’язаний з числовими характеристиками ВВ. Крім того, можна побачити,що для показникового закону характерна рівність мат.сподівання і середньо квадратичного відхилення. Порівняємо теоретичні та емпіричні моменти 1-го порядку тобто
M(x) = 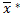
Так як 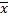
 =
= 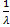 , то λ
, то λ 
Тобто,для знаходження параметра показникового розподілу досить мати середню вибіркову.
Приклад. Нехай відомі результати перевірки деякого прикладу на іспитовому стенді. Випробувано 100 зразків,вивчався час безвідмовної безупинної роботи приладу. Воно склало для 80 приладів менш 10 годин; для 10 приладів 10-20 годин; для 5- 20-30годин, для 5- 30-40 годин. Визначити ймовірність того,що час роботи приладу складає не менше 20 годин.
Збудуємо інтервальний ряд:
| Час безвідмовної роботи | 0-10 | 10-20 | 20-30 | 30-40 |
| Середній інтервал | ||||
| Кількість приладів(частота ознаки) | ||||
| Відносна частота | 0.8 | 0.1 | 0.05 | 0.05 |
Збудуємо гістограму відносних частот.
W
0,8
0,6
0,6
0,4
0,2
0 10 20 30 40 x
Дивлячись на неї, можна припустити, що дана кількість ознака-час безвідмовної роботи приладу – розподілена за показниковим законом.
Визначаємо емпіричні моменти розподілу:
середня вибіркова:
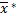 =5·0,8+15·0,1+25·0,05+35·0,05=8,5
=5·0,8+15·0,1+25·0,05+35·0,05=8,5
Вибіркова дисперсія
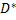 =5·0,8+225·0,1+625·0,05+1225·0,05-(8,5
=5·0,8+225·0,1+625·0,05+1225·0,05-(8,5  =62,75.
=62,75.
виправлена дисперсія
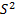 =
= 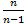 ·
· 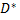 =
=  ·62,75 = 63,38
·62,75 = 63,38
Середнє квадратичне відхилення
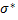 =
=  = 7,9.
= 7,9.
Бачимо,що мат.відхилення і середнє квадратичне відхилення близькі між собою. Це свідчить на користь показникового закону
F(x) = λ 
Виражаємо λ =  =
=  ≈ 0,117 ≈ 0,12
≈ 0,117 ≈ 0,12
Тепер. Маючи теоретичний закон розподілу, можна прогнозувати ймовірність появи того чи іншого значення цієї випадкової величини.
 = 0,091.
= 0,091.
Це ймовірність того, за час безвідмовної роботи приладу буде не менше 20 годин.
Показниковий закон відіграє велику роль в теорії машин та механізмів.
7.2.Нормальний закон розподілу.
Звернемось до прикладу про стиск зразків. Крива проведена через середини сторін прямокутників, у першому наближенні показує, який вигляд має диференціальна функція розподілу f(x). Крива має форму майже симетричну щодо вертикальної прямої x= 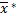 . Велика частина значень ВВ групується поблизу точки x=
. Велика частина значень ВВ групується поблизу точки x= 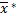 , що є точкою максимуму кривої.
, що є точкою максимуму кривої.
Багато ВВ мають подібну щільність розподілу ймовірностей. ЇЇ називають нормальним законом або законом Гауса
f(x) = 
f(x)
0 a x
Максимальна координата кривої →  відповідає точці х=
відповідає точці х=  . При віддаленні від т.
. При віддаленні від т.  щільність розподілу зменшується і при x→±
щільність розподілу зменшується і при x→± 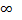 крива наближується до осі абсцис.
крива наближується до осі абсцис.
Знайдемо числові характеристики нормальної величини:
1)Математичне сподівання:
M(x)= 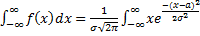 dx.
dx.
Замінимо 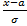 = t; dx=
= t; dx= 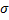 dt;
dt;
M(x)=  dt =
dt =  dt +
dt +  dt;
dt;
а)r w:top="850" w:right="850" w:bottom="850" w:left="1417" w:header="708" w:footer="708" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 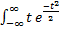 dt = -
dt = - 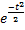 ⎥
⎥  = 0;
= 0;
б)Для обчислення другого інтеграла скористаємося тим що 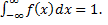 Для нормального розподілу ця умова буде:
Для нормального розподілу ця умова буде:
 dx=1,або в нових змінних
dx=1,або в нових змінних
 ; dt=
; dt= 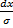 буде
буде 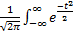 dt=1;
dt=1; 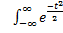 dt =
dt =  . Тоді
. Тоді
M(x)=  .
.
2)Аналогічно можна показати,що
D(x) = 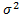 ;
;
середнє квадратичне відхилення 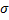 (x)=
(x)= 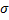 .
.
Отже параметрs w:ascii="Cambria Math" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="UK"/></w:rPr></m:ctrlPr></m:barPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="UK"/></w:rPr><m:t>a</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="850" w:right="850" w:bottom="850" w:left="1417" w:header="708" w:footer="708" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 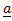 являє собою мат. сподівання і характеризує центр розподілу; параметр
являє собою мат. сподівання і характеризує центр розподілу; параметр  характеризує розсіювання випадкової величини щодо центра розподілу і обумовлює крутість кривої: чим більше
характеризує розсіювання випадкової величини щодо центра розподілу і обумовлює крутість кривої: чим більше 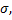 тим більше розсіювання,тим менше крутість кривої.
тим більше розсіювання,тим менше крутість кривої.
Можна показати що для нормальної випадкової величини центральний момент 3-го порядку дорівнює нулю (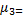 0), а центральний момент четвертого порядку дорівнює
0), а центральний момент четвертого порядку дорівнює  3
3  .
.
Це означає,що асиметрія й ексцес для нормального закону дорівнюють нулю:
(A=  =0; E=
=0; E=  – 3=0)
– 3=0)
Зауваження. Закон розподілу,що виражається диференціальною функцією
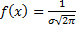

називається загальним нормальним. Для нього M(x)= 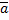 ,
,  . Часто при розв’язуванні задач переходять до нормальної величини:
. Часто при розв’язуванні задач переходять до нормальної величини:  . Для неї щільність розподілу буде:
. Для неї щільність розподілу буде:
f∘(t)= 
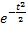
І називається нормованим нормальним розподілом. Мат.сподівання і середнє квадратичне відхилення для нормованої величини відповідно дорівнюють:
M(x)=0; 
Інтегральна функція нормального розподілу має вигляд:
А)для загального розподілу: 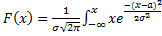 dx
dx
Б)для нормованого розподілу:F∘(t)=  dt.
dt.
Ці інтеграли не беруться в елементарних функціях, але для F∘ (t)існують таблиці. Також існують таблиці функцій Ф(t)= 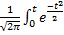 dt.
dt.
Це функція Лапласа.
Ймовірність улучення випадкової величини в заданий інтервал.
Згадаємо, що:
P(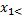 x
x 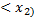 =
=  dx.
dx.
Зробимо заміну змінної:
t=  ; dx=
; dx= 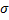 dt;
dt;  ;
; 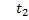 =
=  .
.
Тоді P( ) =
) =  dt=Ф (
dt=Ф ( )- Ф (
)- Ф (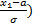 .
.
Ймовірність заданого відхиленння.
Правило "3-х сигм".
Знайдемо ймовірність того що відхилення нормальної випадкової величини Х від її мат.сподівання  не перевищує величини
не перевищує величини 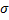 . Тобто знайдемо ймовірність події
. Тобто знайдемо ймовірність події
P(
Згідно останній формулі: P(│ 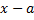 │
│  ) -
) -  ) =
) = 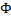 (
(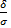 ) - Ф(
) - Ф(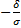 ) = 2
) = 2 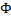 (
(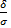 ) так як функція Ф(t) непарна.
) так як функція Ф(t) непарна.
- Проаналізуємо такі випадки:
- 1. Нехай 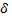 =
= 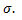 Тоді P(│
Тоді P(│ 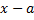 │
│  2
2 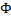 (
(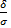 )= 2Ф (1)=0,68. Тут значення Ф(1)=0.34- знайдені по таблиці.
)= 2Ф (1)=0,68. Тут значення Ф(1)=0.34- знайдені по таблиці.
- 2. Нехай 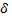 =
= 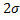 . Тоді P(│
. Тоді P(│ 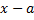 │
│ 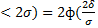 ) = 2ф(2) = 0,478·2 =0,95.
) = 2ф(2) = 0,478·2 =0,95.
- 3.Нехай 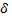 =
= 
 Тоді P(│
Тоді P(│ 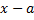 │
│  )=2ф(3)=0,997.
)=2ф(3)=0,997.
Бачимо що з ймовірністю 0.997,тобто з практичноювірогідністю,значення нормальної величини потрапляють в інтервал:
 .
.
Це" Правило 3-х сигм "За його допомогою можна судити про те,чи є дана випадкова величина розподілена за нормальним законом чи ні. Таким чином підставою для вибору гіпотези є виконання умов:
1).99,7% значення випадкової величини належать інтервалу:
 .
.
2)асиметрія й ексцес близькі до нуля (A 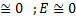 ).
).
Звернемось до нашого прикладу з осьовим стиском. Бачимо,що крива,що вирівнює гістограму, має такий же вигляд, як і нормальна щільність розподілу. Асиметрія А=0.28 і ексцес Е=- 0.6 близькі до нуля.
Перевіримо виконання правила «3-х сигм».

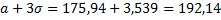
159,74 
Дійсно,  =165 і
=165 і  =189 укладаються в цей інтервал. Тому в першому наближенні ми можемо висунути гіпотезу про те,що значення досліджуваної кількісної ознаки - міцності на стиск гірської породи – підпорядковується нормальному закону розподілу. Визначаємо параметри цього розподілу на основі дослідних даних. Використовуємо метод моментів. Дорівнюємо початкові статистичний і теоретичний момент и розподілу.
=189 укладаються в цей інтервал. Тому в першому наближенні ми можемо висунути гіпотезу про те,що значення досліджуваної кількісної ознаки - міцності на стиск гірської породи – підпорядковується нормальному закону розподілу. Визначаємо параметри цього розподілу на основі дослідних даних. Використовуємо метод моментів. Дорівнюємо початкові статистичний і теоретичний момент и розподілу.
M(x) =  Для нормального закону M(x)=
Для нормального закону M(x)=  . Тому
. Тому 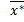 =
=  =175,94. Для знаходження ще одного невідомого параметру (
=175,94. Для знаходження ще одного невідомого параметру (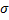 ) дорівнюємо центральні моменти другого порядку: D(x)=
) дорівнюємо центральні моменти другого порядку: D(x)= 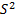
Для нормального закону D(x)=  тому
тому 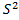 =
= 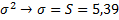 .
.
Отримаємо тезу про теоретичний закон розподілу в першому наближенні:
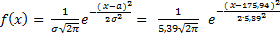 .
.
У відповідальних рахунках перевірка статистичної гіпотези потрібна більш ретельна за так званими критеріями згоди.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1736; Нарушение авторских прав?; Мы поможем в написании вашей работы!