Функціонал оцінювання 3 страница

Розв’язання.

а) Скориставшись тим, що

,

отримуємо систему рівнянь:

.

Розв’язавши цю систему рівнянь, отримуємо, що x ₁ = 0,5, x ₂ = 0,5,

.

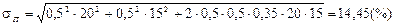б) Скориставшись тим, що

,

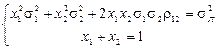отримуємо систему рівнянь

.

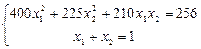Ця система рівнянь зводиться до квадратного рівняння:

415 x ₁² – 240 x ₁ – 31 = 0,

яке має корені x ¢ = – 0,109 та x ¢¢ = 0,687. Оскільки x ¢ < 0, то в ПЦП частка ЦП виду A ₁ становить x ₁ = x ¢¢ = 0,687, виду A ₂ — x ₂ = 1 –– x ¢¢ = 0,313.

Сподівана норма прибутку отриманого ПЦП становить

m_П = x ₁ m ₁ + x ₂ m ₂ = 0,69 × 60 = 0,31 × 40 = 53,84(%).

Портфель з багатьох видів цінних паперів

Перейдемо тепер до загального випадку, коли до складу ПЦП залучено N (N > 2) різних акцій.

Розглянемо, наприклад, три акції, що мають норми прибутку відповідно 15%, 10%, 5%, середньоквадратичні відхилення 10%, 7%, 3% і коефіцієнти кореляції r₂₃ = – 0,2; r₁₂ = – 0,4; r₁₃ = + 0,6. У системі координат m_П – s _П (норма прибутку — ризик, рис.5) побудуємо точки А ₁, А ₂, А ₃, що відповідають однорідним ПЦП, сформованим з відповідних акцій. На цьому ж рисунку побудуємо лінії (дуги), що відповідають ПЦП, сформованому з двох видів акцій (ÈА₃А₁; ÈА₃А₂; ÈА₂А₁).

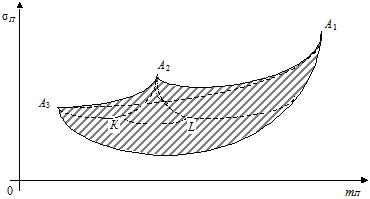
Рис. 4.5. Множина допустимих портфелів цінних паперів

Точкам К Î È А ₃ А ₂ та L Î È А ₂ А ₁відповідають певні ПЦП, cформовані з двох (відповідно А ₃, А ₂та А ₂, А ₁) видів акцій. Для цих портфелів можна розрахувати норми прибутку і ризики. Вважатимемо тепер, що кожний з цих портфелів є певного виду «цінним папером» відповідно К та L. А тому, в свою чергу, можна сформувати новий ПЦП для ЦП К та L. Такі ПЦП вже будуть включати по три акції (А ₁, А ₂, А ₃) і їм відповідає дуга È КL.

Міркуючи таким чином, приходимо до висновку, що кожна точка, яка належить до заштрихованої області (рис. 4.5), відповідає деякому ПЦП, сформованому з трьох видів акцій.

Допустимою множиною ПЦП називається область, точки якої характеризують ступінь ризику та норму прибутку портфеля за всіх можливих часток окремих акцій в портфелі (на рис. 4.5 — це область, обмежена жирною лінією).

Особливістю дуги È О*А ₁, яка належить допустимій множині, є те, що для будь-якої точки цієї дуги не можна вказати іншої точки допустимої області, для якої ПЦП був би кращим.

Ефективною множиною ПЦП називаються ті портфелі, що відповідають точкам дуги È О*А ₁. Тобто ефективним портфелем вважається такий, для якого в допустимій множині ПЦП не можна вказати іншого портфеля:

· з тим же значенням величини сподіваної норми прибутку і меншим ступенем ризику;

· з тим же значенням величини ризику і більшим значенням сподіваної норми прибутку.

Очевидно, що для ПЦП, складених з двох акцій, допустима множина збігається з множиною ефективних портфелів, і вони складають дугу È О*А ₁ (рис. 4.4).

Розглянемо тепер загальний випадок побудови ПЦП, сформованого з N ЦП. Як і раніше, позначимо через R_k, m_k = M (R_k), s _k — відповідно норму прибутку, сподівану норму прибутку та ризик k -го ЦП, k = 1,..., N; через r _kj — коефіцієнт кореляції між k -тим та j -тим видом ЦП.

Задача збереження капіталу

Сутність її полягає у виборі такої структури ПЦП, щоб ризик цього портфеля був мінімальним. Формальна постановка цієї задачі така:

;

Розв’язку задачі відповідає точка О^* на рис. 4.6. Метод знаходження структури ПЦП, що задовольняє умову поставленої задачі, базується на побудові та знаходженні точки мінімуму відповідної функції Лагранжа, яке, в свою чергу, зводиться до розв’язання наступної системи лінійних алгебраїчних рівнянь [4]:

(4.9)

Тут l — додаткова змінна (невідома величина) поява якої спричинена використанням методу Лагранжа.

Слід мати на увазі, що метод Лагранжа, запропонований для розв’язання поставленої задачі, не враховує обмежень щодо невід’ємності величин x_k, тобто що x_k ³ 0; k = 1,..., N. А тому розв’язок системи (4.9) необхідно проаналізувати з цієї позиції.

Позначимо через Х^* = { x ₁^*; x ₂^*;…; x_N ^*} розв’язок системи (4.9). Якщо всі компоненти вектора Х ^* є додатними (x_k ^* > 0, k = 1,..., N) то цей вектор описує структуру оптимального ПЦП, що відповідає точці О^* (рис. 4.6).

Якщо серед компонент Х^* виявляться від’ємні, то в шуканий ПЦП не включається той ЦП, частка якого є від’ємною і найменшою серед отриманих від’ємних часток. Після вилучення цього ЦП знову розраховується структура оптимального ПЦП, складеного з (N – 1) ЦП. Процес вилучення такого роду «несприятливих» ЦП продовжується до тих пір, поки частки всіх ЦП, включених у портфель, не стануть позитивними.

Рис. 4.6. Геометрична інтерпретація задач щодо формування різних видів ПЦП

Приклад 8. Сподівані норми прибутку акцій виду A ₁, A ₂, A ₃та A ₄ становлять відповідно 60%, 50%, 40% та 70%. Ризики цих акцій становлять 40%, 30%, 25% та 50%. Тісноту зв’язку між нормами прибутку цих акцій відображають коефіцієнти кореляції r₁₂ = 0.2; r₁₃ = – 0,3; r₂₃ = – 0,5; r₁₄ = 0,9; r₂₄ = 0,7; r₃₄ = – 0,3.

Необхідно сформувати з цих акцій ПЦП, що має мінімальний ризик. Оцінити його сподівану норму прибутку та його ризик.

Розв’язання. Згідно з умовою задачі

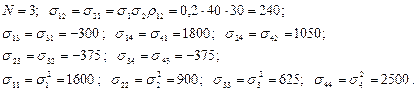
Згідно з (4.9) отримуємо систему рівнянь:

.

Розв’язавши отриману систему рівнянь, знаходимо: х ₁ = 2,412; х ₂ = 1,768; х ₃ = – 0,402; х ₄ = – 2,778. Оскільки х ₄ = – 2,778 — є найменшим від’ємним числом, то надалі акцію виду А ₄ в ПЦП не включаємо. Для акцій виду А ₁, А ₂ та А ₃ складаємо нову систему рівнянь:

.

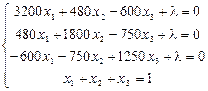Згідно з останньою системою рівнянь отримуємо, що х ₁ = 0,1392; х ₂ = 0,3453; х ₃ = 0,5155.

Тоді величина сподіваної норми прибутку ПЦП

m_П^* = x ₁ m ₁ + x ₂ m ₂ + x ₃ m ₃ = 46,237,

а мінімальна величина ризику серед усіх ПЦП, сформованих з ЦП виду А ₁, А ₂ та А ₃, становить

Зауваження 2. Якщо ввести позначення

; ; ,

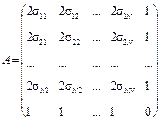то систему рівнянь (4.9) можна записати у матричному вигляді:

.

Тоді розв’язок системи (4.9) знаходиться згідно з формулою:

.

Задача одержання бажаного (фіксованого) прибутку

Сутність задачі полягає у виборі такої структури ПЦП, щоб сподівана норма прибутку цього портфеля була не меншою від зафіксованого рівня m_c (m_c = const) і його ризик при цьому був мінімальним. Формально цю задачу запишемо у вигляді таких спів­відношень:

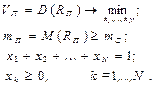
Розв’язку задачі одержання прибутку відповідає точка «К» на рис.3.6. Для знаходження структури ПЦП, що задовольняє умовам поставленої задачі, як і раніше, скористаємось методом Лагранжа [4], який зводиться до знаходження розв’язку системи лінійних алгебраїчних рівнянь:

(4.10)

де l₁,l₂ — додаткові змінні (невідомі величини), поява яких спричинена використанням методу Лагранжа.

Приклад 9. З акцій виду А ₁, А ₂ та А ₃, описаних в умові прикладу 8, сформувати ПЦП, сподівана норма прибутку якого становила б m_c = 50% і при цьому ризик портфеля був би мінімальним. Обчислити величину його ризику.

Розв’язання. Згідно з (4.10) отримуємо систему рівнянь:

.

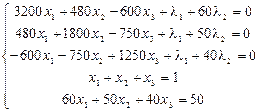Розв’язавши цю систему рівнянь, отримуємо, що х ₁= 0,402; х ₂ = 0,196; х ₃ = 0,402.

Сподівана норма прибутку сформованого ПЦП

m_П = 0,402 × 60 + 0,196 × 50 + 0,402 × 40 = 50 = m_c,

а його ризик

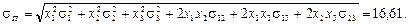
Як бачимо, що якби ПЦП був сформований лише з акцій виду А ₂, то його сподівана норма прибутку була б рівною m_c = 50%, але ризик його в такому випадку становив би s _П = 30%, тобто був би більшим майже в два рази.

[1] “ Пасивне” економічне середовище характеризують перша, друга, третя та четверта інформаційні ситуації, оскільки згідно з на­веденою вище класифікацією стани економічного середовища в полі цих інформаційних ситуацій реалізуються відповідно до заданого або гіпотетичного закону розподілу ймовірностей.

[2] Символ “:” в математичних викладках є еквівалентом слів “для якого”.

Дата добавления: 2014-12-23