Деякі відомості з диференціальної геометрії

Способі ЗАДАННЯ руху

Прискорення точки при натуральному

Лекція 13

1. Кривизна кривої. Розглянемо просторову криву (рис. 13.1). Проведемо дотичні у двох близьких точках кривої. Орт дотичної у точці 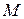позначимо через 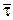, а у точці 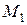через 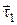. Перенесемо вектор 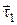паралельно у точку 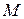. Кут між напрямами дотичних у двох близьких точках кривої називається кутом суміжності: .

Позначимо дугу 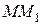через .

Кривизною кривої у даній точці М називається границя відношення кутасуміжності до абсолютного значення елемента дуги , коли точка 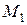необмежено наближається до точки :

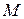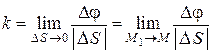. (13.1)

Кривизна кола в усіх її точках однакова. Кривизна прямої дорівнює нулю.

У загальному випадку кривизна кривої не є сталою величиною і змінюється від точки до точки кривої.

Величина, обернена кривизні кривої, називається радіусом кривизни кривої вданій точці

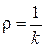. (13.2)

2. Натуральні осі. Проведемо площину через дотичну до кривої у точці 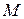і пряму, паралельну дотичній в точці 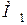, що необмежено наближається до точки 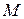,тобто через вектори 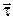і 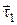, прикладені у точці 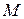(рис. 13.1).

Граничне положення цієї площини при наближенні точки 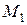до точки 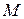називається стичною площиною до кривої в даній точці.

Для плоскої кривої стична площина це площина, в якій розташована крива.

Площина, що проведена через точку 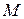кривої перпендикулярно дотичній, називається нормальною площиною.

Нормаль до дотичної, що лежить у стичній площині, називається головною нормаллю. Орт головної нормалі позначимо через 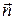. Він спрямований у бік угнутості кривої (рис. 13.2).

Лінія, що проведена через точку М, перпендикулярно стичній площині, називається бінормаллю.

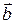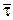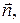
Площина, в якій розташовані дотична і бінормаль, називається спрямною площиною. Орт бінормалі направлений так, щоб вектори , 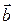утворили праву систему ортогональних осей.

Тригранник, що утворений стичною, нормальною і спрямною координатними площинами, називається натуральним тригранником.

Три взаємно перпендикулярні осі – дотична, головна нормаль і бінормаль називаються натуральними координатними осями (рис. 13.2).

Початок натуральних осей завжди знаходиться у точці 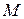кривої і при русі точки вздовж кривої натуральні осі переміщуються разом з точкою, змінюючи при цьому свій напрям.

3. Похідну від орта дотичної 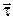за дуговою координатою 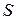визначаємо на основі другої основної теореми диференціальної геометрії:

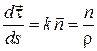. (13.3)

Пояснимо формулу (13.3). За визначенням похідної витікає, що

.

Вектор 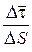лежить у площині 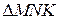(рис. 13.1). Граничне положення цієї площини визначає стичну площину в даній точці 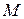.Коли 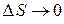, то кут 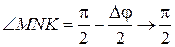. Отже, вектор 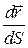спрямований у напрямі головної нормалі з ортом 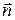, тобто: = .

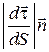З рівнобічного 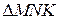(рис. 13.1): 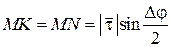, де . Тоді:

.

Помножимо чисельник і знаменник правої частини цієї формули на 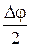і після тотожніх перетворень, одержимо:

,

де, як відомо, перший множник дорівнює одиниці, а другий – кривизн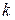і кривої , – радіус кривизни цієї кривої.

Підставляючи отриманий вираз 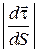у (13.3), остаточно отримаємо:

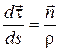. (13.4)

13.2. Теорема про прискорення точки при натуральному способі задання руху:

Дата добавления: 2014-12-25