Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

Практическое занятие № 19

Тема занятия « Логарифмическое дифференцирование. Производные высших порядков. Функции заданные неявно и параметрически и их дифференцирование »

Цель занятия: Формирование умений и навыков нахождения производных неявно заданных и параметрически заданных функций, применения логарифмического дифференцирования.

Организационная форма занятия: практикум-тренинг.

Компетенции, формируемые на занятии: ОК-1.

Формирование у будущих специалистов этой компетенций на занятии предполагает обучение студентов

- анализировать ситуации и делать выводы;

- видеть проблемы в традиционных ситуациях;

- абстрагировать содержание и выделять существенное;

- применение основных понятий, идей и методов математического анализа для решения базовых задач.

1. Логарифмическое дифференцирование.

2. Производные высших порядков.

3. Неявно заданные функции и их дифференцирование.

4. Нахождение производной параметрически заданной функции.

Для подготовки к занятию дома

1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

6. Подготовьтесь к самостоятельной работе №7 по теме «Производная функции», просмотрев решение основных типов задач, предложенных в примерном варианте самостоятельной работы.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

3. Решите, предложенный преподавателем, вариант самостоятельной работы №7 по теме «Производная функции» и сдайте выполненную работу на проверку.

Дома

1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

2. В тетради для индивидуальных домашних заданий закончите выполнение ИДЗ №5 по теме «Вычисление производных» в соответствии с Вашим вариантом. Решите задания 4 и 5. В задании 4 найдите производную функции с помощью логарифмического дифференцирования; в задании 5 найдите производную 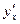для функции заданной неявно. Сдайте тетрадь на проверку преподавателю.

3. Подготовьтесь к самостоятельной работе №8 по теме «Дифференцирование неявно заданных и параметрически заданных функций», примерный вариант самостоятельной работы вы можете найти в программе дисциплины.

Рекомендуемая литература

[1] глава 8 пп. 8.4. - 8.5.

[2] глава VII § 1.

[3] глава 6 § 29.

[4] часть II занятия 25 – 27.

[5] глава 2 § 2.1.

[6] глава 5 §§ 9 – 11.

[7] глава V §§ 9 – 11.

[8] глава 5 §§ 9 – 11.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. С помощью логарифмического дифференцирования найдите производные следующих функций:

а) 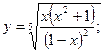б)

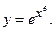
Решение. а) Производную функции найдем по следующему плану:

1) Прологарифмируем данную функцию:

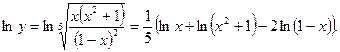
2) Найдем производную от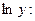

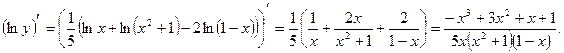
Определим производную данной функции

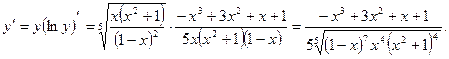
б) Производную функции с помощью логарифмического дифференцирования находим по указанному плану:

1)

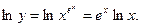
2)

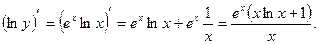
3) .

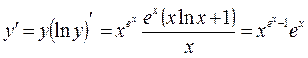2. Для функции 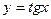найдите производные второго и третьего порядков.

Решение. По определению производных высших порядков имеем:

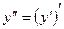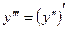и , т.е. производная второго порядка есть производная от производной первого порядка, а производная 3-го порядка есть производная от производной 2-го порядка. Поэтому последовательно находим:

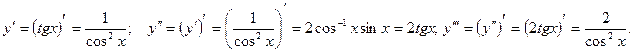
3. Для данных неявных функций найдите производные первого порядка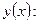

а) 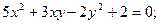б)

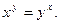
Решение. а) Дифференцируем по 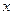обе части равенства, считая, что 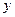есть функция от 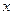, получим:

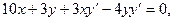отсюда 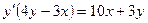, или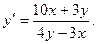

б) Логарифмируем обе части данного уравнения, затем дифференцируем по 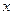, рассматривая 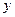как функцию от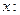

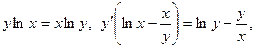отсюда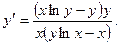

4. Для функции, заданной параметрически, найдите производную: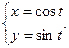

Решение. Учитывая, что 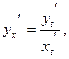найдем 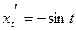и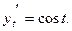

Тогда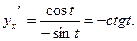

Теоретические задания

для развития и контроля владения компетенциями

1. Запишите формулу логарифмического дифференцирования.

2. Когда применяется формула логарифмического дифференцирования?

3. Расскажите о дифференцировании показательно-степенной функции.

4. Дайте определение производной второго порядка, производной n-го порядка.

5. Дайте определение неявного задания функции. Приведите примеры.

6. Как от неявного задания перейти к явному заданию функции? Всегда ли это можно сделать. Приведите примеры.

7. Как проводят дифференцирование неявной функции?

8. Расскажите о нахождении производных высших порядков от неявно заданных функций.

9. Дайте определение параметрически заданной функции. Приведите примеры.

10. Расскажите как от параметрического задания функции перейти к явному заданию функции.

11. Запишите формулы для нахождения производных первого и второго порядков от параметрически заданной функции.

Практические задания

Дата добавления: 2014-12-26