Движение точки с позиций теоретической механики

КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

Задача кинематики - описание движения среды независимо от внешних условий, которые инициируют и поддерживают движение. Т.к. сплошная среда представляет собой непрерывную совокупность точек, то чтобы описать её движение, необходимо описать движение всех точек. Поэтому вернёмся к некоторым понятиям теоретической механики, изучающей движение точки.

Траектория движущейся точки. Движение материальной точки мы рассматриваем в теоретической механике. В этом случае, для описания полного движения точки необходимо знать уравнение её движения т.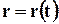е. , где 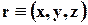- радиус-вектор точки. Чтобы найти скорость точки надо взять производную от правой части уравнения движения.

Рассмотрим движение точки в некоторой определённой системе прямоугольных и прямолинейных координат Oxyz, которую условимся называть неподвижной.

Кривая, описываемая последовательными положениями движущейся точки, называется траекторией.

Аналитически движение точки определено, если заданы её координаты x, y, z, как непрерывные функции времени t:

x = j₁ (t); y = j₂(t); z = j₃(t).

Эти уравнения определяют положение движущейся точки в каждый момент времени t и представляют в параметрической форме уравнение траектории. Если на траектории выбрать точку М₀, от которой отсчитывать длину дуги s траектории до движущейся точки М, то движение М определяется законом изменения s, как функции времени t:

s = s (t).

Перемещение. Скорость. Пусть М и М¢ - положения движущейся точки, отвечающие соответственно моментам t и t + Dt. Вектор 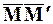называется перемещением точки за промежуток времени Dt. Этот вектор с началом в точке М представляет собой хорду, стягивающую положения движущейся точки в моменты t и t + Dt.

Перемещение 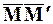разделим на Dt; вектор

называется средней скоростью точки М за промежуток времени Dt.

Средняя скорость есть вектор, приложенный в точке М и имеющий то же направление, что и перемещение .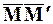

Предел средней скорости, когда Dt стремится к 0, называется скоростью точки М в момент t и обычно обозначается

.

В пределе направление хорды совпадает с направлением касательной к траектории; поэтому скорость u точки М представляет собой вектор, приложенный в точке М и направленный по касательной к траектории в сторону движения.

Положение точки М можно определить вектором , выходящим из начала координат О. Перемещение 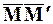за промежуток времени Dt равно приращению вектора :

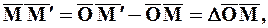
откуда

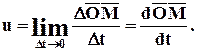
Таким образом, скорость движущейся точки равна производной по времени от радиуса-вектора движущейся точки и представляет собой вектор, приложенный в движущейся точке.

Проекции скорости на оси координат. Пусть x, y, z координаты точки М, а x + Dx, y +Dy, z +Dz - координаты точки . Проекции перемещения 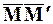на оси координат будут соответственно равны Dx, Dy, Dz; проекции средней скорости w будут

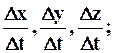
отсюда проекции истинной скорости u на оси координат Oxyz будут пределами предыдущих выражений при Dt® 0, или

Теорема. Проекции скорости на прямоугольные оси равны первым производным по времени от соответствующих координат движущейся точки.

Так как оси Oxyz ортогональны, величина скорости определится через проекции формулой:

.

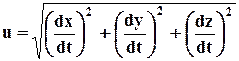Если через s обозначить длину дуги траектории, отсчитываемой от неподвижной точки, то

.

Следовательно, алгебраическая величина скорости будет определяться формулой

.

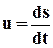При этом, если u положительна, то скорость направлена в сторону возрастающих значений s. Движение называется равномерным, если величина скорости постоянна. Тогда

Допустим, что s₀ есть значение s для начального момента времени t = 0; тогда, интегрируя предыдущее выражение, получаем: s = s₀ + at.

То есть, в равномерном движении пройденные пути пропорциональны времени. Величина скорости равна пути, пройденному в равномерном движении за единицу времени.

Теорема о проекции скорости. Возьмём ось х за траекторию движения (если движение прямолинейное). Значит s = х, и уравнение движения имеет вид: x = f(t). Алгебраическая величина скорости точки, движущейся по оси х, представляется формулой

v = dx/dt = f¢(t).

Но, при движении точки в пространстве, dx/dt есть проекция её скорости на ось х; в то же время эта величина равна скорости ортогональной проекции М₁ точки М на ось х, так как х есть абсцисса точки М₁.

Следовательно, если спроектировать на неподвижную ось движущуюся точку и её скорость, то проекция скорости будет равна скорости проекции.

Дата добавления: 2014-12-26