
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы криптоанализа ассиметричных криптосистем
|
|
|
|
4.1. Методы, основанные на алгоритмах разложения на множители
В этом пункте рассматриваются методы «взлома» основанные на решении задачи факторизации (IFP). Очевидно, что зная разложение (1.9) можно решить задачу RSA путем вычисления обратной функции. Если это разложение неизвестно, то требуется определить такой алгоритм, который позволил бы решить задачу RSA за полиномиальное время, т.е.
 ,
,
где 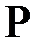 - класс задач, решаемых за полиномиальное время детерминированной машиной Тьюринга,
- класс задач, решаемых за полиномиальное время детерминированной машиной Тьюринга,  - символ операции импликации.
- символ операции импликации.
Самые эффективные алгоритмы факторизации можно разделить на две группы [3,7,8]:
1. Алгоритмы, время выполнения которых зависит главным образом от размера 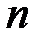 . К таким алгоритмам относятся: алгоритм Ферма, метод Лемана, метод квадратичных форм Шенкса, метод цепных дробей, метод решета, метод решета числового поля.
. К таким алгоритмам относятся: алгоритм Ферма, метод Лемана, метод квадратичных форм Шенкса, метод цепных дробей, метод решета, метод решета числового поля.
2. Алгоритмы, время выполнения которых зависит главным образом от размера множителя  . При выполнении условия
. При выполнении условия  эффективными алгоритмами факторизации являются:
эффективными алгоритмами факторизации являются:  -метод Полларда,
-метод Полларда,  -метод Полларда, метод Ленстры, метод пробного деления.
-метод Полларда, метод Ленстры, метод пробного деления.
Кроме того, алгоритмы факторизации можно разделить на детерминированные и недетерминированные, условные и безусловные. Условными являются те алгоритмы, в которых на раскладываемое число  налагаются дополнительные условия, например,
налагаются дополнительные условия, например,  - нечестное составное число длиной
- нечестное составное число длиной  бит,
бит,  и
и  - простые числа длиной
- простые числа длиной  .
.
Рассмотрим некоторые из перечисленных методов.
Алгоритм факторизации Ферма. Для того, чтобы было сложнее факторизовать 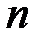 и решить задачу RSA,
и решить задачу RSA,  и
и  выбираются одинаковой битовой длины. Однако, если
выбираются одинаковой битовой длины. Однако, если  и
и  слишком близки друг к другу, то становится возможным достаточно быстро найти их. Пусть
слишком близки друг к другу, то становится возможным достаточно быстро найти их. Пусть  , где
, где  и оба нечетные, тогда положив
и оба нечетные, тогда положив  и
и  , получаем, что
, получаем, что 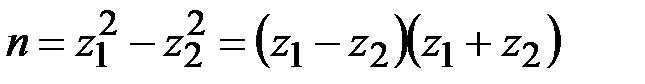 или
или  . На этой идее основан алгоритм Ферма. При известном нечетном целом
. На этой идее основан алгоритм Ферма. При известном нечетном целом 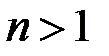 алгоритм находит наибольший множитель
алгоритм находит наибольший множитель  . Существо алгоритма в следующем.
. Существо алгоритма в следующем.
|
|
|
1. Вводится 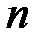 и
и 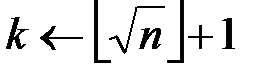 ,
, 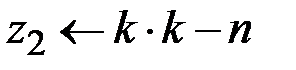 ,
, 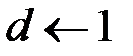 .
.
2. Если  , то требуется перейти сразу к 4 шагу алгоритма, иначе
, то требуется перейти сразу к 4 шагу алгоритма, иначе 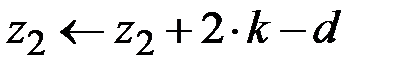 и
и  .
.
3. 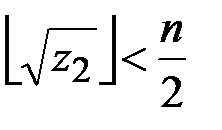 , то требуется перейти ко второму шагу алгоритма, иначе задача нахождения множителей считается не решаемой и алгоритм заканчивается.
, то требуется перейти ко второму шагу алгоритма, иначе задача нахождения множителей считается не решаемой и алгоритм заканчивается.
4. 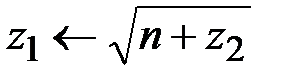 ,
, 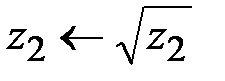 . Определяются значения нетривиальных множителей
. Определяются значения нетривиальных множителей 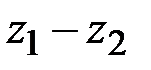 и
и 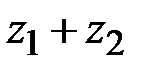 числа
числа 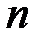 .
.
Алгоритм Ферма эффективен для небольших 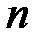 . Количество циклов
. Количество циклов  , необходимых для достижения результата оценивается неравенством [8]
, необходимых для достижения результата оценивается неравенством [8]
 .
.
Следовательно, для обеспечения стойкости RSA необходимо, чтобы разность 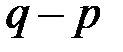 была велика.
была велика.
 -метод Полларда. Простые числа
-метод Полларда. Простые числа  и
и  в RSA необходимо выбирать, исходя из тех соображений, чтобы
в RSA необходимо выбирать, исходя из тех соображений, чтобы 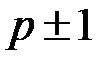 ,
, 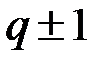 имели по крайней мере один простой делитель, больший
имели по крайней мере один простой делитель, больший 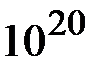 [8], в противном случае
[8], в противном случае 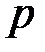 можно эффективно найти, используя
можно эффективно найти, используя  -метод Полларда (или
-метод Полларда (или  -метод Вильямса).
-метод Вильямса).
Пусть  составное число. Рассмотрим алгоритм по шагам.
составное число. Рассмотрим алгоритм по шагам.
1. Шаг инициализации. Случайно выбирается  , где
, где 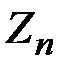 - класс остатков по модулю
- класс остатков по модулю  :
:  ,
,  - множество целых чисел. Выбирается положительное целое число
- множество целых чисел. Выбирается положительное целое число 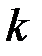 , которое делилось бы на множество простых степеней, например,
, которое делилось бы на множество простых степеней, например, 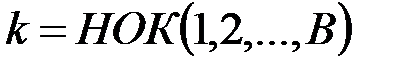 , для соответствующей границы
, для соответствующей границы  . Чем больше
. Чем больше 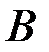 , тем более вероятно, что найдется множитель, но тем дольше будет работать алгоритм.
, тем более вероятно, что найдется множитель, но тем дольше будет работать алгоритм.
2. Шаг возведения в степень. Вычисляется  .
.
3. Шаг вычисления НОД. Вычисляется 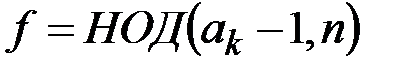 .
.
4. Шаг проверки условия 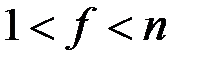 . Если условие выполняется, то
. Если условие выполняется, то  - нетривиальный делитель
- нетривиальный делитель  и алгоритм заканчивается. Один из множителей
и алгоритм заканчивается. Один из множителей  найден. Если условие не выполняется, то
найден. Если условие не выполняется, то  - тривиальный делитель. Тогда требуется перейти к шагу 2, выбрав новое
- тривиальный делитель. Тогда требуется перейти к шагу 2, выбрав новое  и/или новое
и/или новое  .
.
Алгоритм эффективен только при малом 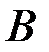 . Сложность алгоритма составляет
. Сложность алгоритма составляет 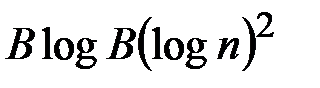 .
.
Пример. Используем  -метод Полларда для факторизации
-метод Полларда для факторизации 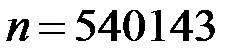 . Выберем
. Выберем  , отсюда
, отсюда  . Выберем
. Выберем 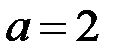 . Тогда
. Тогда
 .
.
Выполняется условие  , т.е. один из множителей
, т.е. один из множителей  найден. Действительно,
найден. Действительно, 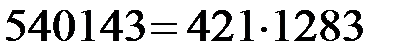 .
.
|
|
|
4.2. Методы, основанные на алгоритмах вычисления дискретного логарифма
Рассматриваемые в этом пункте методы основаны на решении задачи дискретного логарифмирования (DPL). Если существует возможность решить задачу DPL за полиномиальное время, то тогда за полиномиальное время можно «взломать» и криптосистему, основанную на задаче DPL, например криптосистему Эль Гамаля:
 .
.
Существуют три принципиально различных класса алгоритмов, которые используются для вычисления дискретного логарифма [3,6,8].
1. Алгоритмы, которые работают с произвольными группами. Они не используют никаких специальных свойств групп. К этому классу относятся: алгоритм больших и малых шагов (алгоритм Шенкса),  -метод Полларда (аналог
-метод Полларда (аналог  -метода факторизации Полларда),
-метода факторизации Полларда),  -метод (метод «кенгуру»).
-метод (метод «кенгуру»).
2. Алгоритмы, работающие с конечными группами, порядок которых не имеет больших простых делителей; точнее сказать, с группами, порядок которых является гладким числом. К этому классу принадлежит хорошо известный алгоритм Сильвера-Полига-Хеллмана, основанный на теореме об остатках.
3. Алгоритмы, которые используют метод представления элементов группы в виде произведения элементов, принадлежащих множеству небольшой мощности. Типичным представителем этого класса являются алгоритмы исчисления порядка Адлемана и NFS алгоритм Говарда.
Рассмотрим алгоритмы каждого класса.
Метод малых и больших шагов. Этот метод впервые был описан Д. Шенксом в 1973 году. Метод является одним из первых, который показал, что решить задачу DPL можно быстрее, чем методом полного перебора. Метод Шенкса широко известен и под другим названием – «шаг младенца, шаг великана». Существо метода заключается в следующем.
Выбирается два целых числа 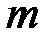 и
и  , такие что
, такие что 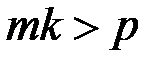 . Затем вычисляются два ряда чисел
. Затем вычисляются два ряда чисел
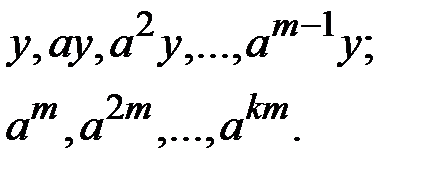
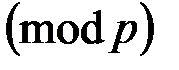 (4.1)
(4.1)
Из равенства
 ,
,
определяются числа  и
и  , и затем определяется
, и затем определяется
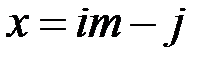 . (4.2)
. (4.2)
Докажем, что (4.2) справедливо. Действительно,
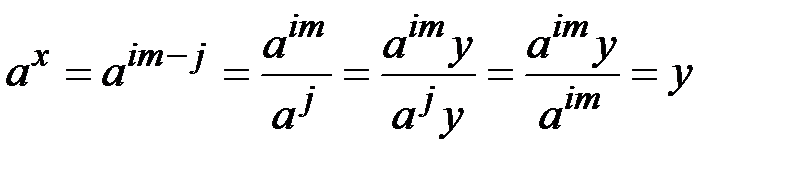 .
. 
В [6] приведено доказательство существования чисел  и
и  .
.
Метод больших и малых шагов назван так по следующей причине. В (4.1) первый числовой ряд увеличивается медленнее второго, так как степень числа  увеличивается на единицу (малый шаг), а во втором числом ряду степень увеличивается на
увеличивается на единицу (малый шаг), а во втором числом ряду степень увеличивается на  (большой шаг).
(большой шаг).
|
|
|
Пример. Требуется найти решение уравнения  . Выберем
. Выберем 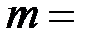 6 и
6 и  4 (24>23). Вычислим два ряда чисел
4 (24>23). Вычислим два ряда чисел

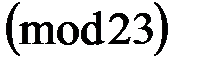
Таким образом, из равенства  получаем
получаем  и
и 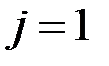 . Тогда
. Тогда  .
.
Алгоритм исчисления порядка. Алгоритм исчисления порядка известен с начала двадцатого века, однако только в 1979 году Адлеман показал, что его можно использовать для решения задачи DPL.
Для описания алгоритма введем некоторые понятия [6].
Определение 4.1. Число называется гладким, если оно не имеет больших простых делителей.
Определение 4.2. Число называется 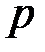 - гладким, если оно разлагается на простые множители, меньшие или равные
- гладким, если оно разлагается на простые множители, меньшие или равные  .
.
Алгоритм исчисления порядка состоит в следующем. Формируется множество базовых множителей

состоящее из первых 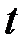 простых чисел.
простых чисел.
Задавая последовательно значения  1,2,3,…, находятся
1,2,3,…, находятся 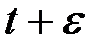 (
( - небольшое целое число)
- небольшое целое число)  -гладких чисел вида
-гладких чисел вида  , гладкость проверяется путем деления на элементы множества
, гладкость проверяется путем деления на элементы множества  . Каждое из
. Каждое из  -гладких чисел записывается через произведение базовых множителей
-гладких чисел записывается через произведение базовых множителей
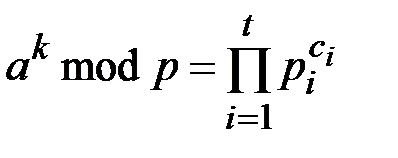 ,
,  . (4.3)
. (4.3)
Для каждого  получается свой набор
получается свой набор  .
.
Логарифмируем (4.3)
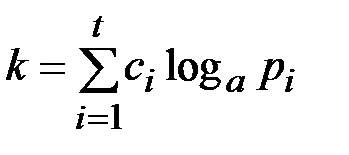 (4.4)
(4.4)
для каждого  -гладкого числа. Таким образом, получена система
-гладкого числа. Таким образом, получена система 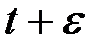 уравнений вида (4.3) с
уравнений вида (4.3) с  неизвестными. В качестве неизвестных выступают величины
неизвестными. В качестве неизвестных выступают величины 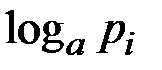 , при этом число уравнений на
, при этом число уравнений на 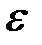 больше числа неизвестных, что повышает вероятность получения решения системы уравнений в случае, если некоторые уравнения окажутся линейно зависимыми.
больше числа неизвестных, что повышает вероятность получения решения системы уравнений в случае, если некоторые уравнения окажутся линейно зависимыми.
Решая систему уравнений все вычисления проводят по  . Напомним, что показатели степени, а следовательно и логарифмы, приводятся по
. Напомним, что показатели степени, а следовательно и логарифмы, приводятся по  . В результате получаем значения логарифмов чисел из множества
. В результате получаем значения логарифмов чисел из множества  :
:  ,
,  , …,
, …, 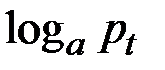 .
.
Случайным образом выбирается число 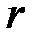 , находим
, находим  -гладкое число вида
-гладкое число вида 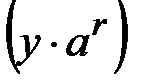
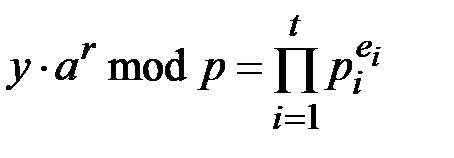 ,
,  . (4.5)
. (4.5)
Логарифмируя (4.5), получаем конечный результат

 . (4.6)
. (4.6)
Пример. Требуется решить уравнение  . Формируем множество базовых множителей
. Формируем множество базовых множителей 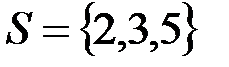 , тогда
, тогда  .
.
Пусть  , для простоты записи вводим обозначения
, для простоты записи вводим обозначения  ,
,  ,
, 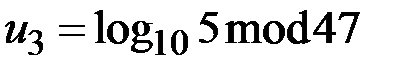 .
.
Проводим поиск  -гладких чисел
-гладких чисел
 ,
,
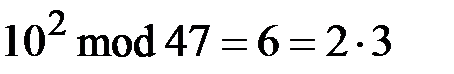 ,
,
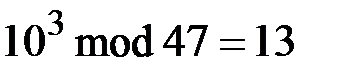 ,
,
 ,
,
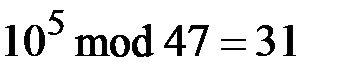 ,
,
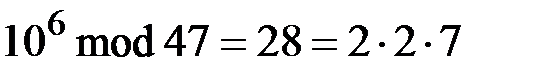 ,
,
 .
.
Значение 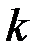 изменялось от 1 до 7. Дальнейший поиск
изменялось от 1 до 7. Дальнейший поиск  -гладких чисел не имеет смысла, т.к. определены
-гладких чисел не имеет смысла, т.к. определены 
 -гладких числа, соответствующие степеням 1,2,4 и 7.
-гладких числа, соответствующие степеням 1,2,4 и 7.
|
|
|
Прологарифмировав полученные уравнения и, с учетом введенных обозначений, имеем систему уравнений:

Исключая линейно зависимое уравнение и решая систему получаем
 ,
,
 ,
,
 .
.
Таким образом, в результате вычислений определены логарифмы чисел 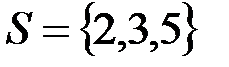 . В соответствии с (4.5), и начиная с
. В соответствии с (4.5), и начиная с 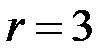 , вычисляем
, вычисляем
 ,
,
 .
.
В последнем равенстве переходим к логарифмам и получаем конечный результат
 .
.
Алгоритм Сильвера-Полига-Хеллмана. В 1978 году Полиг и Хеллман предложили алгоритм для решения задачи DPL. Суть алгоритма состоит в следующем [8].
Число  раскладывается на простые множители
раскладывается на простые множители
 ,
,
где 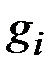 - различные простые числа,
- различные простые числа,  - натуральные числа.
- натуральные числа.
Затем составляется таблица 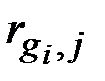 по правилу
по правилу
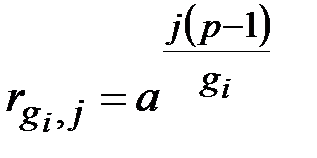
 ,
,  . (4.7)
. (4.7)
Аналогично алгоритму больших и малых шагов определяются отдельные дискретные логарифмы  . Для этого рассматривают представление
. Для этого рассматривают представление  по базе
по базе 
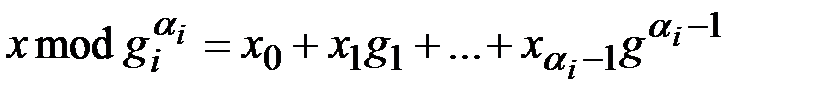 ,
, 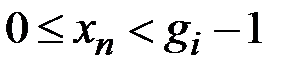 . (4.8)
. (4.8)
Для нахождения  вычисляется
вычисляется  , что эквивалентно
, что эквивалентно 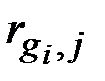 для некоторого
для некоторого  , и положить
, и положить  . Это возможно, т.к.
. Это возможно, т.к.
 .
.
Для нахождения  вычисляется
вычисляется 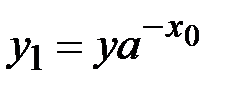 . Если
. Если
 ,
,
то  . Это возможно, т.к.
. Это возможно, т.к.
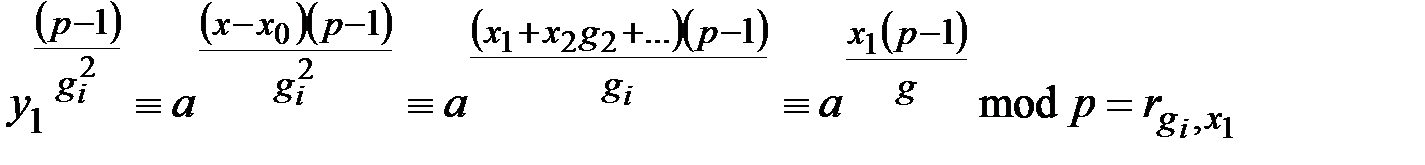 .
.
Для нахождения  вычисляется
вычисляется 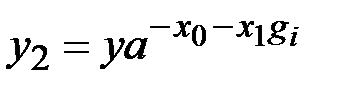 и
и  .
.
Таким же образом итеративно вычисляются  ,
,  , …,
, …,  . Далее, используя китайскую теорему об остатках, определяется значение
. Далее, используя китайскую теорему об остатках, определяется значение 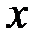 .
.
Пример. Требуется решить уравнение 
Разложим  на простые множители:
на простые множители: 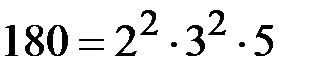 . Используя формулу (4.7) составляет таблицу.
. Используя формулу (4.7) составляет таблицу.
Вычисляем  для
для  :
:
 ,
,
 .
.
Вычисляем  для
для  :
:
 ,
,
 ,
,
 .
.
Вычисляем 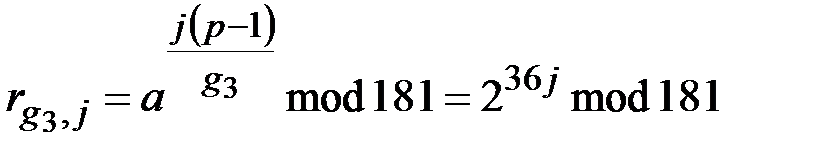 для
для  :
:
 ,
,
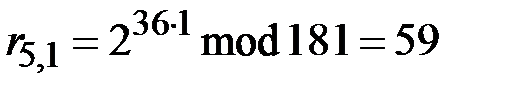 ,
,
 ,
,
 ,
,
 .
.
Таким образом, получаем таблицу (см. табл. 4.1).
Таблица 4.1
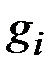
| 
| ||||
Составлять таблицу имеет смысл, только если все 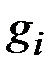 малы.
малы.
Затем определяем дискретные логарифмы  (4.8). Найдем дискретный логарифм
(4.8). Найдем дискретный логарифм  , то есть
, то есть  :
:
 .
.
Здесь  - символ эквивалентности.
- символ эквивалентности.
Для нахождения  вычислим
вычислим
 ,
,
следовательно,  .
.
Для нахождения  сначала вычисляем
сначала вычисляем  ., а затем
., а затем
 ,
,
следовательно,  .
.
Тогда  .
.
Аналогичным образом вычисляются дискретные логарифмы  и
и  .
.
В результате получаем систему уравнений
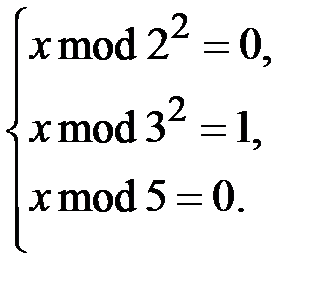
Решение системы уравнений находиться с помощью китайской теоремы об остатках. Системе удовлетворяет единственное решение  .
.
В настоящее время самым быстрым и эффективным алгоритмом решения задачи DPL является алгоритм NFS (Number Field Sieve). Именно этот алгоритм диктует условия выбора длин модулей криптосистем, стойкость которых основана на задаче DPL.
В табл. 4.2 приведены результаты сравнительного анализа трудоемкости решения задачи DPL.
Таблица 4.2. Трудоемкость решения задачи DPL.
| Метод | Трудоемкость |
| Полный перебор | 
|
| Метод больших и малых шагов | 
|
| Алгоритм исчисления порядка | 
|
| Алгоритм Сильвера-Полига-Хеллмана | 
|
Контрольные вопросы:
1. Назовите группы эффективных алгоритмов факторизации.
2. Опишите алгоритм Ферма. Какие требования он предъявляет к стойкости ассиметричных криптосистем?
3. Опишите  -метод Полларда. Какие требования он предъявляет к стойкости ассиметричных криптосистем?
-метод Полларда. Какие требования он предъявляет к стойкости ассиметричных криптосистем?
4. Назовите классы алгоритмов, которые используются для вычисления дискретного логарифма.
5. В чем суть метода больших и малых шагов?
6. Опишите алгоритм исчисления порядка. Дайте определение гладкости чисел.
7. Опишите алгоритм Сильвера-Полига-Хеллмана. Какие требования он предъявляет к стойкости ассиметричных криптосистем?
8. Проведите сравнительный анализ методов криптоанализа ассиметричных криптосистем.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 2065; Нарушение авторских прав?; Мы поможем в написании вашей работы!