Основные теоремы

Рассмотрим систему линейных уравнений

(1)

и соответствующую ей расширенную матрицу

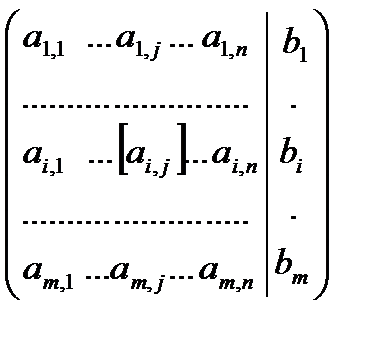(2)

Пусть все свободные члены в (1) (и, следовательно, в (2)) неотрицательны:

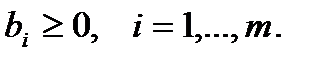(3)

Выделим некоторый, например, 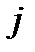-тый столбец, который далее будем называть ведущим.

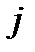Определение 1. Если элемент , стоящий в - той строке ведущего - того столбца матрицы системы (1), положителен, то определим для этой строки допустимое отношение 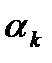, как отношение элемента столбца свободных членов к данному элементу ведущего столбца:

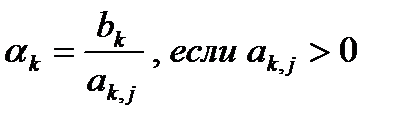, (4)

и положим

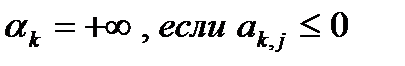. (5)

Определение 2. Строка с конечным минимальным допустимым отношением называется ведущей.

Определение 3. Элемент матрицы системы, стоящий на пересечении ведущей строки и ведущего столбца называется ключевым.

Пусть в нашем случае ведущей будет - тая строка. В матрице системы (2) ключевой элемент мы выделяем квадратными скобками. Ключевой элемент определяет одновременно ведущую строку и ведущий столбец. С помощью элементарных преобразований Гаусса, преобразуем матрицу системы (2) так, чтобы ведущий столбец стал базисным с единицей в ведущей строке. Для этого выполним следующую последовательность действий.

Вначале разделим ведущую строку на ключевой элемент. В результате получим ведущую строку вида:

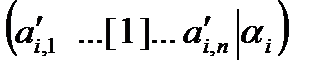(6)

Затем рассмотрим любую другую строку

(7)

с конечным допустимым отношением . Разделим строку (7) на соответствующий ей (положительный) элемент ведущего столбца . В результате в полученной строке в ведущем столбце будет стоять единица, а в столбце свободных членов – допустимое отношение этой строки:

. (8)

Из строки (8) вычтем ведущую строку (6). Получим строку:

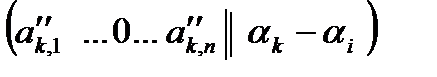. (9)

Поскольку - минимальное допустимое отношение, то свободный член полученной строки неотрицателен:

. (10)

Теперь рассмотрим строку с бесконечным допустимым отношением :

(11)

Чтобы в ведущем 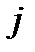- том столбце этой строки получить ноль, прибавим к ней ведущую строку, умноженную на число 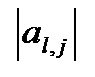. В результате получим строку вида:

. (12)

Ясно, что свободный член этой строки неотрицателен:

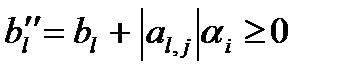, (13)

поскольку и .

В результате всех преобразований получим матрицу системы следующего вида

(14)

Как видно из вышеприведённых рассуждений, при этом окажется, что все свободные члены расширенной матрицы системы (14) также неотрицательны, если неотрицательны все свободные члены расширенной матрицы системы (2).

Таким образом, доказана следующая важная теорема.

Теорема о минимальном допустимом отношении. Пусть в расширенной матрице системы линейных уравнений с неотрицательным столбцом свободных членов выделен ведущий столбец и определена ведущая строка с минимальным допустимым отношением. Если с помощью элементарных преобразований Гаусса из исходной матрицы получена новая матрица, ведущий столбец которой является базисным с единицей в ведущей строке, то столбец свободных членов полученной матрицы будет также неотрицательным.

Из теоремы о минимальном допустимом отношении следует, что с помощью описанной в п.1.8 операции однократного замещения симплекс-таблица преобразуется в новую симплекс-таблицу.

Теорема об оптимальности опорного решения.

Пусть - опорное решение канонической задачи ЛП,

целевая функция зависит только от свободных переменных и все её коэффициенты отрицательны или равны нулю. Тогда - оптимальное решение этой задачи.

Доказательство. Без ограничения общности, можно считать свободными переменные 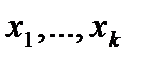. Тогда целевая функция имеет вид

(15)

и

. (16)

Из условия (16) и неотрицательности переменных 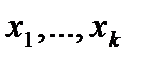следует, что для любого 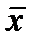из области допустимых решений справедливо неравенство:

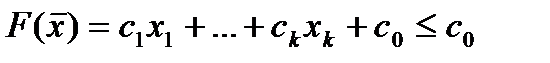. (17)

Поскольку все свободные переменные опорного решения равны нулю, то справедливо равенство:

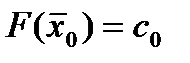, (18)

Из (17) и (18) следует, что - оптимальное решение. ч.т.д.

Замечание. Условие (16) равносильно тому, что все коэффициенты индексной строки симплекс-таблицы, кроме, быть может, свободного члена, неотрицательны.

Изложим теперь суть симплекс-метода (см. п.1.8-1.9). Исходным пунктом метода служит первая симплекс-таблица. Ей соответствует опорное решение (или угловая точка; см. п.1.9), оптимальность которого проверяется с помощью признака оптимальности. Если решение не оптимально, то выполняется операция однократного замещения, которая приводит к новой симплекс-таблице. Если алгоритм симплекс метода не останавливается (из-за невозможности выбора ведущей строки или возврата в одну из предыдущих угловых точек), через конечное число шагов будет найдено оптимальное решение. Это следует из того, что опорных решений конечное число.

Пусть на некотором шаге симплекс-метода в качестве ведущего выбран столбец свободной переменной 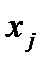(мы, как и раньше, будем предполагать, что свободными являются переменные 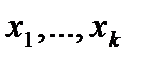). Предположим, что нельзя выбрать ведущую строку. Тогда в ведущем столбце симплекс-таблицы все коэффициенты отрицательны или равны нулю:

. (19)

Иначе, существовали бы минимальное допустимое отношение и соответствующая ему ведущая строка. Перенесём ведущий столбец в правую часть системы линейных ограничений:

Положив все свободные переменные, кроме 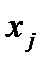, равными нулю получим систему:

(20)

В силу условий (3) и (19) система (20) определяет допустимое решение рассматриваемой задачи ЛП для любого неотрицательного значения переменной 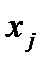. Поскольку целевая функция задачи зависит только от свободных переменных, из которых все, кроме переменной 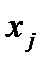, равны нулю, то:

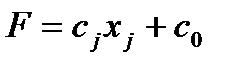
Так как для ведущего 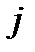- того столбца 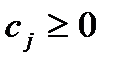, то:

.

Это доказывает, что соответствующая задача линейного программирования не имеет оптимального решения.

Подробно зацикливание, то есть возврат в одну из предыдущих угловых точек, мы обсуждать не будем. Отметим только, что при повторе ранее уже полученного опорного решения следует тем или иным способом изменить выбор ведущего столбца на текущем шаге. Например, можно на каждом шаге выбирать ведущий столбец случайным образом.

Из геометрической интерпретации задачи линейного программирования вытекает следующая теорема.

Теорема о достаточном условии существования оптимального решения задачи ЛП.

Если (многогранная) область допустимых решений задачи линейного программирования ограничена в направлении вектора роста целевой функции, то максимальное значение этой функции конечно и достигается в некоторой угловой точке ОДР.

Следствие. Если область допустимых решений задачи линейного программирования ограничена (является выпуклым многоугольником или многогранником), то оптимальное решение существует для любого вектора роста.

Дата добавления: 2014-12-26