ВВЕДЕНИЕ 3 страница

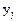
	0,50	0,72	0,94	1,16	1,38	1,60	1,82
	0,87	0,96	1,10	1,25	1,36	1,34	1,62

Каждая пара значений представляет координаты точки. Построив эти точки в системе координат xoy, по их расположению делаем вывод о виде функции регрессии. Из чертежа видно, что расположение точек близко к прямой линии, поэтому можно считать, что зависимость х на у является линейной.

Аналогично находим условные средние по формуле

; ;

;

;

;

;

;

.

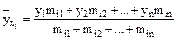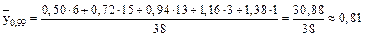Результаты вычислений поместим в табл.15.

Т а б л и ц а 15. Условные средние

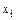
	0,57	0,78	0,99	1,20	1,41	1,62	1,83
	0,72	0,68	0,81	1,04	1,28	1,58	1,09

Точки 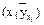построим на предыдущем чертеже и по их расположению делаем вывод о линейной зависимости у на х. Значит линии регрессии представляют собой прямые (рис.7).

3. Выборочный коэффициент корреляции находим по формуле

,

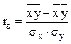где из расчетов задания 1 известно, что , , , .

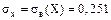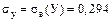Остается найти 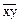. Воспользуемся корреляционной табл.13 и формулой

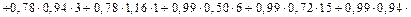
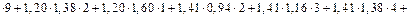
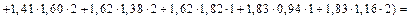
Рис. 7.

Выборочный коэффициент корреляции

По знаку 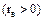и величине коэффициента корреляции делаем вывод о связи между СВ X и У: прямая линейная корреляционная зависимость, средняя связь.

Квадрат коэффициента корреляции называется коэффициентом детерминации, который показывает процент влияния СВ X на СВ У.

В нашем случае коэффициент детерминации равен

.

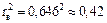Вывод: примерно 42% составляет влияние стоимости основных производственных фондов на стоимость валовой продукции. Остальные 58% обусловлены влиянием других факторов.

4. Доверительный интервал для коэффициента корреляции генеральной совокупности с заданной доверительной вероятностью находится по формуле

где 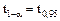находится, используя функцию Лапласа: , т.е. 0,95=Ф(t_0,95). По значению функции Лапласа 0,95, по приложению 1 находим значение t_0,95 = 1,96.

Подставим имеющиеся данные в формулу доверительного интервала: имеем .

В результате вычислений получим доверительный интервал .

Вывод: если рассматривать большое число выборок системы СВ Х и У и для каждой из них найти коэффициент корреляции , то примерно в 95% из них доверительный интервал накроет коэффициент корреляции генеральной совокупности и только в 5% случаев может выйти за границы этого интервала.

5. Найдем линейные уравнения функций регрессии. Уравнение регрессии у на х имеет вид: Подставляем имеющиеся данные: имеем

преобразуя, получим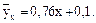

Аналогично составим уравнение регрессии x на y.

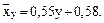
Построим эти прямые на чертеже (рис.7), учитывая, что они проходят через точку

Задание 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

На основании опытных данных х и у требуется:

1) построить точки и по точечной диаграмме определить вид эмпирической функции;

2) найти параметры эмпирической функции методом наименьших квадратов;

3) построить график эмпирической функции на точечной диаграмме;

4) выполнить эту работу на ЭВМ.

Решение типового варианта

Методику выполнения этого задания покажем на примере опытных данных, приведенных в табл. 16, где х– количество внесенных удобрений определенного вида на 1 га; у – урожайность ячменя, ц/га.

Т а б л и ц а 16. Опытные данные урожайности

Дата добавления: 2014-12-23