
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад виконання задачі 9
|
|
|
|
Зобразити розрахункову схему в аксонометрії. Побудувати окремо епюри згинальних і крутних моментів та визначити діаметри ділянок стержня за третьою теорією міцності, якщо МПа.
На рисунках 1.22 – 1.23 зображено в аксонометрії вісь ламаного стержня круглого поперечного перерізу, розташованого в горизонтальній площині. На стержень діє вертикальне навантаження.
Завдання до розрахунково-графічної роботи
Задача 9. Розрахунок плоскої рами з просторовим навантаженням
Дані взяти з таблиці 1.4.
Таблиця 1.4
| № варіанта | Р, кН | q, кН/м | a, м | b, м | c, м |
| 0,5 | 1,2 | ||||
| 1,2 | 0,5 | ||||
| 1,2 | 0,5 | ||||
| 0,8 | 0,6 | ||||
| 0,5 | 0,8 | ||||
| 0,5 | |||||
| 0,5 | 0,8 | ||||
| 0,6 | 1,2 | ||||
| 0,4 | 0,8 | ||||
Для просторової рами, що навантажена згідно зі схемою (рис. 1.24) побудувати епюри внутрішніх зусиль та визначити необхідні діаметри поперечних перерізів ділянок за третьою теорією міцності.
Дано:
P = 8 кН; q = 6 кН/м;
a = 1 м; b = 0,6 м; c = 1,2 м;
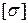 = 160 МПа.
= 160 МПа.
Знайти:
dі -?
1. Будуємо епюри внутрішніх зусиль
Перерізи вибираємо таким чином, щоб розглядати консольну частину рами так як показано на рис. 1.25. Для кожного перерізу вказуємо локальну систему координат таким чином, щоб вісь х збігалася з віссю ділянки та була направлена до частини стержня, що розглядається. Вісь у направляємо вертикально, вісь z утворює праву систему координат. Таким чином, моменти зовнішніх сил відносно осі х будуть крутними моментами, відносно осі у – згинальними моментами в горизонтальній площині, відносно осі z – в вертикальній площині.

Рисунок 1.22 - Схеми до виконання задачі 9
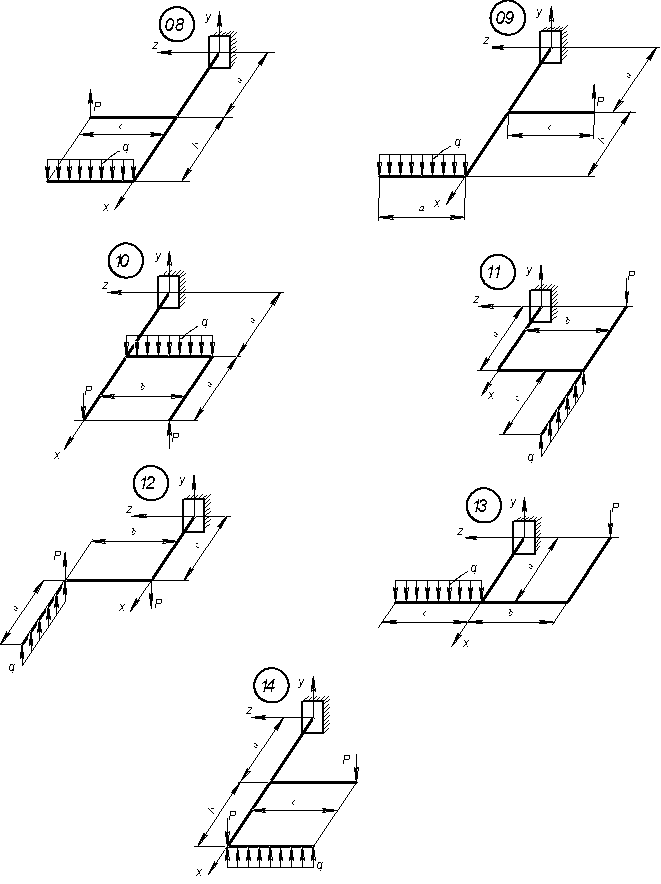
Рисунок 1.23 - Схеми до виконання задачі 9

Рисунок 1.24 - Схема до прикладу задачі 9
Розв’язування
Оскільки навантаження на раму вертикальне, то поперечні сили і згинальні моменти (епюри) будуть лежати в вертикальній площині xoy.
Поздовжні сили при такому навантаженні в рамі не будуть виникати.
Запишемо для кожної ділянки рівняння поперечних сил, згинальних та крутних моментів.
Ділянка АВ:
 м
м
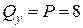 (кН),
(кН),
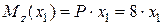 ,
,
при  (м)
(м)  (кН×м),
(кН×м),
при 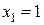 (м)
(м) 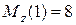 (кН×м).
(кН×м).
Ділянка ВE:
 м
м
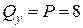 (кН),
(кН),
 (кН×м),
(кН×м),
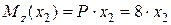 ,
,
при  (м)
(м)  (кН×м),
(кН×м),
при  (м)
(м)  (кН×м).
(кН×м).
Ділянка CD:
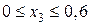 м
м
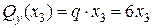 (кН),
(кН),
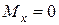 (кН×м),
(кН×м),
 ,
,
при  (м)
(м)  (кН),
(кН),
 (кН×м),
(кН×м),
при 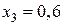 (м)
(м) 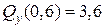 (кН),
(кН),
 (кН×м).
(кН×м).
Ділянка DE:
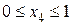 м
м
 (кН),
(кН),
 (кН×м),
(кН×м),
 ,
,
при  (м)
(м)  (кН×м),
(кН×м),
при 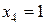 (м)
(м) 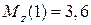 (кН×м).
(кН×м).
Ділянка DE:
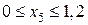 м
м
 (кН),
(кН),
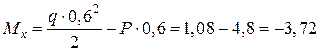 (кН×м),
(кН×м),
 ,
,
при  (м)
(м)  (кН×м),
(кН×м),
при 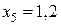 (м)
(м) 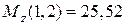 (кН×м).
(кН×м).
Для всіх ділянок  ,
,  ,
, 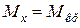 ,
,  .
.
За отриманими значеннями будуємо епюри в аксонометрії (рис. 1.26).
Епюри згинальних моментів відкладаємо на розтягнутих волокнах. Розташування епюр крутних моментів особливого значення не має. Додатні значення поперечної сили відкладені над віссю.
2. Розрахунок на міцність
Впливом поперечних сил нехтуємо.
За третьою теорією міцності (найбільших дотичних напружень)

Визначаємо максимальні значення зведених моментів в відповідних точках кожної ділянки
АВ: т. В:  (кН×м).
(кН×м).
ВЕ: т. Е.  (кН×м).
(кН×м).
CD: т. D: 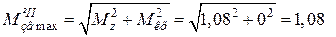 (кН×м).
(кН×м).
DE: т. E: 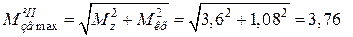 (кН×м).
(кН×м).
EF: т. F: 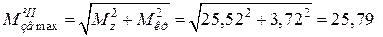 (кН×м).
(кН×м).
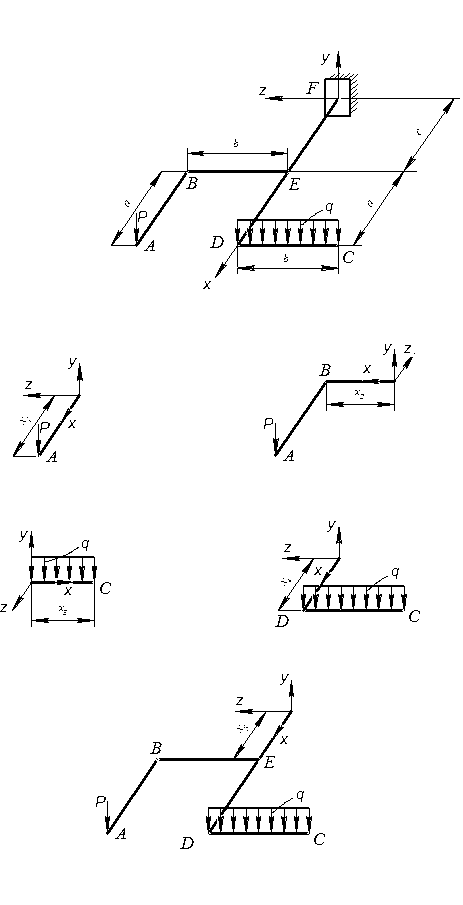
Рисунок 1.25 - Характерні перерізи на розрахункових ділянках
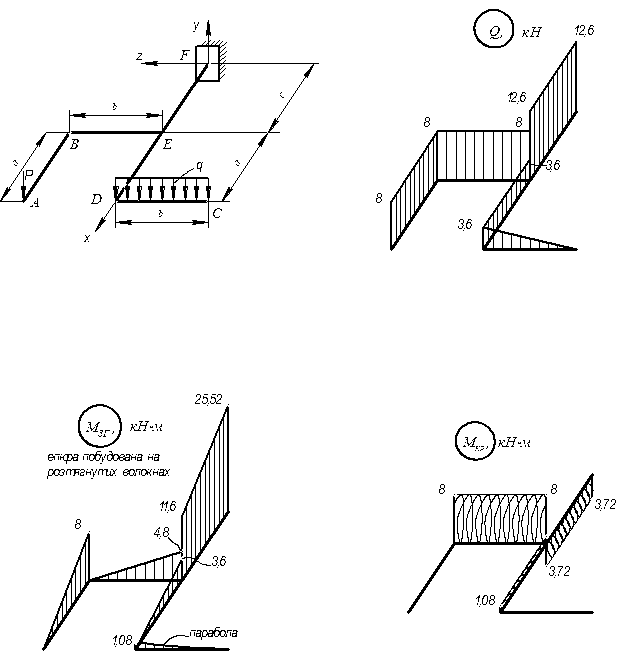
Рисунок 1.26 - Епюри внутрішніх зусиль
Розраховуємо мінімальні діаметри ділянок вала за умовою міцності при згині з крученням.
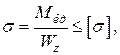
де  - осьовий момент опору круга, звідки
- осьовий момент опору круга, звідки

Ділянка АВ:
 (м).
(м).
ВЕ:  (м).
(м).
CD:  (м).
(м).
DE:  (м).
(м).
EF:  (м).
(м).
Округлюємо отримані значення до стандартних (додаток К, ряд Rа 40) та остаточно приймаємо  = 80 мм,
= 80 мм, 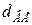 = 85 мм,
= 85 мм,  = 42 мм,
= 42 мм, 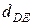 = 63 мм,
= 63 мм, 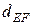 = 120 мм.
= 120 мм.
Відповідь:  = 80 мм,
= 80 мм, 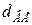 = 85 мм,
= 85 мм,  = 42 мм,
= 42 мм, 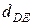 = 63 мм,
= 63 мм, 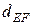 = = 120 мм.
= = 120 мм.
Питання до захисту розрахунково-графічної роботи (задачі 8, 9)
1. Записати умову міцності при згині з крученням та пояснити її.
2. Що таке зведений момент та як він визначається за третьою та четвертою теоріями міцності?
3. Визначити максимальне еквівалентне напруження у вказаному перерізі вала (рами).
4. В яких елементах конструкцій реалізуються деформації згину з крученням? Навести приклади.
5. Побудувати епюри розподілу нормальних та дотичних напружень у вказаному перерізі вала.
6. За якою залежністю визначається необхідний діаметр вала (рами) при згині з крученням?
7. За яким алгоритмом виконують розрахунки вала при згині з крученням?
8. Які епюри внутрішніх зусиль вказують на згин з крученням? Які епюри не використовуються в розрахунку і чому?
9. Чому для вала будують епюри в двох розрахункових площинах – вертикальні та горизонтальні? Чи має значення саме такий вибір площин?
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 611; Нарушение авторских прав?; Мы поможем в написании вашей работы!